Теория размерностей и фракционный анализ, страница 3

         Независимыми переменными являются величины, необходимые для однозначного определения состояния системы.

         Параметры – величины, имеющие конкретное численное значение для рассматриваемой задачи и изменяющие при переходе к другим однотипным задачам.

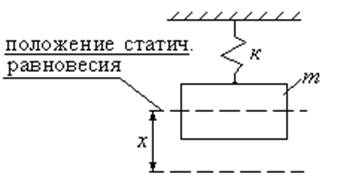
         Зависимая искомая величина является функцией как независимых, так и параметров. В примере независимая переменная времени, m и k – параметра, а отклонение есть зависимая переменная. Для всех однотипных рассмотренной системы  отклонение есть функция времени и параметров.

         Бриджмен показал, что анализ размерностей применим лишь к тем задачам и уравнениям, которые в безразмерном виде однородны и связаны с основными системами единиц. У таких задач структура формулы не зависят от величины единицы, принятой в качестве основной.

         Всегда решая задачу, удобнее заменять размерные величины, в том числе и результат в безразмерной форме. Это приводит к снижению числа необходимых независимых координат и уменьшению требуемого числа – данных, графиков, экспериментов и таблиц. Кроме того, безразмерная форма облегчает сопоставление и обобщение результатов.

2.2. Единицы измерений и размерности

         Под единицами измерения будем понимать меры, с помощью которых измеряются величины физико-технических характеристик системы. Для измерения как конкретной операции необходимо иметь:

1. базовую величину или начало отсчета;

2. единицу измерения, определяемую с помощью рабочей операции;

3. правила интерполяции и экстраполяции.

Допустим, нам необходимо измерить длину стального стержня. В этом случае базовая величина принимается равной нулю. Единицей измерения является метр. Правило интерполяции позволяет нам наносить его произвольные части путем маркировки на делительных машинах. Размерности по своей сути являются относительными величинами, они зависят от специфики рабочих операций, используемых в процессе измерения. В математическое описание физических процессов входят четыре типа характеристик:

1. первичные величины;

2. вторичные величины;

3. размерные постоянные;

4. безразмерные величины.

         Первичной величиной называется любая величина, размерность которой пропорциональна первой степени единицы измерения, определенной с помощью выбранной рабочей операции. При этом не должны использоваться две рабочих операции или выражения, имеющие размерности в отличной от единицы степени.

         Длина стержня – первичная величина. Ее размерность  []. Площадь поперечного сечения стержня не первичная величина, так как она выражается квадратом длины [²].

         Для измерения скорости, например летящего самолета, мы должны добавить вторую рабочую операцию, связанную с измерением времени. Следовательно, скорость тоже не может считаться первичной величиной. Такие величины как скорость и площадь будем называть вторичными. В физике их подразделяют на основные и производные. Размерность вторичных величин можно выразить лишь единственной комбинацией размерностей первичных величин в различных степенях. Возьмем символ А – заменяющий слова имеет размерность (или единицу измерения). Размерность любой вторичной величины можно выразить формулой размерности

,

где  – температуры,  – массы,  – длины,  – времени.

                                                                                                                        Таблица 1.