Основные понятия и законы электрических цепей

ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

1.1. Определение электрической цепи

Общее определение электрической цепи (ЭЦ). Совокупность элементов и устройств, образующих путь для электрического тока, электромагнитные процессы в которой могут быть описаны с помощью понятий электродвижущей силы, тока и напряжения, называется электрической цепью.

Формальное определение ЭЦ.С формальной точки зрения  ЭЦ содержит три множества объектов

C = (K, B, N),

где K = {k₁, k₂, ... , k_n} —  множество  компонентов цепи; В = {b₁, b₂, ... , b_m} — множество ветвей цепи;

N = {n₁, n₂, ... , n_k} — множество узлов цепи.

Компоненты цепи делятся на две группы: источники электрической энергии и приемники.

К источникам электрической энергии (первичным источникам) относятся различные устройства, в которых происходит преобразование химической, тепловой, механической и других видов энергии в электрическую. Примеры —  аккумуляторы, батареи, гидрогенераторы.

Приемники электрической энергии — это компоненты ЭЦ, в которых происходит преобразование электрической энергии в другие виды энергии, а также аккумулирование электрической энергии. Примеры — резисторы, диоды, электродвигатели и другие.

1.2. Топологические характеристики цепи

Каждый компонент цепи может иметь произвольное число выводов (связей). Выводы компонентов заканчиваются зажимами или полюсами. Соответственно компоненты

(рис. 1.1, а) называются многополюсниками, а компоненты (рис. 1.1, б) — двухполюсниками. Примерами многополюсников являются транзисторы, трансформаторы, а примерами двухполюсников —  диоды, резисторы, индуктивности. Любая часть электрической цепи, имеющая два зажима (полюса), называется двухполюсником. Двухполюсник имеет  условное изображение в виде прямоугольника с двумя выводами. Различают активные (А) и пассивные (П) двухполюсники (рис. 1.1, в).

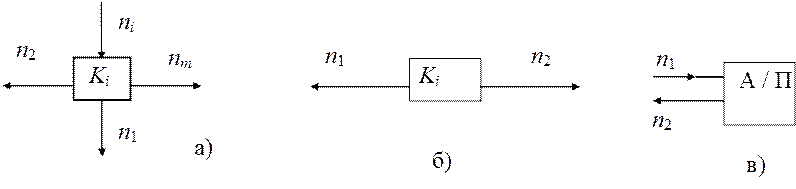
Рис. 1.1

Выводы компонентов при включении их в цепь образуют ветви и узлы цепи. Точки объединения связей компонентов образуют множество узлов цепи. Ветвью может быть назван любой участок цепи, заключенный между двумя узлами при условии равенства токов на его входе и выходе (рис.1.2, а, б), т. е. i₁ = i_2.. Ряд двухполюсных компонентов имеет два вывода, но при включении в цепь характеризуются одной ветвью. Примером здесь служат резисторы, емкости, индуктивности, диоды и пр. Электрическая цепь в общем случае содержит n компонентов, m ветвей и k узлов.

Рис. 1.2

Ветвь может содержать произвольное число последовательно соединенных компонентов: сопротивлений, конденсаторов, катушек, источников ЭДС. Если через все эти компоненты проходит один и тот же ток, то такое соединение будем называть последовательным. Параллельным соединением компонентов (ветвей) электрической цепи называют соединение, при котором все участки цепи присоединяются к одной и той же паре узлов с одинаковым напряжением. Смешанное соединение предполагает сочетание последовательного и параллельного соединений. Более сложные электрические цепи  могут не сводиться к последовательному  и параллельному соединениям.

Топологические свойства электрических схем не зависят от типа и свойств элементов, из которых они составлены. Поэтому исследование топологических свойств цепей удобно проводить на основе теории графов.

Графом электрической схемы называют ее условное графическое отображение, в котором ветви схемы представлены отрезками, а узлы — точками. Отрезки линий, соответствующие ветвям схемы, называют ветвями (ребрами) графа, а концевые точки ветвей — узлами (вершинами) графа. Графы могут быть направленными и ненаправленными. Направленным называют граф, в котором указаны условно-положительные направления его ветвей, в противном случае граф называют ненаправленным. Если между любой парой узлов графа можно указать путь (непрерывную последовательность ветвей), то такой граф называют  связным.

Важным является понятие  подграфа — любое множество ветвей и узлов, содержащихся в данном графе.

В теории цепей большое значение имеют такие подграфы: путь, контур, дерево, связь  и сечение.

Контур — замкнутый путь графа, в котором один из узлов графа является начальным и одновременно конечным.

Деревом связного графа называют связный подграф, содержащий любую совокупность ветвей связного  графа, соединяющих все его узлы, но не образующих ни одного контура.

Ветви графа, не входящие в число ветвей дерева, называют связями.

Сечением графа называют минимальную совокупность его ветвей, при удалении которых граф распадается на два несвязных графа. Изображают сечение в виде замкнутой линии (поверхности), которая один раз пересекает каждую ветвь этой совокупности.

Приведенные определения показывают, что в любой относительно сложной схеме имеется большое число  различных путей, деревьев, связей контуров и сечений. Однако в теории цепей существенную роль играют не все контуры и сечения, только главные.

Главным называют контур, состоящий из любого числа ветвей дерева и только одной ветви связи. Главным сечением называют такое, в которое входит любое число ветвей связи и только одна ветвь дерева. Как будет показано ниже, на основе главных контуров и сечений могут быть составлены независимые уравнения для анализа схем.

Для схемы направленного графа (содержащего ветви 1 — 6) главные контуры I, II, III (рис. 1.3, а) и сечения S₁, S₂, S₃ (рис. 1.3, б) могут быть построены на основе одного дерева, включающего ветви 1, 4, 5, выделенные жирными линиями (рис. 1.3, а,  б). Направления ветвей, главных контуров и сечений графа выбираются произвольно.

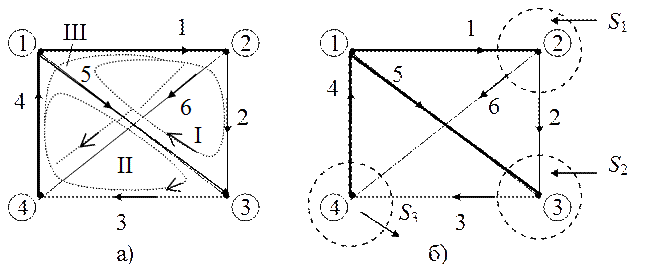
Рис. 1.3

Аналитически информацию о графе удобно представлять в матричной форме. В матрице ненаправленного графа перечисляются все его узлы и ветви, а также содержится информация о том, между какими узлами находятся соответствующие ветви. При матричном описании направленных графов необходимо также указать и направление каждой ветви. Графы описывают узловыми, контурными матрицами и матрицами сечений.

Узловой матрицей A направленного графа называют прямоугольную матрицу с числом строк, равным числу узлов без единицы и числом столбцов, равным числу ветвей графа. Каждый элемент a_ij такой матрицы определяется по правилу

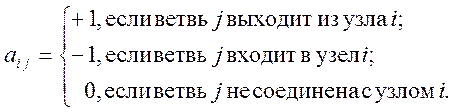
Для одного из узлов графа матрицу не заполняют. Такой узел называют опорным или базисным.

Для направленного графа (рис. 1.3) узловая матрица имеет вид:

Контурной матрицей В направленного графа называют прямоугольную матрицу с числом строк, равным числу контуров графа и числом столбцов, равным числу его ветвей. Каждый элемент b _{i j} матрицы определяется по правилу

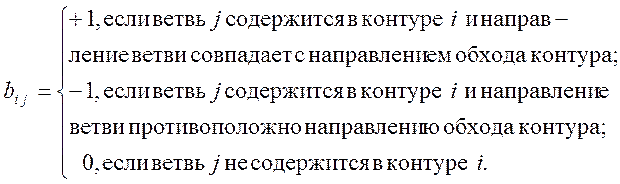
Матрица главных контуров для графа (рис. 1.3) имеет вид: