Основные понятия и законы электрических цепей, страница 5

Закон Ома выражает связь между током и напряжением. Например, ток ветви с резистором связан с напряжением на резисторе уравнением 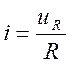. Уравнения закона Ома для емкости и индуктивности можно найти в табл. 1.1.

Топологические уравнения отражают свойства цепи, которые определяются только ее топологией и не зависят от того, какие компоненты входят в состав ветвей. К топологическим уравнениям относятся, в частности, уравнения, составленные на основании первого и второго законов Кирхгофа.

Первый закон Кирхгофа. Алгебраическая сумма мгновенных значений токов всех ветвей, соединенных  в каждом из узлов (либо протекающих через любое сечение) моделируемой цепи, в любой момент времени равна нулю: 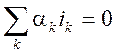, где   — знаковый коэффициент.  для токов, ориентированных к узлу (сечению);  для токов, ориентированных от узла (сечения); k — номер ветви, подключаемой к рассматриваемому узлу. 

Второй закон Кирхгофа. Алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур моделируемой цепи, в каждый момент времени равна нулю: 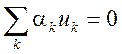, где k — номер ветви, входящей в рассматриваемый контур;  — знаковый коэффициент, который равен +1, если положительное направление напряжения ветви совпадает с направлением обхода контура.

Другая форма второго закона Кирхгофа. Алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур моделируемой цепи, в каждый момент времени равна алгебраической сумме мгновенных значений ЭДС источников напряжения, действующих в этом контуре: 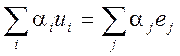. Знаковые коэффициенты равны +1, если направление  или совпадает с направлением обхода контура.

1.8. Модели электрической цепи.

Анализ и синтез электрических цепей

Любую ЭЦ можно рассматривать как систему (С), имеющую множество внутренних параметров

Р = {р₁, р₂, ... , р_q},

множество входов

Х = ={x₁, x₂, ... , x_m}

и множество выходов

Y = {y₁, y₂, ... , y_n},

где m и n — соответственно число входов и выходов (рис. 1.16).

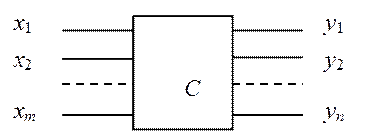
Рис. 1.16

Электрическая цепь может быть объявлена составной частью другой ЭЦ либо компонентом с m + n полюсами.

В зависимости от исходных данных и конечной цели моделирования в теории цепей различают две группы задач — задачи анализа и задачи синтеза.

Задача анализа ЭЦ состоит в определении реакции цепи Y на заданные внешние воздействия при известных внутренних параметрах Р (называемых также характеристиками ЭЦ):  Y = f (X, P).

Задача синтеза ЭЦ заключается в нахождении структуры С и параметров Р цепи по заданной реакции Y на некоторые внешние воздействия Х.

Математически задача анализа ЭЦ сводится к составлению и решению системы линейно независимых уравнений, переменными которых являются токи и напряжения ветвей. Совокупность уравнений (соотношений), решение которых позволяет определить токи и напряжения ветвей ЭЦ, называется моделью электрической цепи. Очевидно, что число уравнений модели ЭЦ должно равняться количеству неизвестных токов и напряжений.

Решением электрической цепи называется вектор неизвестных цепи V = [v, i]^T, где vи i — напряжения и токи ветвей, также векторные величины; [v, i]^T — транспонированная матрица этих величин.

В общем случае в цепи, содержащей m ветвей и k узлов, имеется 2m неизвестных токов и напряжений ветвей. Используя первый закон Кирхгофа, можно составить k – 1 независимых уравнений баланса токов и m – k + 1 уравнений баланса напряжений по второму закону Кирхгофа. В сочетании с компонентными уравнениями (уравнениями ветвей) получаем 2m линейно независимых уравнений модели цепи, которых достаточно для ее корректного расчета.

Таким образом, используя компонентные уравнения и топологические уравнения, составленные по законам Кирхгофа, всегда можно построить модель цепи, в которой число уравнений является достаточным для определения всех неизвестных токов и напряжений. 

На практике для анализа цепей используют различные методы составления моделей ЭЦ. Эти методы различаются прежде всего вектором независимых переменных и базируются на использовании различных приемов, позволяющих уменьшить размерность вектора неизвестных цепи. Приведем примеры вектора решения для наиболее известных методов. Метод контурных токов: V = [j₁, j₂, … , j_p]^T,где j — токи контуров; р — число контуров ЭЦ. Метод узловых напряжений: V = [u₁, u₂, ... , u_{k - 1}]^T, где u — напряжения узлов; (k– 1) — число узлов цепи, исключая базовый. Табличный метод: V = [u₁, u₂, ... , u_{k - 1,} i_1, i₂, ... , i_m]^T, где u — напряжения узлов размерности (k – 1); i — токи ветвей размерности m.

1.9. Классификация электрических цепей

Электрические цепи, составленные из идеализированных элементов, могут быть классифицированы по ряду признаков. По топологическим особенностям: простейшие (одноконтурные, двухузловые) и сложные (многоконтурные, многоузловые). По числу внешних выводов компонентов (двухполюсники, многополюсники и др.). По энергетическим свойствам: активные (содержащие источники энергии) и пассивные (не содержащие источников). По типу параметров (сосредоточенные, распределенные), по характеру процессов (непрерывные, дискретные, непериодические и пр.).

Фундаментальный характер имеет классификация цепей в зависимости от типа уравнений модели цепи. В свою очередь тип модели цепи определяется типами уравнений (моделей) входящих в нее компонентов. В соответствии с этим можно выделить: линейные статические модели постоянного тока (линейные алгебраические уравнения); линейные инерционные модели  во временной области (линейные дифференциальные уравнения)  и в частотной области (линейные алгебраические уравнения); нелинейные статические модели (нелинейные алгебраические уравнения); нелинейные инерционные модели (нелинейные алгебро-дифференциальные уравнения).