Рассмотрим четыре формы сигналов источников. Постоянный сигнал: e(t) = E = const (рис. 1.9, кривая 1). Гармонический сигнал: e(t) = Em sin(wt+j0) (рис. 1.9, кривая 2). Периодический негармонический сигнал, описывается рядом Фурье (рис. 1.9, кривая 3). Непериодический сигнал, описывается интегралом Фурье (рис. 1.9, кривая 4).
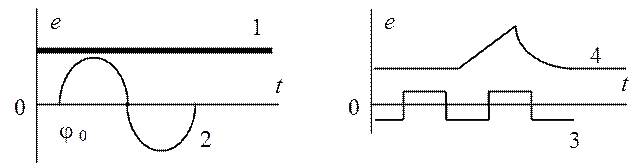
Рис. 1.9
Управляемые источники тока и напряжения. Идеальные источники тока и напряжения могут быть и управляемыми (зависимыми). В общем случае управляемый источник — это идеализированный активный элемент с двумя парами выводов, параметр которого является определенной функцией тока или напряжения некоторого участка цепи.
Внутреннее сопротивление управляемого источника напряжения равно нулю, а внутреннее сопротивление управляемого источника тока равно бесконечности.
Источник напряжения, управляемый напряжением (ИНУН), показан на рис. 1.10, а. Уравнения ИНУН:
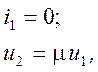
где m — коэффициент передачи по напряжению.
Источник напряжения, управляемый током (ИНУТ), показан на рис. 1.10, б. Уравнения ИНУТ:
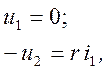
где r — передаточное сопротивление.
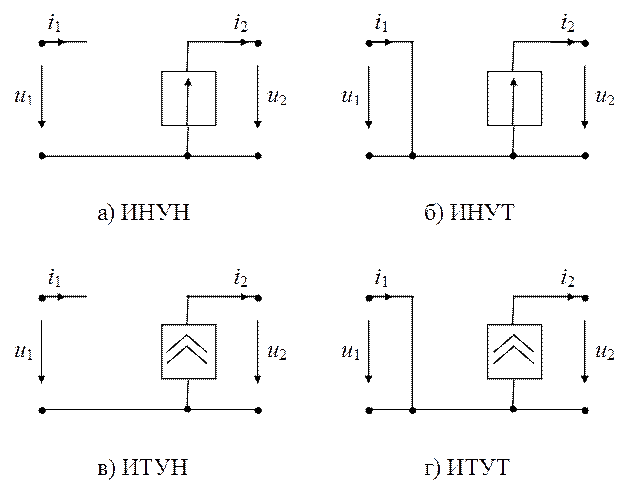
Рис. 1.10
Источник тока, управляемый напряжением (ИТУН), показан на рис. 1.10, в. Уравнения ИТУН:
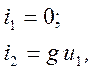
где g — передаточная проводимость.
Источник тока, управляемый током (ИТУТ), представлен на рис. 1.10, г и описывается уравнениями:
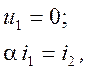
где a — коэффициент передачи по напряжению.
Приведенные управляемые источники являются линейно управляемыми, хотя в общем случае зависимости между током и напряжением могут быть произвольной формы. Управляемые источники тока и напряжения широко используют при составлении эквивалентных схем электронных приборов.
1.6. Классификация сигналов
Одномерные и многомерные сигналы. Типичным примером сигнала является напряжение на зажимах (входных или выходных) какой-либо цепи. Такой сигнал описывается одной функцией времени и называется одномерным (например, напряжение u (t) на зажимах вольтметра (рис. 1.11, а).
Многомерный сигнал образуется как множество одномерных 
,
где n — размерность сигнала (рис. 1.11, б).
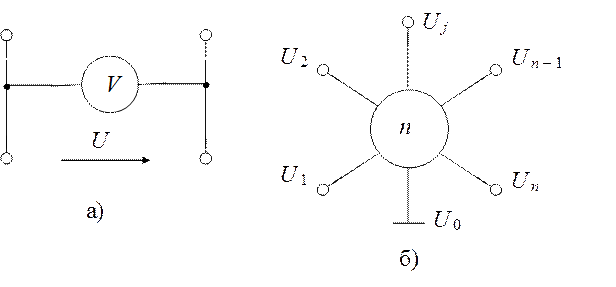
Рис. 1.11
Детерминированные и случайные сигналы. Детерминированный сигнал — это сигнал, математическая модель которого позволяет предсказать его мгновенное значение в любой момент времени, например:
; 
,
где
— круговая частота, T
— период.
Случайный сигнал — это, как правило, помехи, препятствующие получению полезного сигнала из принятого сообщения, вызванные различными флуктуациями (тепловыми, электромагнитными и др.).
В физическом смысле чисто детерминированных сигналов не существует. Любой сигнал содержит в своем составе случайную по времени составляющую (помеху), и часто эти составляющие соизмеримы по величине.
Импульсные сигналы. Импульсные сигналы — это сигналы, существующие лишь в пределах конечных отрезков времени. Они могут следовать во времени с некоторой частотой повторения, либо быть одиночными.
Различают видеоимпульсы (рис. 1.12, а) и радиоимпульсы
(рис. 1.12, б). Радиоимпульс представляет собой некоторую несущую
частоту 
, промодулированную видеоимпульсом.
Радиоимпульс 
и видеоимпульс 
связаны соотношением
.
При
этом функцию называют огибающей, а функцию 
— заполнением.
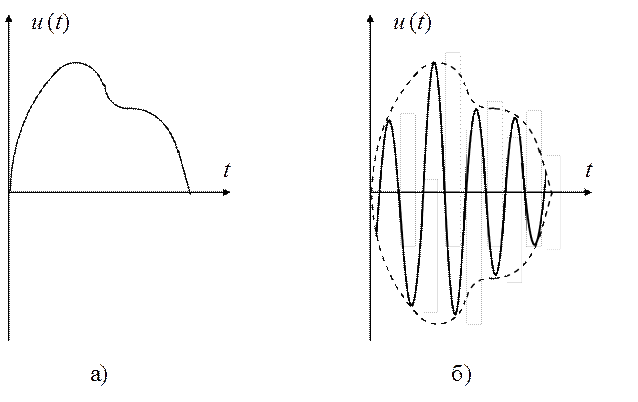
Рис. 1.12
В современной электронике длительность импульсов колеблется от нескольких секунд до долей наносекунды.
Аналоговые, дискретные и цифровые сигналы. Сигнал, который полностью аналогичен протекающему физическому процессу и который может быть измерен в любой момент времени, называется аналоговым сигналом. Одномерный аналоговый сигнал представляет собой осциллограмму, график которой может быть задан непрерывным (рис. 1.13, а) или дискретным (рис. 1.13, б) способом.
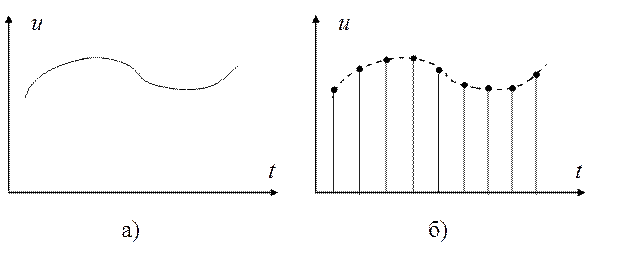
Рис. 1.13
Дискретный сигнал представляет собой счетное множество точек на оси времени, в каждой из
которых определено отсчетное значение сигнала 
.
При этом шаг дискретизации 
— постоянный,
постоянна и ширина (длительность) 
отдельного
импульса. Тогда площадь импульса несет информацию о значении сигнала в данной
точке. Очевидно, что при этом 
, а частота
дискретного сигнала 
много больше частоты
аналогового сигнала 
.
Основное достоинство аналогового дискретизированного сигнала состоит в том, что при его воспроизведении достаточно иметь информацию о значениях функции в точках дискретизации и интерполировать остальные значения, что позволяет по одному каналу одновременно передавать большое количество сигналов, используя режим разделения времени.
Однако рассмотренный принцип дискретизации сигнала трудно реализуется физически и сильно зависит от помех при обработке сигнала.
Поскольку информация заключается в площади дискретного импульса, то можно сделать амплитуду импульса постоянной, а длительность поставить в соответствие значению сигнала (рис. 1.14). Это — второй способ дискретизации сигнала.
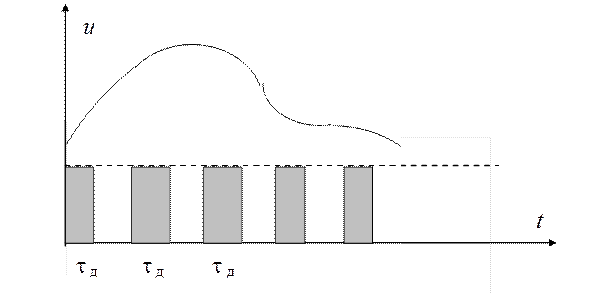
Рис. 1.14
Значение величины сигнала в точках отсчета для обоих способов дискретизации может быть представлено в цифровой форме, например, в двоичной системе счисления. Поскольку цифровая форма записи двоичного числа — это последовательность единиц и нулей, то физическая реализация этой формы выглядит как импульсные сигналы фиксированной частоты и длительности двух уровней, один из которых соответствует единице, а другой — нулю (рис. 1.15).
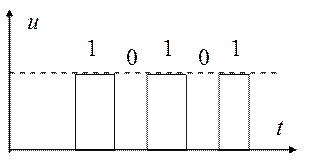
Рис. 1.15
Для осуществления операции представления аналогового сигнала в цифровой форме и для обратного преобразования соответственно разработаны микросхемы аналого-цифровых (АЦП) и цифро-аналоговых (ЦАП) преобразователей.
1.7. Понятие о компонентных и топологических уравнениях. Закон Ома. Законы Кирхгофа
Математическое описание процессов в электрических цепях базируется на компонентных и топологических уравнениях.
Компонентные уравнения (уравнения компонентов или ветвей) устанавливают связь между током и напряжением каждой ветви в ЭЦ. Количество таких уравнений равно числу ветвей, а вид уравнений зависит от типа рассматриваемого компонента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.