Обоснование выбора закона распределения вероятностей, описывающего поведение случайной величины. Выписать аналитический вид кривой функции распределения вероятности соответствующего закона распределения

Московский энергетический институт (Технический университет)

Типовой расчет
по предмету: «Статистические методы»

Вариант №4

Выполнил
 студент группы А-01-03

Козлов Максим Алексеевич

Москва 2005 г.

Постановка задачи

Локальная сеть ЭВМ обеспечивает работу 15 терминалов. Пользователи, решающие задачи различной сложности обращаются к серверу в случайные моменты времени. Интервал времени между обращениями является случайной величиной Y.

Задание:

1.  Обосновать выбор закона распределения вероятностей, описывающего поведение случайной величины;

2.  Выписать аналитический вид кривой функции распределения вероятности соответствующего закона распределения;

3.  Задавшись значениями параметров кривой f(y,θ) (θ = (θ₁,…,θ_k)), образовать 100 значений случайной величины y₁, ... ,y₁₀₀ по следующей схеме:

а)  взять значения θ_i =10/i;

б)  воспользоваться формулами генерирования случайной величины с заданным законом распределения;

4.  Рассматривая значения y₁, ... ,y₁₀₀ как выборку из генеральной совокупности значений случайной величины Y, вычислить значения выборочных несмещенных оценок M[Y] и D[Y] для множества (y_i)  и . Рассчитать и построить оценку функции плотности вероятности f(y,θ);

5.  Используя метод максимального правдоподобия определить значения выборочных оценок параметров  для чего:

а)  сформировать функцию максимального правдоподобия;

б)  вывести уравнения правдоподобия для определения оценок параметров ;

в)  выписать в явном виде выражение для множественных оценок ;

г)  используя выборку y₁, ... ,y₁₀₀ определить значение выборочных оценок  для вектора (y_i)  и ;

6.  Для данного закона распределения привести соотношения, связывающие , M[Y] и D[Y];

7.  Используя эти соотношения и значения множественных оценок  определить оценки  и ;

8.  Сравнить результаты пунктов 4. и 7. и дать их интерпретацию.

Пункт 1. Обращения пользователей к серверу в случайные моменты времени являются потоком событий. Этот поток обладает свойствами:

¨  стационарности (вероятность появления k заявок пользователей за промежуток времени длительностью t зависит только от числа k и величины t)

¨  отсутствия последствия (вероятность появления k заявок пользователей за любой промежуток времени не зависит от предыстории потока)

¨  ординарности (вероятность появления более одной заявки за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одной заявки)

Таким образом, данный поток можно считать простейшим. Время между появлениями двух последовательных событий простейшего потока является непрерывной случайной величиной, распределенной по показательному закону.

Пункт 2. Показательным называют распределение вероятностей непрерывной случайной величины Y, которое описывается плотностью

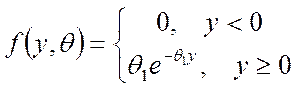
где θ₁ – постоянная положительная величина, характеризующая интенсивность потока.

Пункт 3. Показательное распределение определяется одним параметром. Согласно заданию его значение θ₁ = 10.

Формулами генерирования случайной величины с показательным законом распределения имеет вид:

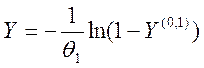
где Y^(0,1) – случайная величина с нормированным равномерным законом распределения.

Сгенерируем 100 значений случайной величины Y с показательным законом распределения:

Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10
0,239	0,038	0,052	0,096	0,171	0,049	0,091	0,051	0,104	0,094
Y11	Y12	Y13	Y14	Y15	Y16	Y17	Y18	Y19	Y20
0,016	0,011	0,074	0,210	0,001	0,053	0,028	0,156	0,314	0,162
Y21	Y22	Y23	Y24	Y25	Y26	Y27	Y28	Y29	Y30
0,062	0,114	0,089	0,021	0,171	0,197	0,136	0,030	0,021	0,079
Y31	Y32	Y33	Y34	Y35	Y36	Y37	Y38	Y39	Y40
0,169	0,016	0,098	0,081	0,179	0,218	0,034	0,030	0,116	0,030
Y41	Y42	Y43	Y44	Y45	Y46	Y47	Y48	Y49	Y50
0,206	0,193	0,062	0,068	0,153	0,061	0,031	0,051	0,119	0,010
Y51	Y52	Y53	Y54	Y55	Y56	Y57	Y58	Y59	Y60
0,050	0,058	0,099	0,006	0,047	0,037	0,026	0,134	0,103	0,060
Y61	Y62	Y63	Y64	Y65	Y66	Y67	Y68	Y69	Y70
0,046	0,044	0,049	0,025	0,163	0,141	0,043	0,544	0,245	0,113
Y71	Y72	Y73	Y74	Y75	Y76	Y77	Y78	Y79	Y80
0,015	0,004	0,038	0,095	0,148	0,040	0,054	0,129	0,002	0,026
Y81	Y82	Y83	Y84	Y85	Y86	Y87	Y88	Y89	Y90
0,100	0,242	0,048	0,019	0,038	0,070	0,010	0,030	0,025	0,103
Y91	Y92	Y93	Y94	Y95	Y96	Y97	Y98	Y99	Y100
0,013	0,325	0,061	0,222	0,061	0,128	0,168	0,006	0,143	0,160