Обоснование выбора закона распределения вероятностей, описывающего поведение случайной величины. Выписать аналитический вид кривой функции распределения вероятности соответствующего закона распределения, страница 2

Пункт 4. Вычислим значения выборочных несмещенных оценок M[Y] и D[Y] по формулам:

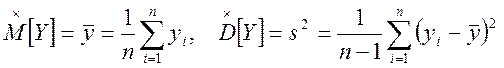
Получим следующие значения:

n
10	0,047	0,182
100	0,095	0,004

Построим оценку функции плотности вероятности в виде гистограммы. Для этого построим вариационный ряд:

Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10
0,001	0,002	0,004	0,006	0,006	0,010	0,010	0,011	0,013	0,015
Y11	Y12	Y13	Y14	Y15	Y16	Y17	Y18	Y19	Y20
0,016	0,016	00,019	0,021	0,021	0,025	0,025	0,026	0,026	0,028
Y21	Y22	Y23	Y24	Y25	Y26	Y27	Y28	Y29	Y30
0,030	0,030	0,030	0,030	0,031	0,034	0,037	0,038	0,038	0,038
Y31	Y32	Y33	Y34	Y35	Y36	Y37	Y38	Y39	Y40
0,040	0,043	0,044	0,046	0,047	0,048	0,049	0,049	0,050	0,051
Y41	Y42	Y43	Y44	Y45	Y46	Y47	Y48	Y49	Y50
0,051	0,052	0,053	0,054	0,058	0,060	0,061	0,061	0,061	0,062
Y51	Y52	Y53	Y54	Y55	Y56	Y57	Y58	Y59	Y60
0,062	0,068	0,070	0,074	0,079	0,081	0,089	0,091	0,094	0,095
Y61	Y62	Y63	Y64	Y65	Y66	Y67	Y68	Y69	Y70
0,096	0,098	0,099	0,100	0,103	0,103	0,104	0,113	0,114	0,116
Y71	Y72	Y73	Y74	Y75	Y76	Y77	Y78	Y79	Y80
0,119	0,128	0,129	0,134	0,136	0,141	0,143	0,148	0,153	0,156
Y81	Y82	Y83	Y84	Y85	Y86	Y87	Y88	Y89	Y90
0,160	0,162	0,163	0,168	0,169	0,171	0,171	0,179	0,193	0,197
Y91	Y92	Y93	Y94	Y95	Y96	Y97	Y98	Y99	Y100
0,206	0,210	0,218	0,222	0,239	0,242	0,245	0,314	0,325	0,544

Определим число интервалов k и их длину h:

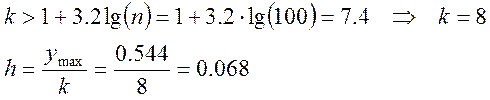
Определим относительные частоты попаданий в заданные интервалы:

x_i, x_i+1	n_i	W_i	W_i/h
[0.001, 0.069]	40	0.4	6,612
(0.069, 0.137]	27	0.27	4,463
(0.137, 0.205]	16	0.16	2.645
(0.205, 0.273]	6	0.06	0.992
(0.273, 0.341]	4	0.04	0.661
(0.341, 0.409]	2	0.02	0.331
(0.409, 0.477]	2	0.02	0.331
(0.477, 0.544]	3	0.03	0.496

По полученным данным построим гистограмму:

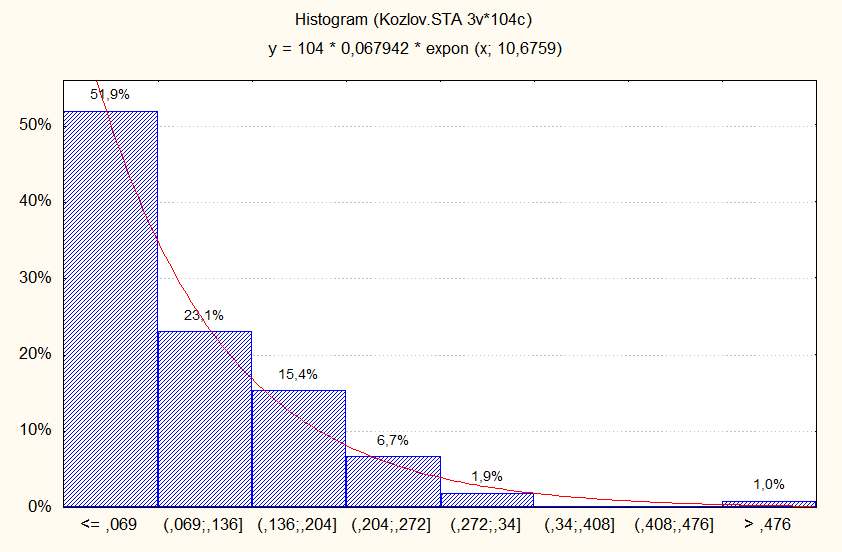
Пункт 5. Сформируем функцию максимального правдоподобия:

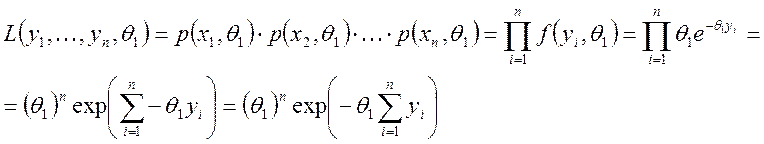
Логарифмическая функция правдоподобия будет иметь вид:

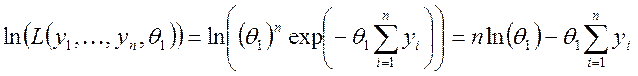
Выведем уравнение правдоподобия и найдем его корень:

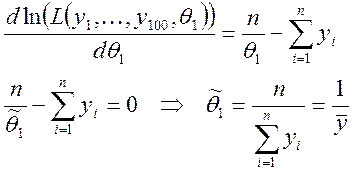
Определим значение выборочных оценок :

n
5	6.289
10	8.333

Пункт 6. Соотношения, связывающие , M[Y] и D[Y] имеют вид:

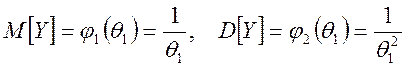
Пункт 7. Определим оценки и :

n
5	0.15	0.250
10	0.047	0.182

Пункт 8.

n
5	-	-	0.15	0.250
10	0,047	0,182	0.047	0.182
100	0,095	0,004	-	-

[Y] = c.

Оценки, полученные в пункте 7, являются наиболее эффективными (т.к. они получены с помощью метода максимального правдоподобия), однако имеют смещение относительно истинного значения. Оценки , полученные в пункте 4, так же являются эффективными, а про оценки , хотя они и имеют меньшее смещение, этого сказать нельзя.

1 2

Скачать файл