Отчёт по лабораторной работе №2
Тема:
«Оценивание функции плотности и интегрального закона распределения вероятностей по выборке заданного объема»
Выполнил: Козлов М.А.
Группа: А-01-03
Проверил:
Москва, 2005г.
Тема: Оценка функции плотности и интегрального закона распределения вероятностей по выборке заданного объема.
1. Создание и упорядочивание выборки объёмом в 10 значений.
№ XV_10: -2,463; -2,787; 4,093; 0,742; 1,431; -3,885; 1,816; 2,037; -0,797; -3,555;
Здесь первый столбец – номер значения по выборке (в упорядоченном по возрастанию виде), а второй – значение элемента выборки.
Гистограмма по значениям выборки:
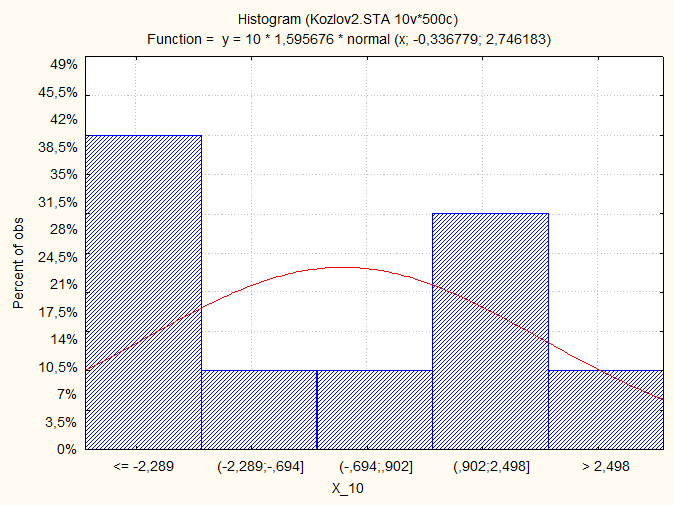
Диаграмма накопленных частот:
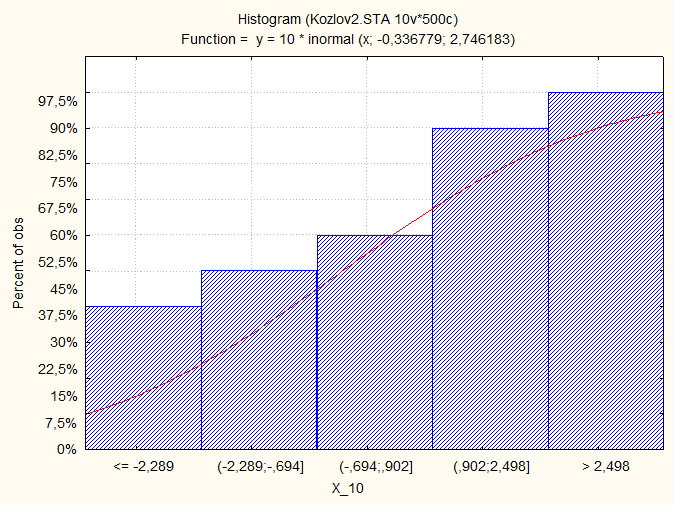
2. Создание выборки размером в 500 значений.
Гистограмма:
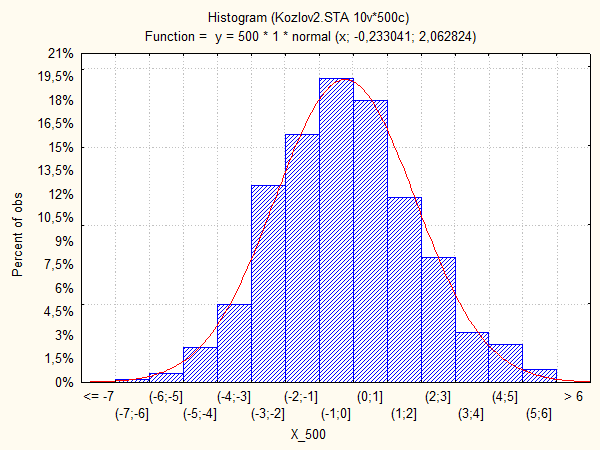
Диаграмма накопленных частот:
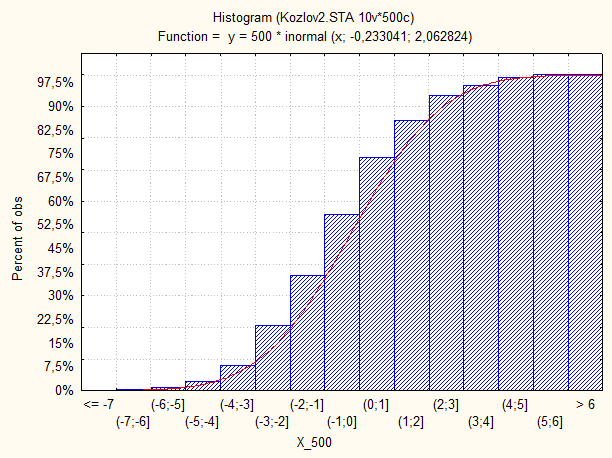
Вывод: при увеличении числа опытов гистограмма точнее повторяет форму подгоночной кривой (функции плотности и интегрального закона распределения вероятностей).
3. Создание новых случайных величин.
Гистограмма Y1 = Rnd(1):
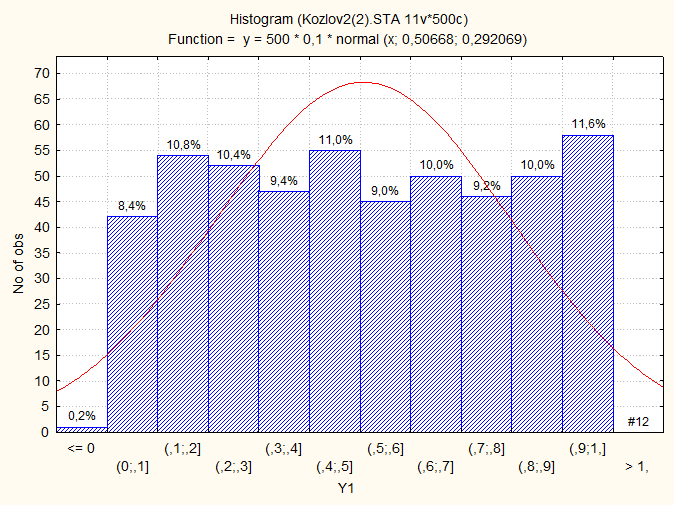
Гистограмма Z1 = Ln(Y1+1):
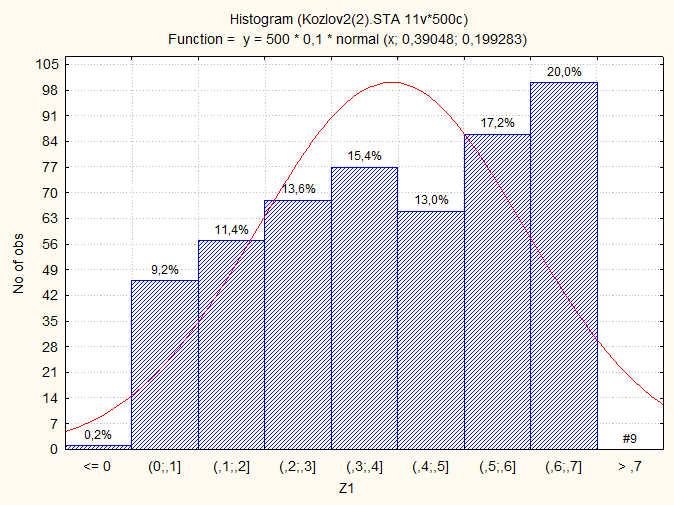
Гистограмма Z2 = 10*Y1:
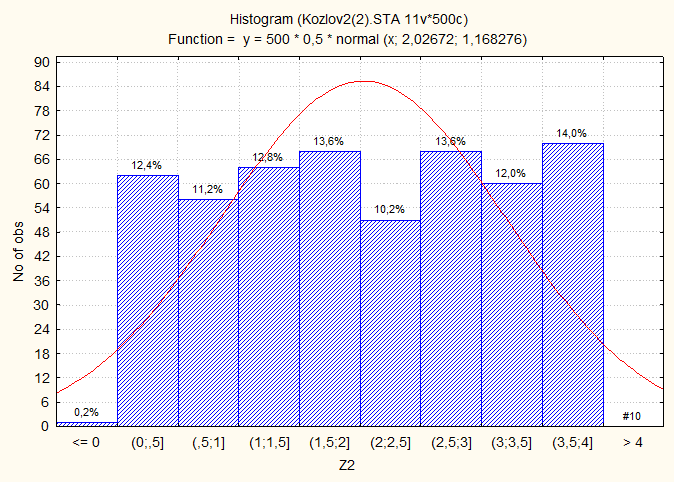
Гистограмма Z3 = Y1+10:
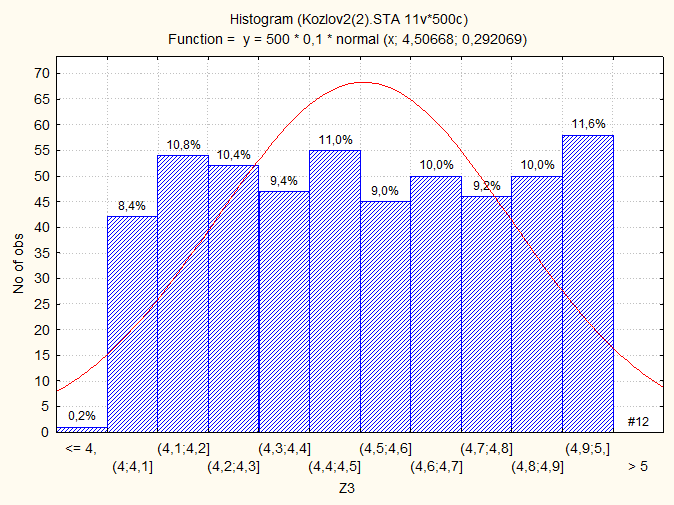
Гистограмма Z4 = (SYi-1)/Ö(1/6) , i=1, 2:
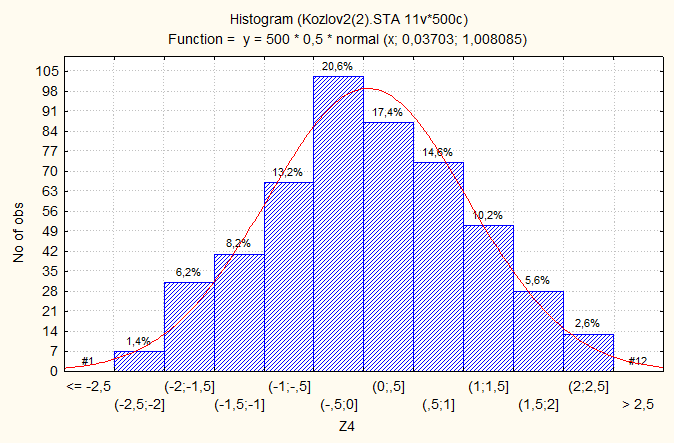
Гистограмма Z5 = (SYi-3)/Ö(1/2), i=1..6:
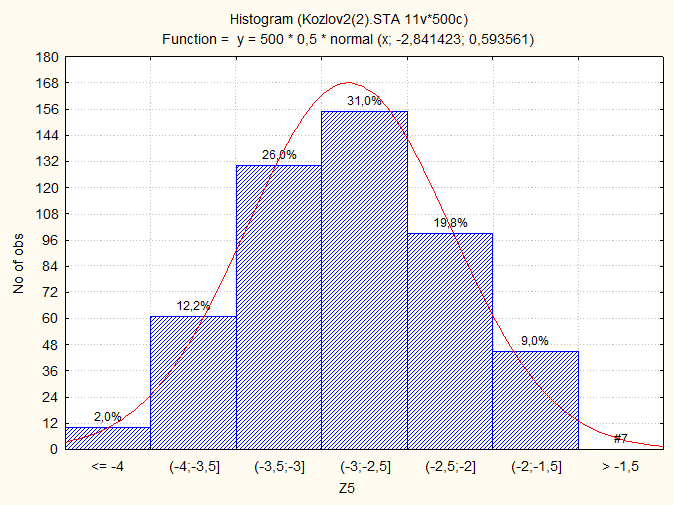
Вывод: Взятие логарифма уменьшает интервал распределения, а положение максимума смещается . При добавлении константы смещает интервал распределения на эту константу, а при умножении на константу – увеличивается на эту константу. При увеличении количества случайных величин, входящих в формулу для расчета значений столбца интервал распределения увеличивается, кривая вытягивается вдоль вертикальной оси, а гистограмма точнее повторяет форму подгоночной кривой.
4. Построение нового графика для первой выборки.
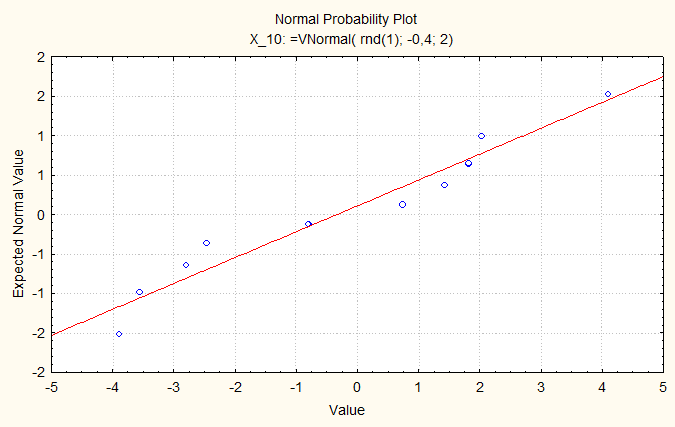
И для выборки в 500 значений:
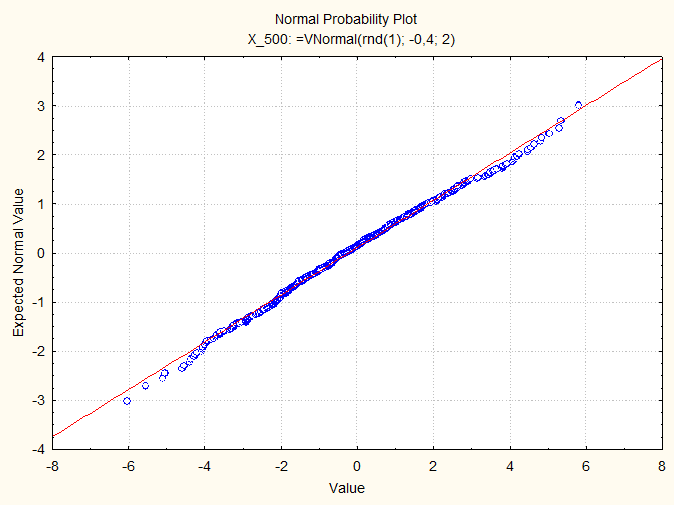
Вывод: Данный метод анализа позволяет линейно аппроксимировать график по зашумленным входным данным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.