Расчет случайной величины Y (суммарный объём электронной почты за сутки)

Московский Энергетический Институт

(Технический Университет)

Типовой расчёт по Статистике.

Вариант №2

Выполнил: Дербенёв Н. В.

Группа А-2-03

Москва 2005г

Постановка задачи.

В почтовый ящик электронной почты регулярно приходят сообщения разной длины в килобайтах. Суммарный объём почты за сутки - случайная величина Y.

1)         Величина Y представляет собой сумму случайных объёмов приходящих писем, что характерно для процесса роста. Следовательно, распределение случайной величины Y соответствует логнормальному закону распределения.

2)         Аналитический вид кривой f(y,q)~LN(q) имеет вид:

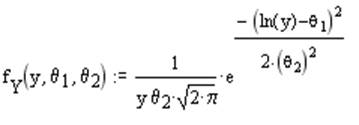
3)         Зададим параметры распределения (q = êq1, q2ú ) по следующему правилу:

            q1=№/10, q2=№/20

   Где № - номер по журналу (№ = 2). Учитывая это, получаем:

q1=0.2, q2=0.1

4)         С помощью пакета Statistica рассчитаем 100 значений случайной величины (Y~ LN(q)) с параметрами q1, q2.

1	1.498	26	1.408	51	1.233	76	1.030
2	1.227	27	1.293	52	1.241	77	1.221
3	1.175	28	1.241	53	1.246	78	1.147
4	1.114	29	1.487	54	1.411	79	1.163
5	1.132	30	1.218	55	1.100	80	1.211
6	1.225	31	1.183	56	1.345	81	1.258
7	1.328	32	1.358	57	1.346	82	1.167
8	1.291	33	1.130	58	1.341	83	1.126
9	1.220	34	1.242	59	1.354	84	1.232
10	1.255	35	1.114	60	1.178	85	1.061
11	1.166	36	1.497	61	1.384	86	1.563
12	1.109	37	1.175	62	1.095	87	1.307
13	1.286	38	1.187	63	1.140	88	1.037
14	1.158	39	1.426	64	1.316	89	1.296
15	1.151	40	1.206	65	1.016	90	1.257
16	1.208	41	1.204	66	0.962	91	1.389
17	1.287	42	1.173	67	1.212	92	1.273
18	1.305	43	1.091	68	1.212	93	1.228
19	1.193	44	1.192	69	1.117	94	1.557
20	1.105	45	1.391	70	1.320	95	1.213
21	1.319	46	1.144	71	1.244	96	1.271
22	1.232	47	1.282	72	1.239	97	1.342
23	1.120	48	1.168	73	1.297	98	1.374
24	1.268	49	1.421	74	1.311	99	1.178
25	1.407	50	1.062	75	1.353	100	1.215

Значения были сгенерированы, использую следующие операции:

а)U1..Un, Ui~N(0,1)

б)Y1..Yn,  , Yi~LN(q1,q2)
5)         Запишем формулы для нахождения несмещённых оценок M[Y] и D[Y]:

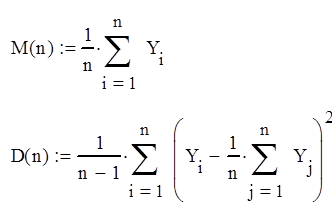
По этим формулам с помощью пакета Mathcad находим наши оценки:

	n=10	n=100
M[Y]	1.2465	1.24201
D[Y]	0.0121411667	0.0137

6)         С помощью пакета Statistica строим оценку функции плотности вероятности в виде гистограммы по значениям Yi, i=1..100.

Кол-во интервалов

n=8

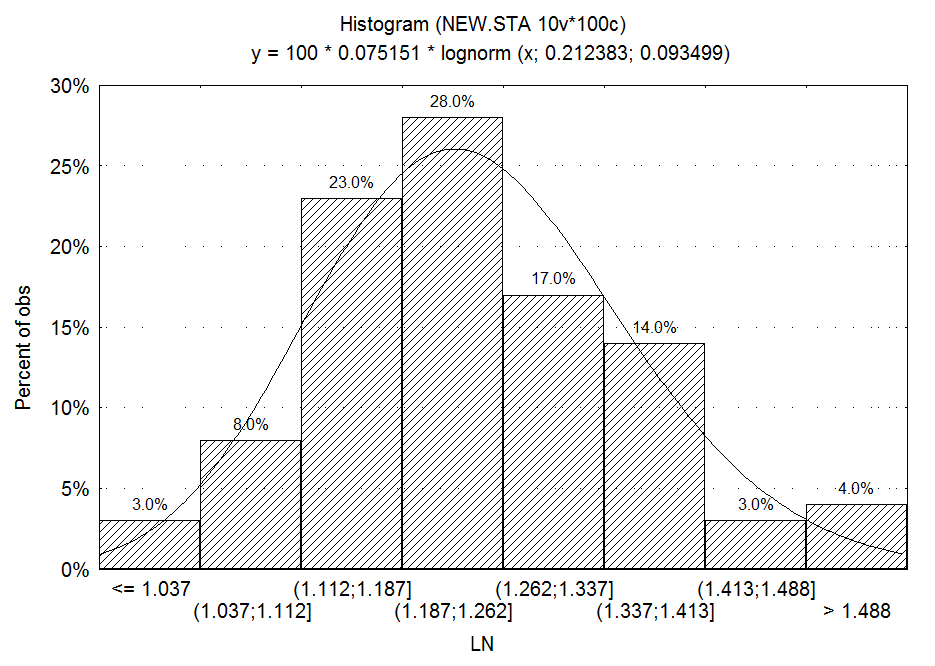
7)         Используя метод максимального правдоподобия, рассчитаем оценки параметров

(q = êq1, q2ú ) логарифмического закона распределения.

а) Функция максимального правдоподобия имеет вид:

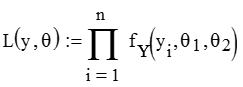
Конкретно для логнормального закона распределения:

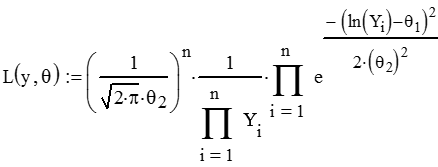
            Для удобства возьмём натуральный логарифм от функции максимального правдоподобия:

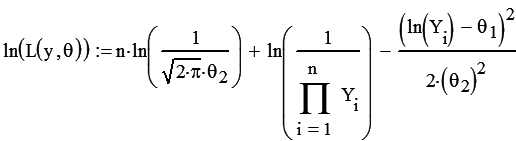
б) Выведем уравнения правдоподобия для нахождения q1 и q2.

Для этого нужно найти: при каких q1 и q2 функция максимального правдоподобия ln(L(y,q)) достигает своего максимума, следовательно, производные этой функции по q1 и q2 равны нулю. Из этих соотношений находим наши параметры распределения:

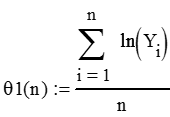
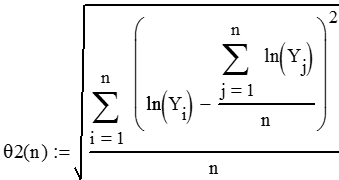
в) По этим формулам с помощью пакета Mathcad находим наши параметры распределения:

	n=10	n=100
q1	0.21699	0.21239
q2	0.08085	0.09303

8)         Для логнормального закона распределения запишем соотношения, связывающие математическое ожидание и дисперсию с параметрами q1и q2

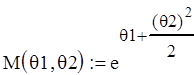
9)         По формулам пункта 8 (где q1 и q2 берётся из пункта 7) с помощью пакета Mathcad находим наши оценки:

	n=10	n=100
M[q1,q2]	1.2464	1.24199
D[q1,q2]	0.01019	0.01341

10)       Значения оценок математического ожидания в пунктах 5 и 9 практически одинаковы. Эти оценки несмещённые и состоятельные.

Значение оценок дисперсии в пунктах 5 и 9 не равны. Они обе состоятельные, но оценка, посчитанная в пункте 9, имеет значительное смещение при выборке малого объёма. При увеличении объёма выборки смещение уменьшается. Из этого следует, что эта оценка асимптотически несмещённая.

Оценки, рассчитанные по формулам пункта 5 асимптотически эффективны. Эффективность оценок рассчитанных по методу максимального правдоподобия больше, поэтому эти оценки эффективны.