Выполнили |
бригада №8 |
Студенты: |
Архипов А. Е. |
|
Попов И. О. |
|
|
Группа |
А – 01 – 03 |
|
Дата |
23.03.06 |
Принял |
|
Преподаватель |
|
Дата |
Введение
Цель работы - закрепление теоретического материала по исследованию динамических систем второго порядка методом фазовой плоскости.
В первой части работы проводится исследование линейных САУ методом фазовой плоскости. В этой части строится фазовый портрет для двух случаев линейных систем: имеющих особую точку фазового портрета – эллипс и неустойчивый узел.
Во второй части проводится исследование динамики нелинейных САУ. Сначала проводится исследование динамических свойств каждого из линейных описаний НСАУ. Затем методом фазовой плоскости исследуются динамические свойства заданной НСАУ. И наконец, исследуется влияние изменения параметров системы и нелинейного элемента на свойства системы в целом.
Постановка задачи
Типы особой точки фазового портрета исследуемой линейной системы 2-го порядка:
а) неустойчивый узел;
б) устойчивый фокус.
Структурная схема исследуемой НСАР имеет вид:
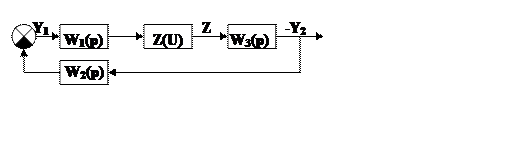
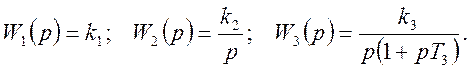
Характеристика нелинейного элемента имеет вид:
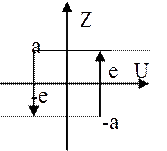
(Двухпозиционное реле с гистерезисом)
Значения параметров:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
1. Исследование динамики линейных САУ методом фазовой плоскости.
Уравнения движения линейной САУ второго порядка имеют вид:
![]()
или в форме переменных состояния:
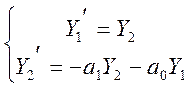
Исследуем динамику системы при наличии особой точки фазового портрета следующих типов:
а) неустойчивый узел:
Должны выполняться условия ![]() ,
, ![]() ,
, ![]() . Имеет место расходящийся
апериодический процесс. Выберем
. Имеет место расходящийся
апериодический процесс. Выберем ![]() ,
, ![]() .
.
Фазовый портрет системы имеет вид:
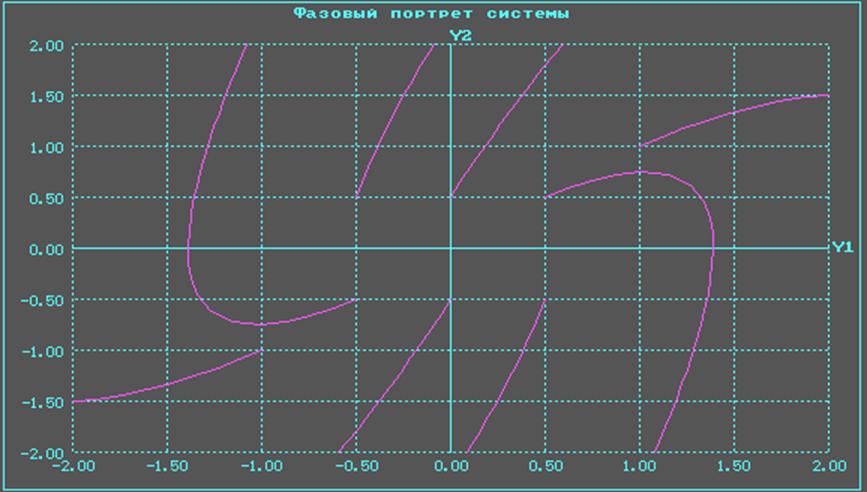
Анализ переходных процессов в системе:
|
|
|
|
|
|
|
|
б) устойчивый фокус:
Должны выполняться условия ![]() ,
, ![]() ,
, ![]() . Фазовые
траектории имеют вид спиралей. Начало координат является точкой устойчивого
равновесия. Выберем
. Фазовые
траектории имеют вид спиралей. Начало координат является точкой устойчивого
равновесия. Выберем ![]() ,
, ![]() .
.
Фазовый портрет системы имеет вид:
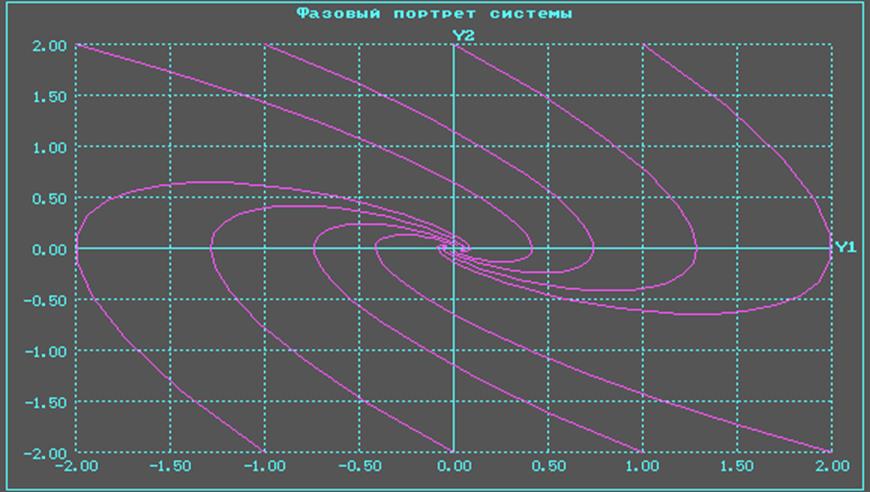
Анализ переходных процессов в системе:
|
|
|
|
|
|
|
|
2. Исследование динамики нелинейных САУ.
Запишем в форме переменных состояния уравнения движения исследуемой НСАУ:
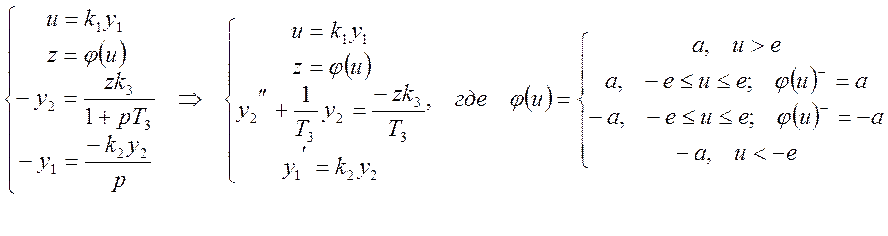
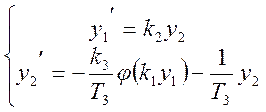
Т. о. будут наблюдаться 2 типа уравнений движения:
|
тип 1: |
тип 2: |
|
|
|
Проведем анализ вида фазовых траекторий, соответствующих описанию системы, полученному для каждого из линейных участков на характеристике нелинейного звена:
а) тип 1:
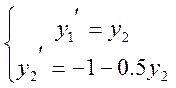
Фазовые траектории имеют вид:
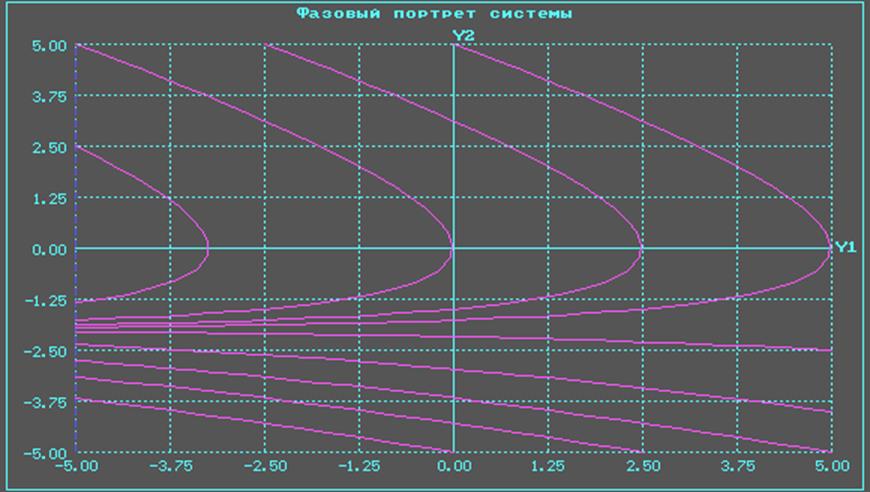
Анализ переходных процессов в системе:
|
|
|
|
|
|
|
|
б) тип 2:
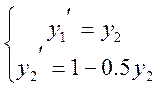
Фазовые траектории имеют вид:
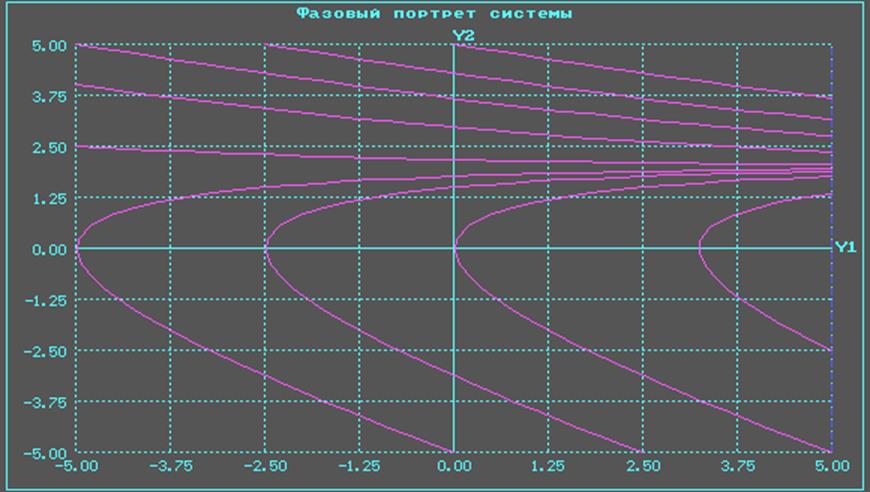
Анализ переходных процессов в системе:
|
|
|
|
|
|
|
|
Полупрямые переключения будут описываться уравнениями вида:
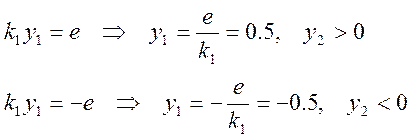
Исследование методом фазовой плоскости динамических свойств НСАУ:
Фазовый портрет системы имеет вид:
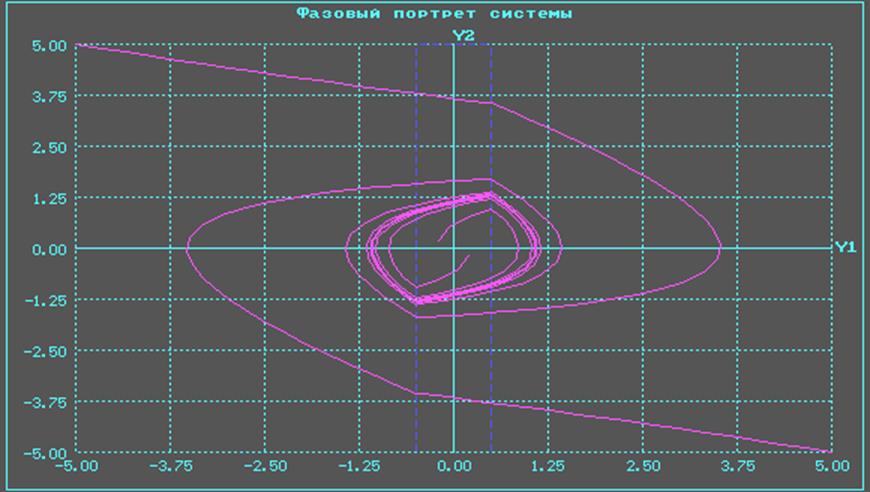
Анализ переходных процессов в системе:
|
|
|
|
|
|
|
|
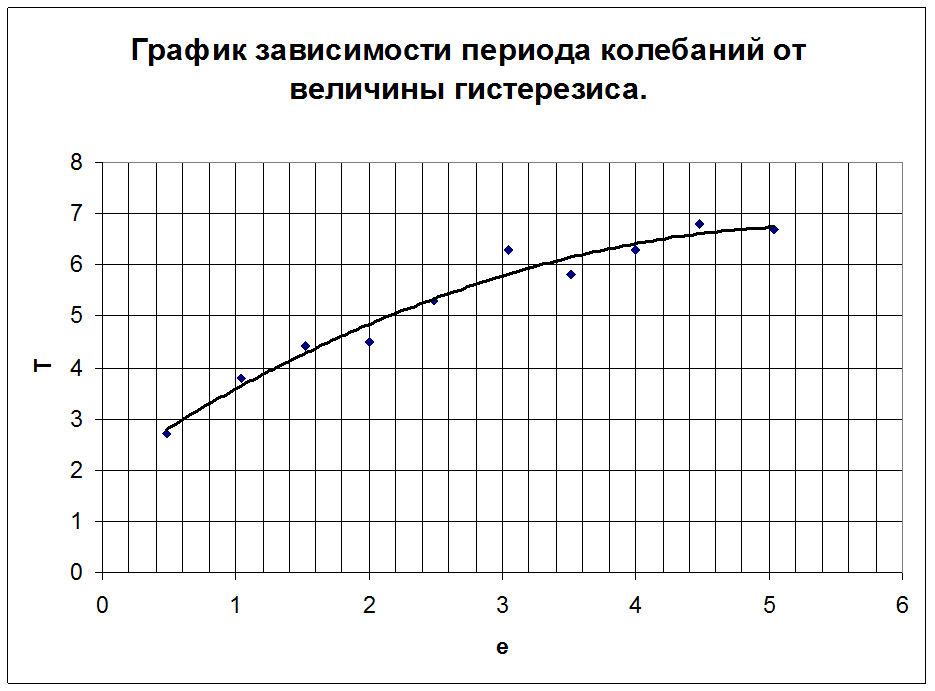
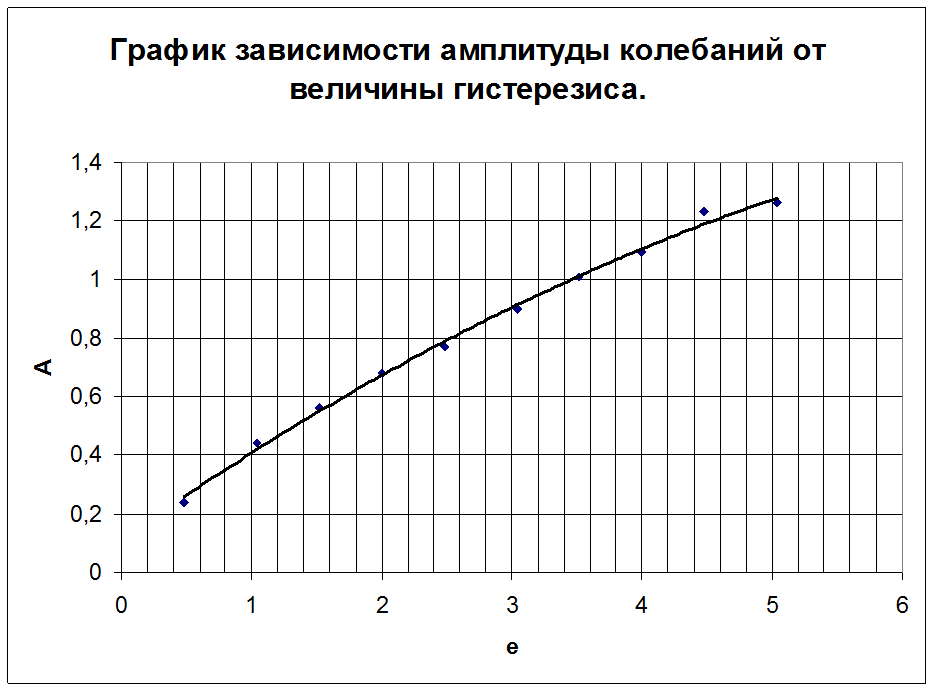
Исследование зависимости параметров (периода и амплитуды колебаний) устойчивого предельного цикла, имеющего место в системе при изменении величины гистерезиса переключающего звена в диапазоне [0, 5]:
|
величина гистерезиса, e |
период колебаний, T |
амплитуда колебаний, A |
|
0 |
- |
- |
|
0,48 |
2,7 |
0,24 |
|
1,04 |
3,8 |
0,44 |
|
1,52 |
4,4 |
0,56 |
|
2 |
4,5 |
0,68 |
|
2,48 |
5,3 |
0,77 |
|
3,04 |
6,3 |
0,9 |
|
3,52 |
5,8 |
1,01 |
|
4 |
6,3 |
1,09 |
|
4,48 |
6,8 |
1,23 |
|
5,04 |
6,7 |
1,26 |
Построение графиков по результатам исследования:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.