Сумматоры. Изучение работы полусумматора, и его таблицы истинности. Изучение работы полного сумматора

Лабораторная работа 2.1

Сумматоры

Основные теоретические положения

Сумматором называется комбинационное логическое устройство, предназначенное для выполнения операции арифметического сложения чисел, представленных в виде двоичных кодов. Операция вычитания заменяется сложением чисел в обратном или дополнительном кодах. Операции умножения и деления сводятся к реализации многократных сложений и сдвигов.

Сумматор складывает числа поразрядно, учитывая перенос из младшего разряда и формируя результат сложения и перенос в старший разряд. По числу входов различают: полусумматоры, полные сумматоры. Файлы для моделирования этих элементов расположены в папке Lab_2_1\Модели, в них используются индикаторы, которые отражают происходящие операции с логическими функциями. В описании иногда приведены рисунки без части индикаторов, имеющихся в моделях, для экономии места.

1 Полусумматор

Полусумматор (HS) складывает два двоичных числа одного, самого младшего разряда A₀, B₀ без учета переноса в этот разряд (младше разрядов нет). Выходные значения: результат сложения S₀ и перенос в старший разряд P₀ представлены в таблице истинности (табл. 1).

Таблица истинности полусумматора          Таблица 1

A0	B0	S0	P0
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Из таблицы 1 следуют аналитические выражения выходных сигналов:

 

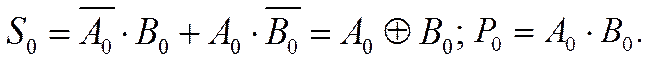(1)

Для арифметического сложения в одном разряде двоичной системы счисления используется логическая операция «Исключающее ИЛИ», для получения переноса – логическая операция «Умножение».

Задание 1. С помощью комбинаций входных логических сигналов, изучить работу полусумматора, и его таблицу истинности.

Полусумматор Half Adder (файл L2_add_01.ewb) и его таблица истинности представлена на рисунках 1, 2, где используются следующие обозначения:

- A₀, B₀ – слагаемые двоичные числа разряда 0;

- Sum₀ – результат сложения в разряде 0;

- carry 0 (carry out)– перенос результата сложения из разряда 0 в старший разряд 1.

Перенос возможен в том случае, если A₁A₀ + B₁B₀ = 01+01=10, где carry out =1, Sum₀ =0.

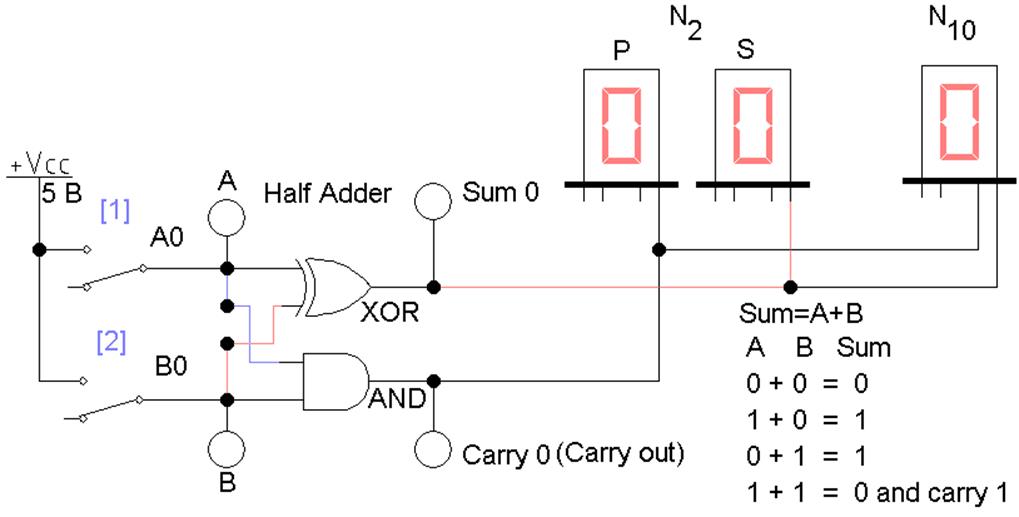
Рис. 1 Схема полусумматора на логических элементах

L2_add_02.ewb – полусумматор из поля компонентов Digital и его таблица истинности (рис. 2).

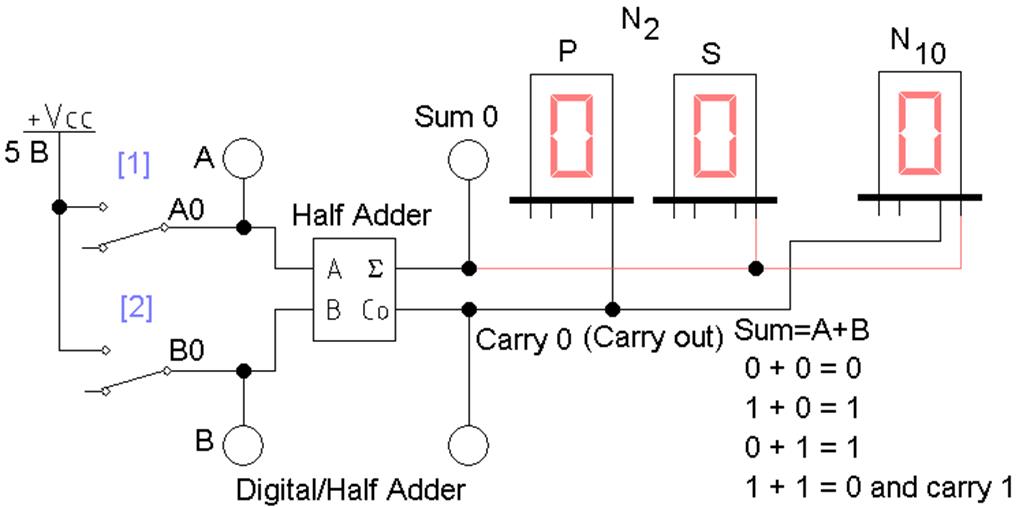
Рис. 2 Схема полусумматора

2 Полный сумматор

Одноразрядный полный сумматор (рис. 3) складывает три двоичных числа и имеет соответствующие им входы: для разряда слагаемого A_n, разряда слагаемого B_n, входного сигнала переноса из младшего разряда carry in.

Результат сложения: Sum _n и перенос в старший разряд carry out.

Полный сумматор состоит из трех полусумматоров (рис. 3).

Следовательно, суммирование осуществляется аналогично сложению «в столбик».

Задание 2

С помощью комбинаций входных логических сигналов изучить работу полного сумматора (файлы L2_add_03.ewb- L2_add_03.ewb_07), и его таблицу истинности.

Полный сумматор Full Adder (файл L2_add_03.ewb) и его таблица истинности (рис. 3, 4). Полусумматор для получения переноса можно заменить элементом ИЛИ.

На первом полусумматоре складываются переменные, на втором к результату добавляется перенос из младшего разряда, третий используется для расчета переноса.

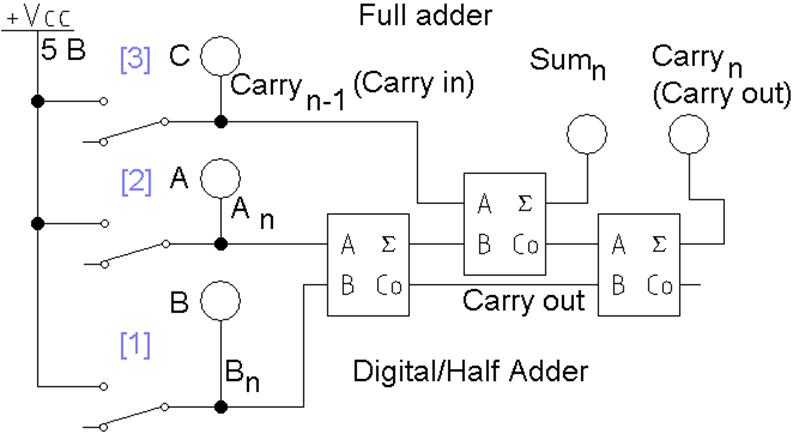
Рис. 3 Схема одноразрядного полного сумматора на полусумматорах (без части индикаторов)

L2_add_04.ewb – полный сумматор из поля компонентов Digital и его таблица истинности (рис. 4).

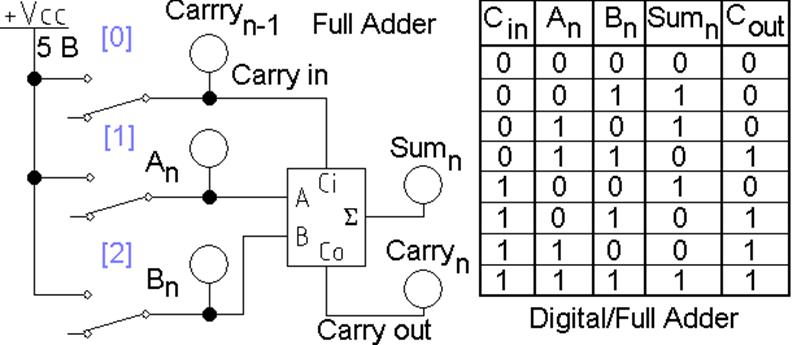
Рис. 4 Схема одноразрядного полного сумматора (без части индикаторов) и таблица истинности

Модель в файле L2_add_05.ewb – полный двухразрядный сумматор сложения двоичных чисел A₁, A₀ и B₁, B₀ и его таблица истинности (рис. 5).

Обозначения на рисунках:

A₁A₀, B₁B₀ – слагаемые двухразрядные двоичные числа разрядов 1 и 0;

- Sum₀ – результат сложения в младшем разряде 0;

- Sum₁ – результат сложения в старшем разряде 1;

- carry 0 – перенос внутри сумматора из разряда 0, как результат сложения A₀ и B₀,  в старший разряд 1, на выходе сумматора его нет;

- carry out – перенос из разряда 1 в следующий старший разряд 2.

В данном примере не учитывается перенос из разряда, младше 0, считается, что его нет. Поэтому при суммировании в разряде 0 использован полусумматор. В файле приводится пример сложения Example.

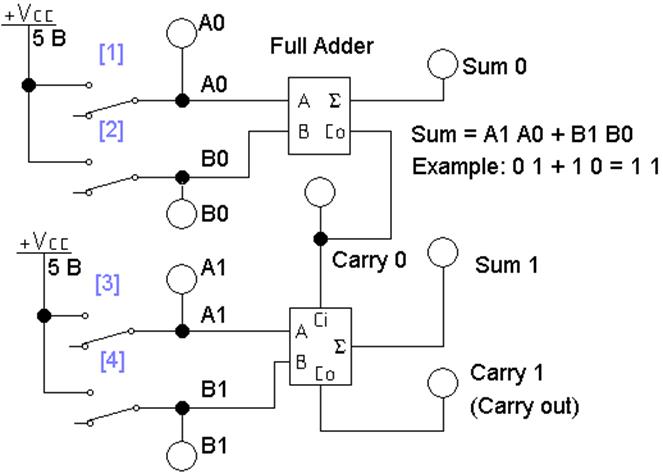
Рис. 5 Схема полного двухразрядного сумматора (без части индикаторов)

3 Вычитатели

Операция вычитания осуществляется путем изменения знака вычитаемого и сложения с уменьшаемой величиной. Изменение знака осуществляется переводом вычитаемого в дополнительный код.

Для распознавания знака числа используется старший разряд (знаковый разряд). У положительных чисел он равен нулю, у отрицательных чисел равен единице.

При выполнении операций сложения и вычитания возможны ошибки, если количество разрядов результата вычислений превышает разрядность вычислительных устройств.

Например, результат сложения чисел на калькуляторе превышает его возможности отображения, при этом старший разряд может быть утрачен.

Пример: вычислить: 4 +(– 3), результат представить в четырехразрядном двоичном коде. Пятый разряд использовать как знаковый. Ответ в табл. 2.

Последовательность операции вычитания                                                  Таблица 2

Двоичное число		Десятичное число		Комментарий
знак	модуль	знак	модуль
0	0100	+	4	Первое слагаемое (4 разряда)
0	0011	+	3	Вычитаемое в полном формате (4 разряда)
1	1100	–		Поразрядная инверсия вычитаемого
0	0001	+	1	Добавление единицы младшего разряда
1	1101	–	3	Второе слагаемое в дополнительном коде
0	0001	+	1	Результат вычитания

Если при добавлении дополнения в n – разрядном представлении есть перенос в n +1 разряд (второе слагаемое в дополнительном коде табл. 2), то результат является положительным числом.

3.1 Одноразрядный полувычитатель

Данное устройство определяет разницу двух одноразрядных двоичных чисел без учета займа в младший разряд. Результат вычитания D₀ и займ из старшего разряда E₀ представлены в таблице истинности (табл. 3).