3.5 Сумматоры
Комбинационный сумматор – это цифровое устройство, предназначенное для арифметического сложения чисел, представленных в виде двоичных кодов.
Обычно сумматор представляет собой комбинацию одноразрядных сумматоров. При сложении двух чисел в каждом разряде производится сложение трех цифр: цифры первого слагаемого Ai, цифры второго слагаемого Bi и цифры переноса из младшего разряда Pi-1. В результате суммирования на выходных шинах получается сумма S i и перенос в старший разряд P i.
Сумматоры с поразрядным переносом выпускаются в виде микросхем на 2 и 4 разряда. Например, К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8 необходимо взять две микросхемы и соединить их последовательно по цепи переноса.
Сумматор с поразрядным последовательным переносом наиболее прост с точки зрения схемной реализации, однако имеет низкое быстродействие. Время выполнения операции зависит от разрядности так как включает в себя затраты времени на вычисление во всех более младших разрядах и выполнение в них переносов.
Для повышения быстродействия используются сумматоры с параллельным переносом.
По числу входов различают: полусумматоры, полные сумматоры.
Полусумматор
Полусумматор (Half Summator) складывает два числа самого младшего разряда A, B без учета переноса. Результат сложения S и перенос в старший разряд P (рис.1) значения, которых представлены в таблице истинности (табл.1).
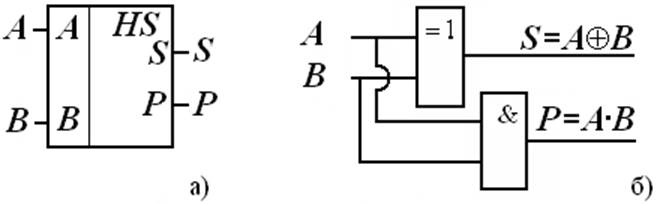
Рис. 1 Обозначение одноразрядного полусумматора, (а),
и его функциональная схема, (б).
Таблица истинности полусумматора Таблица 1
|
Набор |
Первое слагаемое |
Второе слагаемое |
Результат |
|
|
Сумма |
Перенос |
|||
|
A |
B |
S |
P |
|
|
1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
1 |
0 |
|
3 |
1 |
0 |
1 |
0 |
|
4 |
1 |
1 |
0 |
1 |
Из таблицы 1 следует, что, если A = 1 и B = 1, то происходит переполнение разряда S = 0 и вырабатывается сигнал переноса в старший разряд P = 1.
Вывод: максимальное значение результата сложения на полусумматоре с учетом переноса равно: A0 + B0 = 12+12 = 102 = 210, где P0 = 1, S0 = 0.
Аналитические выражения выходных сигналов:
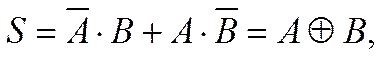 |
|||
Полный сумматор
Одноразрядный полный сумматор (Summator) имеет три входа: для разряда слагаемого An, разряда слагаемого Bn и входного сигнала переноса из младшего разряда Pn-1.
Результат сложения Sn и перенос в старший разряд Pn (рис. 3.2) значения, которых представлены в таблице истинности (табл. 2).
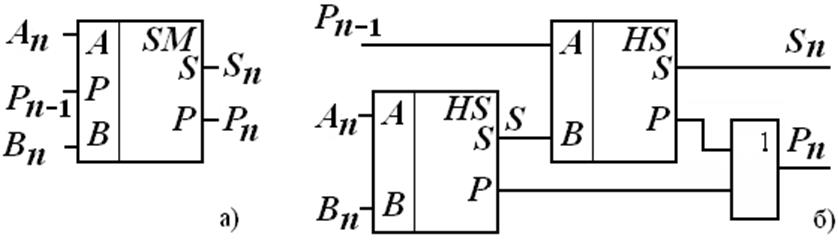
Рис. 2 Обозначение одноразрядного полного сумматора, (а),
и его функциональная схема на полусумматорах, (б).
Вместо элемента 2ИЛИ можно использовать третий полусумматор, у которого S = P n.
Таблица истинности одноразрядного полного сумматора Таблица 2
|
Набор |
Первое слагаемое |
Второе слагаемое |
Перенос |
Результат |
|
|
Сумма |
Перенос |
||||
|
An |
B n |
P n –1 |
S n |
P n |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
1 |
1 |
0 |
|
3 |
0 |
1 |
0 |
1 |
0 |
|
4 |
0 |
1 |
1 |
0 |
1 |
|
5 |
1 |
0 |
0 |
1 |
0 |
|
6 |
1 |
0 |
1 |
0 |
1 |
|
7 |
1 |
1 |
0 |
0 |
1 |
|
8 |
1 |
1 |
1 |
1 |
1 |
Вывод: сложение в двоичной системе производится с учетом переноса из младшего разряда аналогично «сложению в столбик» в десятичной системе. При этом максимальное значение результата сложения в одном разряде с учетом переносов равно: An + Bn + Pn-1 = 12+12+12 = 112 = 310, где Pn = 1, Sn = 1.
Как видно из карт Карно, функция результата не минимизируется, а функция переноса упрощается (табл. 3), что сделано также в аналитическом виде и реализовано на логических элементах (рис. 3).
Из таблицы истинности следуют выражения для сигналов:
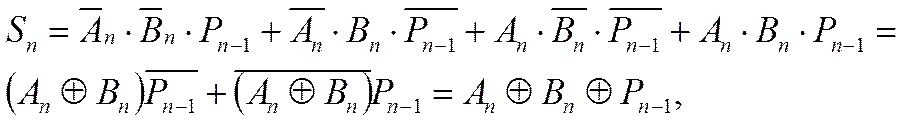 |
|||
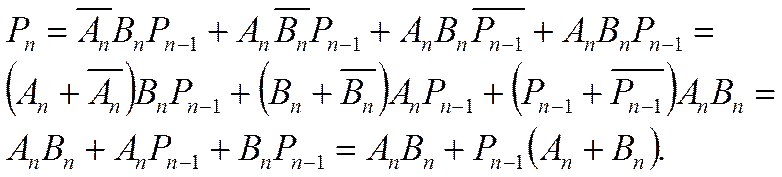 |
|||
(1)
Карта Карно для Sn Карта Карно для Pn Таблица 3
|
An Bn Pn-1 |
00 |
01 |
11 |
10 |
An Bn Pn-1 |
00 |
01 |
11 |
10 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
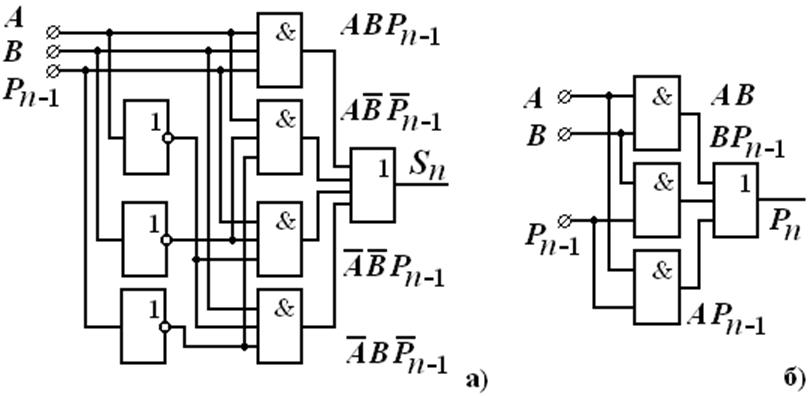
Рис. 3 Принципиальная схема одноразрядного полного сумматора
на элементах И, ИЛИ, НЕ: получение суммы (а), и переноса, (б).
Параллельный многоразрядный сумматор состоит из n одноразрядных сумматоров (рис. 4). Входные сигналы подаются на одноразрядные сумматоры одновременно. Если появляются сигналы переноса, то они поступают в старший разряд.
Вывод: пока не состоится сложение в младшем разряде и не определится значение переноса не может быть определена сумма в разряде более старшем.
Максимальное значение результата сложения с учетом переносов: Pn, Sn = 112 = 310.
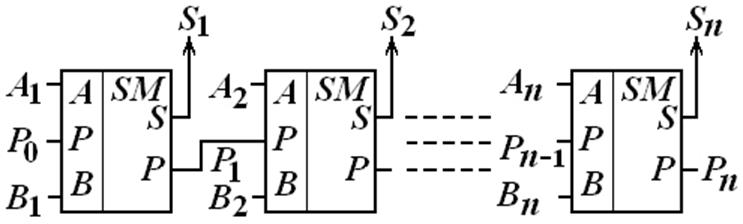
Рис. 4 Параллельный многоразрядный сумматор
При использовании обратного кода перенос из самого старшего разряда подается на вход переноса самого младшего разряда. В остальных случаях на вход самого младшего разряда подается логический ноль.
Сумматоры с поразрядным переносом выпускаются в виде микросхем на 2 и 4 разряда. Например, К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8 необходимо взять две микросхемы и соединить их последовательно по цепи переноса.
Сумматор с поразрядным последовательным переносом наиболее прост с точки зрения схемной реализации.
Быстродействие данного сумматора ограничено временем, за которое сигнал переноса последовательно распространяется через все разряды сумматора.
Этот недостаток отсутствует у параллельных сумматоров с параллельным переносом.
Параллельный сумматор с параллельным переносом
В данных устройствах сигнал переноса формируется с одновременным (параллельным) учетом всех переносов в младших разрядах, по отношению к рассматриваемому разряду.
Для построения сумматора с параллельным переносом используются две вспомогательные функции.
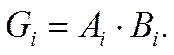 Функция генерации (порождения
переноса) – принимает единичное значение, если перенос на выходе данного
разряда появляется независимо от наличия или отсутствия входного переноса:
Функция генерации (порождения
переноса) – принимает единичное значение, если перенос на выходе данного
разряда появляется независимо от наличия или отсутствия входного переноса:
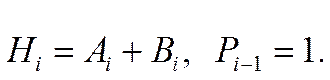 Функция прозрачности (транзита
переноса) – принимает единичное значение, если перенос на выходе данного
разряда появляется только при наличии входного переноса. Это следует из
выражения (3.1):
Функция прозрачности (транзита
переноса) – принимает единичное значение, если перенос на выходе данного
разряда появляется только при наличии входного переноса. Это следует из
выражения (3.1):
Тогда перенос на выходе младшего разряда:
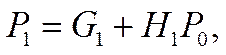 |
(2)
что, с учетом выражений для дополнительных функций, соответствует зависимости для определения переноса одноразрядного сумматора (1).
На выходе следующего разряда, согласно (1, 2):
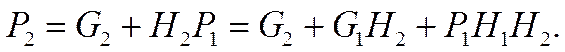 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.