Сумматоры. Полусумматоры и полные сумматоры. Параллельный сумматор с параллельным переносом. Сумматор-вычитатель, страница 3

Двоичное число		Десятичное число		Комментарий
знак	модуль	знак	модуль
0	0100	+	4	Первое слагаемое
0	0111	+	7	Вычитаемое в полном формате
1	1000	–		Инверсия вычитаемого
0	0001	+	1	Единица младшего разряда
1	1001	–	7	Сумма инверсии и 1 младшего разряда
1	1001	–	7	Второе слагаемое в дополнительном коде
1	1101	+		Сумма, переноса нет – число отрицательное
1	1101	–	3	Результат вычитания
0	0010	+		Инверсия результата
0	0001	+	1	Единица младшего разряда
0	0011	+	3	Сумма инверсии и 1 младшего разряда
0	0011	+	3	Модуль результата вычитания

Пример: представить значения + 0 и – 0 в двоичном коде. Ответ в табл. 7.

Последовательность операции вычитания              Таблица 7

Двоичное число	Десятичное число	Комментарий
0000	+ 0
1111		Инверсия кода 00002 = 010
0001	1	Единица младшего разряда
1  0000		1 отбрасывается
0000	– 0	Результат

При выполнении операций сложения и вычитания возможны ошибки, если количество разрядов результата вычислений превышает разрядность вычислительных устройств. Например, сложение двух больших положительных или больших отрицательных чисел.

Признаком ошибки, в данном случае, является не совпадение знаков переменных со знаком результата вычислений. Этот факт контролируется специальным устройством.

Ограничения представления чисел: без указания знака от 0 до 2ⁿ –1, где n – число разрядов. Восемь разрядов двоичного числа соответствует 0…255₁₀. Шестнадцать разрядов: от 0 до 65535₁₀ или 0 – FFFF₁₆.

Числа со знаком ограничены диапазоном: от – 2^n-1 до +2^n-1 –1, где n – число разрядов. Восемь разрядов двоичного числа соответствуют: от –128₁₀ до +127₁₀. Шестнадцать разрядов: от –32768 до +32767₁₀ или 8000…7FFF₁₆.

Сумматор – вычитатель

Схема устройства представлена на рис 6, а команды управления K₀ …K₄ в табл. 8. На вход сумматора – вычитателя подаются в параллельном коде два разряда переменной A (A₂A₁) и два разряда переменной B (B₂B₁).

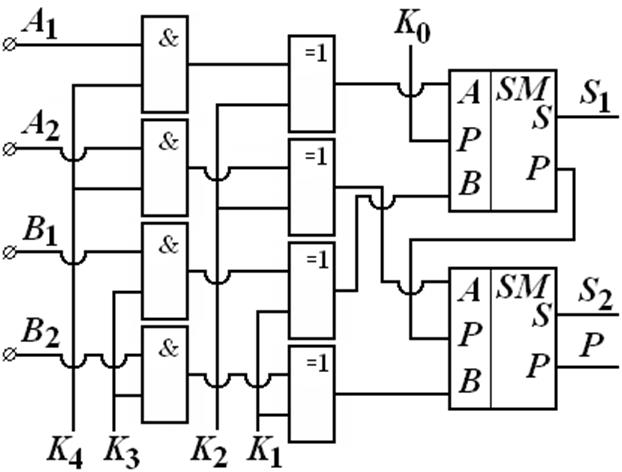
Рис. 6 Схема двухразрядного сумматора – вычитателя

Выходные сигналы: результат расчетов младшего разряда S₁, результат расчетов  старшего разряда S₂, P перенос – займ в следующий сумматор, это не знаковый разряд.

Элементы И формируют запрет поступления переменной А (команда К₄=0), а так же переменной В (команда К₃=0) в сумматор – вычитатель. При К₄=1, К₃=1 запрет отсутствует.

Элементы Исключающее ИЛИ позволяют инвертировать переменные А (К₂=1), В (К₁=1). Если К₂=0, К₁=0, то указанные элементы не изменяют входной сигнал.

Для получения отрицательного двоичного числа, например, при вычитании производят инверсию переменной и добавляют единицу в младший разряд (К₀=1) по методу вычитания в дополнительном коде.

Вывод:

- Вычитание в двоичной системе производится с учетом займа в младший разряд аналогично «вычитанию в столбик» в десятичной системе.

Максимальное значение результата вычитания в одном разряде с учетом займа равно: A_n – B_n – E_n-1 = 0₂ –1₂ –1₂ = 10₂ = –2₁₀, где E_n = 1, D_n = 0 (E_n вычитается, иначе говоря, заимствуется из старшего разряда).

- Перенос при сложении в дополнительном коде служит той же цели, что и займ в обычном вычитании. Отсутствие переноса в старшем разряде свидетельствует о том, что должен быть займ (это инверсные величины) и вычитаемое больше уменьшаемого.

- Пока не состоится вычитание в младшем разряде и не определится значение займа не может быть определен результат в старшем разряде. Этим объясняется низкое быстродействие вычитателей с последовательным переносом.

Таблица управления сумматора – вычитателя                                                     Таблица 8

Набор	Команды					Функции и числа
	K4	K3	K2	K1	K0
1	0	0	0	0	0	0
2	0	0	0	0	1	1
3	0	0	0	1	0	-1
4	0	0	0	1	1	0
5	0	0	1	0	0	-1
6	0	0	1	0	1	0
7	0	0	1	1	0	-2
8	0	0	1	1	1	-1
9	0	1	0	0	0	B
10	0	1	0	0	1	B + 1
11	0	1	0	1	0	–B – 1 = B’ (инверсия B)
12	0	1	0	1	1	–B
13	0	1	1	0	0	B – 1
14	0	1	1	0	1	B
15	0	1	1	1	0	–B – 2
16	0	1	1	1	1	–B – 1 = B’ (инверсия B)
17	1	0	0	0	0	A
18	1	0	0	0	1	A + 1
19	1	0	0	1	0	A – 1
20	1	0	0	1	1	A
21	1	0	1	0	0	– A – 1
22	1	0	1	0	1	– A
23	1	0	1	1	0	– A – 2
24	1	0	1	1	1	– A – 1 = A’ (инверсия A)
25	1	1	0	0	0	A + B
26	1	1	0	0	1	A + B + 1
27	1	1	0	1	0	A – B – 1
28	1	1	0	1	1	A – B
29	1	1	1	0	0	B – A – 1
30	1	1	1	0	1	B – 1
31	1	1	1	1	0	– A – B – 2
32	1	1	1	1	1	– A – B – 1

Сумматор является основным элементом Арифметико-логического устройства (АЛУ) микропроцессора и выполняет все арифметические операции (сумма, разность, умножение, деление и т.д.).