Сумматоры. Полусумматоры и полные сумматоры. Параллельный сумматор с параллельным переносом. Сумматор-вычитатель, страница 2

По данному алгоритму определяются переносы в старших разрядах. Функция переноса определяется за счет последовательной подстановки переносов всех младших разрядов. Дополнительные функции позволяют упростить аналитические выражения и реализацию сумматора (рис. 5).

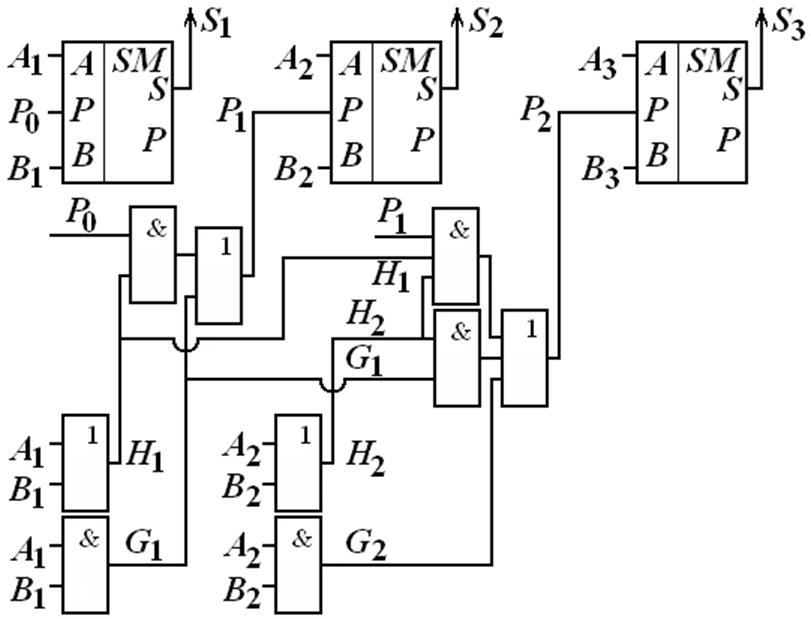
Рис. 5 Схема трехразрядного параллельного сумматора с параллельным переносом

Быстродействие сумматора велико, зависит только от времени формирования сигналов генерации, переноса, выполнения логической операции сложения и не зависит от разрядности сумматора.

С увеличением разрядности резко увеличивается количество используемых элементов и сложность схемы. Поэтому в много разрядных сумматорах используют последовательные, параллельные или другие виды переносов между группами разрядов. Внутри группы, обычно это четыре разряда, применяется параллельный перенос.

Вычитатель

Для выполнения операций вычитания, умножения и деления в цифровой технике используются сумматоры. При вычитании знак вычитаемого изменяется, и результат складывается с уменьшаемым двоичным числом.

Методы вычитания

а) В инверсном коде. Изменение знака получается инверсией всех бит разрядов вычитаемого. Если при сложении появляется единица в разряде, более старшем, чем разрядность вычитателя, то она прибавляется к младшему разряду результата.

Пример: вычесть 7 из 9, результат представить в двоичном коде.

Двоичное число	Десятичное число	Комментарий:
1001	9
1000	– 7	Инверсия кода 01112 = 710
1  0001		Сумма
0001		Перенос 1 из старшего разряда
0010	2	Результат: сложение суммы и переноса

Недостаток метода: представление ноля двумя способами, так как инверсия 0...00 равна 1. ..11 и сумма двух разных по знаку, но равных по значению чисел дает 1...11.

Пример: сложить 4 и – 4, результат представить в двоичном коде.

б) В дополнительном коде. Изменение знака получается инверсией всех бит разрядов числа, расширенного до полного формата и добавлением к результату 1 в младшем разряде. Единица в разряде, более старшем, чем разрядность вычитателя отбрасывается.

Вычитание в дополнительном коде можно применять не только в двоичной системе счисления. Например, стрелочные часы показывают 9 часов, а их надо установить на 1 час. Для этого часовую стрелку можно вращать против ее движения на 8 делений, что эквивалентно вычитанию, или по ходу на 4 деления, выполняя операцию сложения и получив тот же результат. В данном случае число 4 является дополнением к 8, а их сумма равна 12. Это справедливо только в случае, если нет переноса в следующий разряд (он отбрасывается).

Дополнение и вычитаемое число дополняют друг друга при n – разрядном представлении до  M ⁿ, где M – основание системы счисления.

Для указания знака числа используется старший (знаковый) разряд. У положительных чисел в этом разряде устанавливают значение, равное нулю, у отрицательных чисел равное единице.

При изменении знака значения всех бит разрядов двоичного числа расширенного до полного формата (в незаполненные старшие разряды записаны нули) заменяются дополнением до единицы (инвертируются),  и к результату добавляется 1 в младшем разряде. Единица в разряде, более старшем, чем разрядность вычитающего устройства отбрасывается.

Исключение единицы старшего разряда объясняется тем, что разрядность цифровых устройств ограничена и выходящие за эти ограничения по величине числа утрачиваются.

Пример: изменить знак числа 4 в двоичном коде (табл. 4).

Последовательность операции изменения знака                                       Таблица 4

Двоичное число		Десятичное число		Комментарий
знак	модуль	знак	модуль
0	0100	+	4	Положительное число
1	1011	–		Инверсия кода
0	0001	+		Единица младшего разряда
1	0100	–		Сумма инверсии и 1 младшего разряда
1	1100	–	4	Отрицательное число

Дополнение двоичного числа равно его отрицательному значению.

Необходимость добавления единицы младшего разряда объясняется тем, что обратный код выражается зависимостью:

 

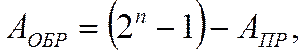
(3)

где: А_ПР – прямой код.

Например, 2₁₀ = 010₂, 2ⁿ -1 = 111₂. A_ОБР = 111 – 010 = 101.

Дополнительный код, по определению, равен:

 

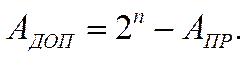(4)

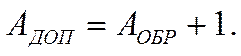Согласно (3, 4):

Пример: сложить четырехразрядные числа: 0001₂ =1₁₀ и код 1111₂:

11112	– 110	Из примера следует, что двоичный код 11112 соответствует                                – 110, т.к. сумма равна 0. Тогда меньшее на 1 значение                       11102 является  представлением – 210 и т.д.
00012	+110
00002	010

Пример: вычислить: 7 +(– 4), результат представить в четырехразрядном двоичном коде. Пятый разряд использовать как знаковый. Ответ в табл. 5.

Последовательность операции вычитания                                                 Таблица 5

Двоичное число		Десятичное число		Комментарий
знак	модуль	знак	модуль
0	0111	+	7	Первое слагаемое
0	0100	+	4	Вычитаемое в полном формате
1	1011	–		Инверсия вычитаемого
0	0001	+	1	Единица младшего разряда
1	1100	–		Сумма инверсии и 1 младшего разряда
1	1100	–	4	Второе слагаемое в дополнительном коде
0	0011	+	3	Сумма первого и второго слагаемых
0	0011	+	3	Результат вычитания

Если при добавлении дополнения в n – разрядном представлении отсутствует перенос в n +1 разряд, то результат является отрицательным числом.

Пример: числа в двоичном коде складываются и вычитаются аналогично методу расчета «в столбик» с учетом переносов и займов.

Где: A, B – четырех разрядные переменные, S₃ …S₀ – результат сложения; D₃ …D₀ – результат вычитания.

Пример: вычислить 4 +(–7), у полученной разности изменить знак, результат представить в четырехразрядном двоичном коде. Пятый разряд использовать как знаковый. Ответ в табл. 6.

Последовательность операции вычитания                                                Таблица 6