Сумматоры. Изучение работы полусумматора, и его таблицы истинности. Изучение работы полного сумматора, страница 2

Таблица истинности полувычитателя         Таблица 3

A0	B0	D0	E0
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

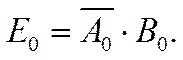
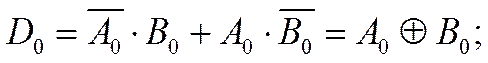Аналитические выражения выходных сигналов:

(2)

Примеры сложения и вычитания в двоичной системе счисления:

Для арифметического вычитания в одном разряде двоичной системы счисления используется логическая операция «Исключающее ИЛИ», для получения займа – логическая операция «Импликация».

3.2 Полный вычитатель

В этом устройстве определяется разница двух одноразрядных двоичных чисел с учетом займа в младший разряд – к значению вычитаемого прибавляется величина займа (0 или 1), и увеличенное вычитаемое вычитается из уменьшаемого.

Выходные значения: результат вычитания D и займ из старшего разряда E, рис. 6.

Функционально данная схема аналогична полному сумматору, состоит из двух полувычитателей и элемента ИЛИ для определения займа.

Контрольные точки D₁, E₁;D₂, E₂в схеме являются выходами первого и второго полувычитателя соответственно.

Задание 3

С помощью комбинаций входных логических сигналов изучить работу полного вычитателя (L2_add_08.ewb) и его таблицу истинности (рис. 6, табл. 4).

Обозначения на рис. 6: A _n – уменьшаемое, B _n – вычитаемое двоичные числа разряда n; D _n – результат вычитания в разряде n; E_n-1 – займ в младший разряд n-1. E_n – займ из старшего разряда n +1.

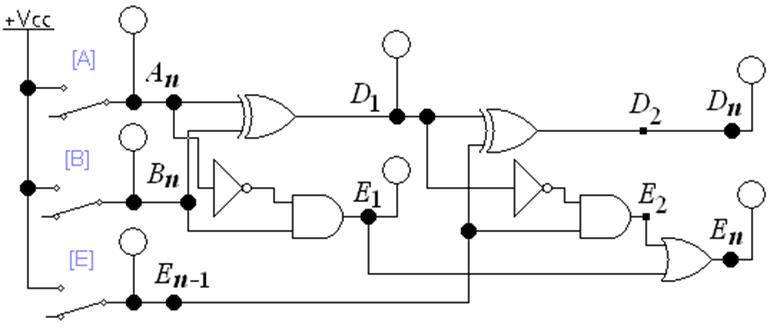
Рис. 6 Схема полного вычитателя

Таблица истинности полного вычитателя Таблица 4

An	B n	En-1	D n	En
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

Задание 4

С помощью двухразрядного сумматора (L2_add_05.ewb) и одноразрядного вычитателя (L2_add_08.ewb) провести расчеты и заполнить таблицы 5 и 6 соответственно. В них используются обозначения: двоичный код N₂, десятичное число N₁₀. Разрядность используемых в таблицах чисел определяется возможностями вычислительных устройств, наличием переносов и займов.

Таблица результатов сложения                                          Таблица 5

1-ое слагаемое			2-ое слагаемое			Результат
N10	N2		N10	N2		N10	N2
	A1	A0		B1	B0		Перенос	S1	S0
1	0	1	0	0	0
0	0	0	1	0	1
1	0	1	1	0	1
2	1	0	1	0	1
3	1	1	1	0	1
2	1	0	3	1	1
3	1	1	3	1	1

Таблица результатов вычитания                                       Таблица 6

Уменьшаемое		Вычитаемое		Займ		Результат
A n		B n		E n-1
N10	N2	N10	N2	N10	N2	N10	E n  (N2)	D n  (N2)
1	1	0	0	0	0
0	0	–1	1	0	0
0	0	0	0	–1	1
1	1	0	0	–1	1
1	1	–1	1	0	0
0	0	–1	1	–1	1

Знак «–» означает, что число вычитается из уменьшаемого.

4 Сумматор – вычитатель

Схема устройства сумматора – вычитателя со знаковым разрядом представлена на рис. 7, его команды управления K₀, K₀, K₂ в таблице 7.

На вход сумматора – вычитателя подаются в параллельном коде два разряда переменной A (A₁A₀) и два разряда переменной B (B₁B₀), старшие разряды A₁ и B₁ соответственно.

Для получения отрицательного двоичного числа все значения ее кода поразрядно инвертируются на элементах «Исключающее ИЛИ». Это происходит, если на один из входов данных элементов подать логическую единицу (команды К₁ = 1 или К₂ = 1), при К₁ = 0, К₂ = 0 инверсии нет.

К полученному инверсному значению добавляется единица в младший разряд с помощью команды К₀ = 1 согласно методу изменения знака в дополнительном коде.

Операция вычитания получается за счет сложения положительного и отрицательного чисел.

Выходные сигналы: результат расчетов младшего разряда S₀, результат расчетов  старшего разряда S₁, знак двоичного результата: L=0 положительное, L=1 отрицательное числа.

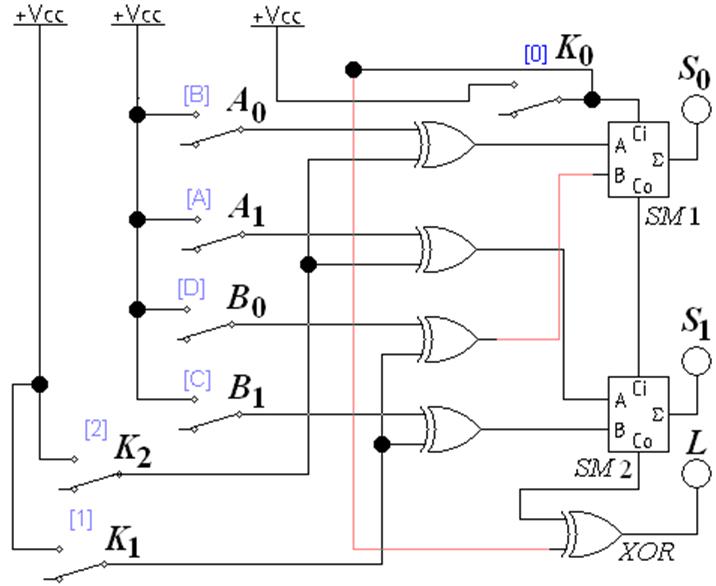
Рис. 7 Схема двухразрядного сумматора – вычитателя

со знаковым третьим разрядом (L2_add_09.ewb)

Таблица управления сумматора – вычитателя               Таблица 7

Набор	Функции и числа
	K2	K1	K0	Операция
1	0	0	0	A + B
2	0	1	1	A – B
3	1	0	1	B – A
4	1	0	0	инверсия A, если B = 0
5	0	1	0	инверсия B, если A = 0