Теорія поля. Основні поняття теорії поля. Скалярне поле. Векторне поле. Оператор Гамільтона (Теоретичний матеріал та контрольні завдання зі зразками вирішення з вищої математики)

4 ТЕОРІЯ ПОЛЯ

4.1 Основні поняття теорії поля

Теорія поля – розділ математики, в якому вивчаються скалярні, векторні, тензорні поля.

До розгляду скалярних і векторних полів приводять багато задач фізики, електротехніки, математики, механіки та інших технічних дисциплін. Вивчення одних фізичних полів сприяє вивченню й інших. Так, наприклад, сили всесвітнього тяжіння, магнітні, електричні сили — всі вони змінюються обернено пропорційно до квадрата відстані від свого джерела; вид силових магнітних ліній нагадує картину обтікання перешкод рідиною та ін.

Основними в теорії поля є такі поняття, як градієнт, потік, потенціал, дивергенція, ротор, циркуляція . Ці поняття важливі і в засвоєнні основних ідей математичного аналізу функцій багатьох змінних.

Полем називається область V простору, в кожній точці якої визначено значення деякої величини. Якщо кожній точці М цієї області відповідає певне число U = U(M), говорять, що в області визначено (задано) скалярне поле (або функція точки). Інакше кажучи, скалярне поле — це скалярна функція U(M) разом з її областю визначення. Якщо ж кожній точці М області простору відповідає деякий вектор а = а(М), то говорять, що задано векторне поле   (або векторна функція точки).

Прикладами скалярних полів можуть бути поля температури (повітря, тіла ...), атмосферного тиску, густини (маси, повітря ...), електричного потенціалу та ін.. Прикладами векторних полів є поле сили ваги, поле швидкостей частинок поточної рідини (вітру), магнітне поле, поле густини електричного струму та ін..

Якщо функція U(M)  не залежить від часу, то скалярне (векторне) поле називається стаціонарним ;поле, яке міняється з часом (міняється, наприклад, скалярне поле температури при охолоджуванні тіла), називається нестаціонарним .

Далі розглядатимемо тільки стаціонарні поля.

Якщо V — область тривимірного простору, то скалярне поле U можна розглядати як функцію трьох змінних х, у, z (координат точки М).

U = U(x;y;z).

Якщо скалярна функція U(M) залежить тільки від двох змінних, наприклад х і у, то відповідне скалярне поле U(x; у) називають плоским.

Аналогічно: вектор а = а(М),що визначаючає векторне поле, можна розглядати як векторну функцію трьох скалярних аргументів х, у і z: а = а(х; у; z) .

Вектор а = а(М) можна подати (розклавши його за ортами координатних осей) у вигляді

а = Р(х; у; z) i + Q(x; у; z) J + R(x; у; z) k,

де Р(х; у; z), Q(x; у; z), R,(x\ у; z) — проекції вектора а(М) на осі координат. Якщо у вибраній системі координат Oxyz одна з проекцій вектора а = а(М) дорівнює нулю, а дві інші залежать тільки від двох змінних, те векторне поле називається плоским. Наприклад, а = P(x;y) i + Q(x;y) j.

.

4.2 Скалярне поле

4.2.1 Поверхні та лінії рівня

Розглянемо скалярне поле, що задається функцією U = U(x;y;z). Для наочного представлення скалярного поля використовують поверхні та лінії рівня.

 Поверхнею рівня скалярного поля називається геометричне місце точок, в яких функція U(M) набуває постійного значення, тобто

U(x;y;z)= С.          

Задаючи у цій рівності величині С різні значення, одержимо різні поверхні рівня, які в сукупності ніби розшаровують поле. Через кожну точку поля проходить тільки одна поверхня рівня. Її рівняння можна знайти шляхом підстановки координат точки в рівняння .

Для скалярного поля, утвореного функцією U=поверхнями рівня є безліч концентричних сфер з центрами у початку координат: = С. Зокрема, якщо С=1, отримаємо  = 0,  тобто сфера стягується в точку.

У разі плоского поля U = U(x; у) рівність U(x; у)= С  є рівнянням лінії рівня поля, тобто лінія рівня —

це лінія на площині Оху, в точках якої функція U(x;y) зберігає постійне значення.            |

В метеорології, наприклад, мережі ізобар та ізотерм (лінії однакового середнього тиску та однакових середніх температур) є лініями рівня та  функціями координат точок місцевості.

Лінії рівня застосовуються в математиці при дослідженні поверхонь методом перетинів.

4.2.2 Похідна за напрямом

Для характеристики швидкості зміни поля U=U(Р) в заданому напрямку введемо поняття «похідної за напрямом».

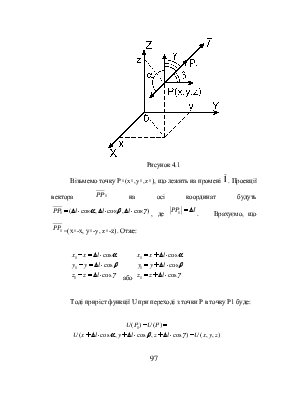
 Нехай задано скалярне поле U=U(x,y,z). Візьмемо в полі точку P(x,y,z) та промінь, що з неї виходить. Вектор  утворює з осями ОХ, ОY, OZ відповідно кути . Якщо =(lх, lу, lz), то направляючі косинуси вектора  будуть такими:

,  ,  .

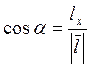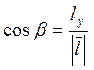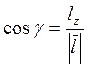Одиничний вектор

.

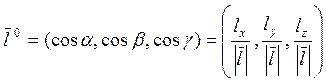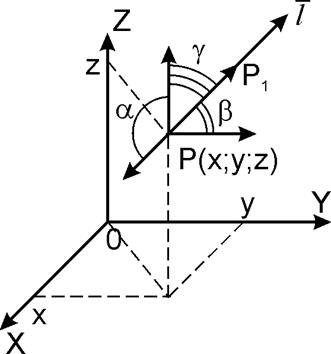
Рисунок 4.1

Візьмемо точку Р(x,y,z), що лежить на промені . Проекції вектора  на осі координат будуть , де .  Врахуємо, що =(х-х, y-y, z-z). Отже:

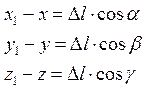  або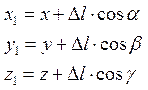 

Тоді приріст функції U при переході з точки Р в точку Р1 буде:

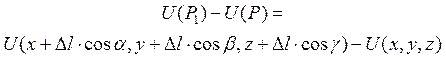
Оскільки повний приріст функції

,

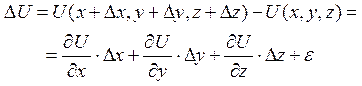де  - нескінченно мала величина більш високого порядку, ніж .  Якщо , , , то

_

,

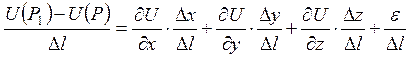де  .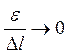

Тоді

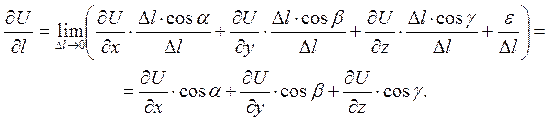
Отримали формулу для обчислення похідної за напрямом.

У разі плоского поля  U=U(x,y)  маємо

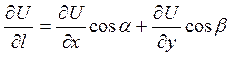
Зауваження. Поняття похідної за напрямом є узагальненням поняття  частинних похідних , , . Їх можна розглядати як похідні від функції і за напрямами координатних осей Ох, Оу і Oz. Так, якщо напрям l співпадає з додатним напрямом осі Ох, то, прийнявши 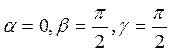 , отримаємо .

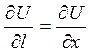 Приклад 4.1

Обчислити похідну функції U=ln(6x+7y) у точці М(-2;2) у напрямі вектора ММ, де М(2;-1)

Рішення

Знайдемо вектор ММ=(4;-3). . Знайдемо cos=, cos .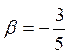

Обчислимо частинні похідні у точці М(-2;2):

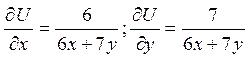. Звідси

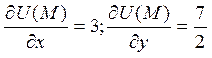. Знайдемо .

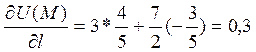Отже, дана функція в точці М зростає в напрямі ММ зі швидкістю 0,3.

4.2.3 Градієнт та його властивості

Градієнтом  поля називається вектор, проекції якого є значення частинних похідних функції, тобто

.

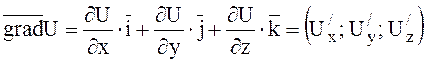  Напрям градієнта функції U(x,y,z) в кожній точці співпадає з напрямом нормалі до поверхні рівня скалярного поля, що проходить через цю точку, оскільки рівняння нормалі до поверхні рівня в точці :

.

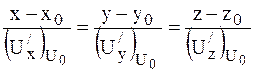 Градієнт направлений по нормалі до поверхні рівня (або до лінії рівня, якщо поле пласке).

 Градієнт направлений у бік зростання функції поля.

Наведемо деякі властивості градієнта:

1)  .

2)  .

3)  .

4)  .

Приклад 4.2

Знайти величину  і напрям градієнта  поля U=x+2y+3z+xy+3x-2y-6z     в точці В (2,0,1). В якій точці градієнт поля дорівнює нулю?

Рішення. Згідно з визначенням градієнта маємо:

grad U=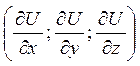=(2x+y+3; 4y+x-2; 6z-6).

grad U(B)=(7;0;0).

Прирівняємо значення градієнта функції до нуля і знайдемо точку, в якій градієнт обертається в нуль: 2х+у+3=0; 4у+х-2=0; 6z-6=0. Звідси  z=1, y=1, x=-2, тобто grad U=0, де М(-2;1;1).

4.3 Векторне поле

4.3.1  Векторні лінії поля

Розглянемо векторне поле, що задається вектором = {М). Вивчення поля зручно починати з поняття векторних ліній; вони є найпростішими геометричними характеристиками поля  Векторною лінією поля  називається лінія, дотична до якої в кожній її точці М має напрям відповідного їй вектора (М).

Це поняття для конкретних полів має ясний фізичний сенс. Наприклад, в полі швидкостей поточної рідини векторними лініями будуть лінії, вздовж яких рухаються частинки рідини (лінії струму); для магнітного поля векторними (силовими) лініями будуть лінії, що виходять з північного полюса і закінчуються в південному.

Сукупність всіх векторних ліній поля, що проходять через деяку замкнуту криву, називається векторною трубкою.

Вивчення векторного поля звичайно починають з вивчення розташування його векторних ліній. Векторні лінії поля

описуються системою диференціальних рівнянь виду

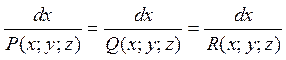                                              (4.1)

 Дійсно, нехай PQ  — векторна лінія поля,  = xi+yj+zk- її радіус-вектор. Тоді вектор dr = dx i + dy j + dz k має напрям дотичної до лінії PQ в точці М (див. рис. 4.2).

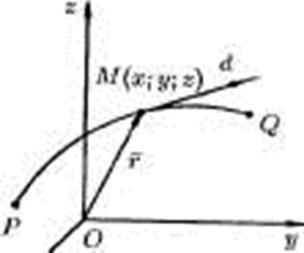
Рисунок 4.2

З колінеарності векторів  і dr випливає пропорційність їх проекцій, тобто рівність (4.1).

Приклад 4.3

Знайти  векторні лінії поля а=(y+z)i – xj – xk.

Рішення

Згідно до (4.1) маємо:

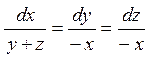       або          .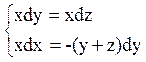

З першого рівняння системи отримуємо:

y-z=c, де с – довільна стала. Згідно рівності dy=dz, з другого рівняння системи знаходимо  (xdx+ydy+zdz=0) або (x+y+z=R), де R – стала.

Таким чином, рівняннями векторних ліній є лінії перетину сфер x+y+z=R та паралельних площин y-z=c, тобто кола.

4.3.2 Потік векторного  поля

Нехай векторне поле утворено вектором

 а = Р(х; у; z) l + Q(x; у; z) j + R(x; у; z) к.

 Для наочності вважатимемо а(М) вектором швидкості деякого потоку рідини, що рухається стаціонарно. Уявимо, що деяка поверхня S знаходиться в цьому потоці і пропускає рідину. Підрахуємо, кількість рідини що, протікає через поверхню S.

Виберемо певну сторону поверхні S. Нехай  п = (cos ; cos ; cos ) — одиничний вектор нормалі до даної сторони поверхні S. Розіб'ємо поверхню на елементарні майданчики  Si , S2 ,      , Sn.  Виберемо в кожному майданчику точку М (i =1,2..., п) (див. рис. 4.3) і обчислимо значення вектора швидкості  а(М) в кожній точці: а{М), а(М),     , а(М).