Определение времени возбуждения и самовозбуждения генератора постоянного тока и описание характеристики холостого хода

МИНИСТЕРСТВО    ОБРАЗОВАНИЯ  РФ

ВЯТСКИЙ  ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ

Кафедра  электрических машин  и  аппаратов

ОПРЕДЕЛЕНИЕ   ВРЕМЕНИ   ВОЗБУЖДЕНИЯ  И САМОВОЗБУЖДЕНИЯ  ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА  И  ОПИСАНИЕ  ХАРАКТЕРИСТИКИ  ХОЛОСТОГО ХОДА

Лабораторная работа  № 1

Дисциплина  “Математическая теория электрических машин”

Выполнили:                                                                         студенты гр. ЭМ-41

Ванюшкин И.А.

Гонин А.В.

Полубоярцев А.Е.

Проверил:

Шестаков А.В.

Киров  2005

1  Цель работы

Ознакомление с различными способами аппроксимации характеристики холостого хода машины постоянного тока, а также с методами аналитического решения дифференциальных уравнений генератора постоянного тока для процессов возбуждения и самовозбуждения.

2 Теоретические пояснения к работе

Процесс возбуждения, то есть нарастания напряжения на зажимах машины постоянного тока, является одним из самых распространенных переходных процессов, происходящих при ее нормальной эксплуатации. В ряде случаев при проектировании машины задаются скоростью протекания этого процесса и максимальным («потолочным») напряжением. Например, для возбудителей мощных синхронных генераторов скорость нарастания напряжения может превышать 2 относительных единицы (о.е.)  в секунду, а кратность форсировки (отношение «потолочного» напряжения к номинальному) – 1,8 о.е.

В настоящей работе предлагается сравнить между собой зависимости напряжения на якоре от тока возбуждения U_a=f(i_f) при различных допущениях, а также построить осциллограммы   U_a=f(t) по формулам, полученным в результате аналитического решения дифференциальных уравнений генератора постоянного тока при возбуждении и самовозбуждении с учетом нелинейной функции U_a=f(i_f).

2.1 Процесс возбуждения при ненасыщенной магнитной системе

В этом простейшем случае задачу нахождения зависимости U_a=f(t) можно решить из уравнений машины постоянного тока для режима холостого хода в операторной форме и системе относительных единиц:

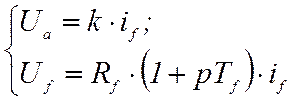,                                              (1)

где  U_a – напряжение на якоре;

U_f   – напряжение на обмотке возбуждения;

i_f  – ток возбуждения;

R_f – активное сопротивление обмотки возбуждения;

p– оператор дифференцирования;

k = νM_f , ν – относительная частота вращения, M_f – взаимная индуктивность обмоток якоря и возбуждения;

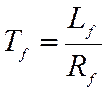 – постоянная времени обмотки возбуждения;

L_f – индуктивность обмотки возбуждения (рисунок 1).

Рисунок 1 – Электрическая схема генератора постоянного тока.

Отсюда для изображения функции  U_a:

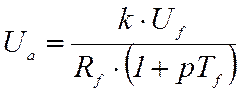.                                            (2)

 При переходе от изображения к оригиналу получается:

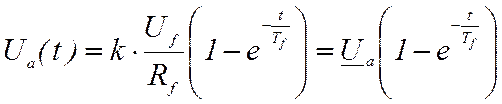,                             (3)

где 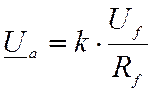 – установившееся значение напряжения на якоре (при t → ∞).

Таким образом, если к обмотке возбуждения вращающейся ненасыщенной машины внезапно подключается напряжение U_f , то напряжение на якоре будет изменяться по экспоненциальному закону с постоянной времени T_f. Уравнение (3) можно записать в форме, определяющей время возбуждения в зависимости от U_a:

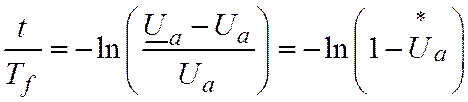,                          (4)

где 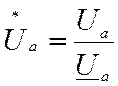 – напряжение на якоре в относительных единицах.

2.2 Процесс возбуждения от постороннего источника тока с учетом

                      реальной кривой намагничивания

Учет насыщения, то есть нелинейной зависимости U_a=f(i_f), делает решение задачи операторным методом невозможным. Поэтому применяется способ нахождения зависимости U_a=f(t), приведенный ниже.

В классической форме записи уравнение для цепи возбуждения имеет вид (в физических единицах):

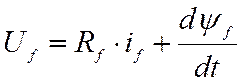,                                         (5)

где  ψ_f –полное потокосцепление обмотки возбуждения.

Если в качестве базисной единицы времени выбрать условную постоянную времени обмотки 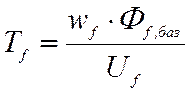возбуждения , где w_f  – число витков в обмотке возбуждения, Φ_f,баз  – магнитный поток, соответствующий установившемуся значению тока в обмотке возбуждения; в качестве базисного тока возбуждения 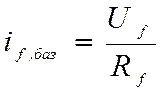, то, разделив соотношение (5) почленно на уравнение 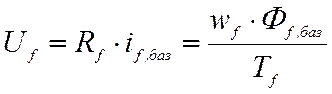, можно получить:

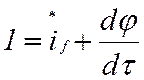,                                               (6)

где относительное время τ выражено в долях T_f , 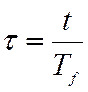;  – ток возбуждения в относительных единицах, 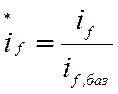; φ – относительное значение потока возбуждения, .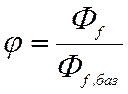

Зависимость 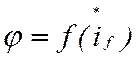, которая определяется кривой намагничивания машины, можно аппроксимировать ветвью гиперболы, проходящей через начало координат и точку с =1, φ=1:

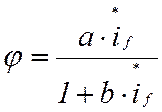,     откуда 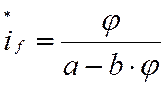    ,                       (7)

где a и b – коэффициенты, полученные в результате аппроксимации кривой намагничивания в виде гиперболы, причем, a=1+b.

Подставив это выражение в (6), получим дифференциальное уравнение

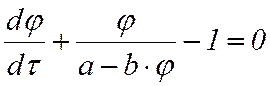,                                              (8)

которое легко разрешается относительно τ:

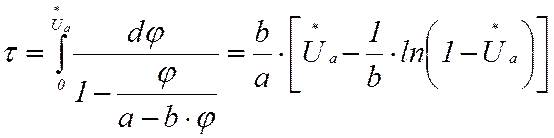,                        (9)

или

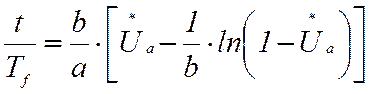.                                    (10)

Физически зависимость (10) определяет время в долях T_f, которое требуется для того, чтобы в процессе возбуждения напряжение на якоре генератора увеличилось от нуля до заданного напряжения, выраженного в долях установившегося значения U_a.

2.3 Процесс самовозбуждения

Исходным уравнением, описывающим этот процесс, будет уравнение для цепи возбуждения:

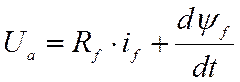,                                      (11)

отличающееся от уравнения (5) только левой частью, так как при самовозбуждении обмотка возбуждения подключается параллельно обмотке якоря, и ЭДС якоря равна напряжению U_a, поскольку падением напряжения на активном сопротивлении якоря можно пренебречь ввиду незначительности величины тока возбуждения.

Аналогично решению, приведенному в пункте 2.2, выбирая в качестве базисной единицы постоянную времени обмотки возбужденияT_f и учитывая, что в системе относительных единиц поток возбуждения равен напряжению на якоре, можно получить:

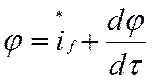.                                                        (12)

Заменяя зависимостью (7), получаем следующее дифференциальное уравнение:

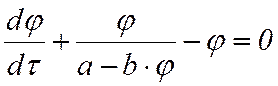.                                           (13)

Решая это уравнение относительно τ, можно найти искомую зависимость:

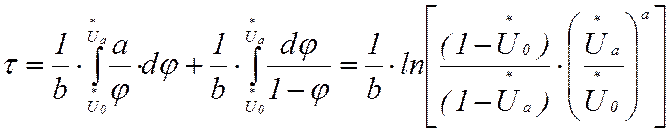.                  (14)

Здесь a и b – коэффициенты аппроксимации кривой намагничивания в виде гиперболы; 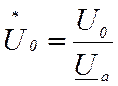, где   – напряжение на зажимах якоря, обусловленное потоком остаточного намагничивания. При 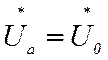(начало процесса самовозбуждения) τ=0. При 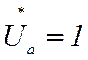  τ→∞.

Или для времени в физических единицах:

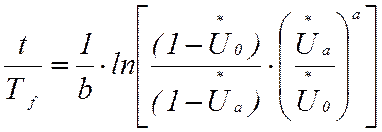.                            (15)

3 Программа работы

3.1 Характеристика холостого хода генератора постоянного тока U_a=f(i_f) при возрастании и убывании тока возбуждения.

Таблица 1 – Результаты эксперимента