НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И ИНЖЕНЕРнАЯ ГРАФИКА
Основой начертательной геометрии и инженерной графики является наука геометрия.
Геометрия изучает геометрические свойства геометрических примитивов, функциональные при геометрических преобразованиях.
Геометрические примитивы:
1. Точка
2. Отрезок прямой линии (прямая)
3. Отсек плоскости (плоскость)
4. Тело (простые геометрические тела)
Геометрические преобразования:
1. Перенос (параллельный)
2. Поворот
3. Масштабирование
4. Проецирование
Свойства геометрических примитивов:
Точка – координаты х,y,z
Прямая – длина, углы наклона – α,β,γ
Плоскость – площадь, длина периметра, координаты центра тяжести, углы наклона плоскости к плоскостям проекций - α,β,γ и пр.
Тело – объём, площадь поверхности, координаты центра тяжести и др.
Это собственные (абсолютные свойства), есть еще вторая группа свойств – свойства положения (относительные) -параллельность, перпендикулярность и пр.
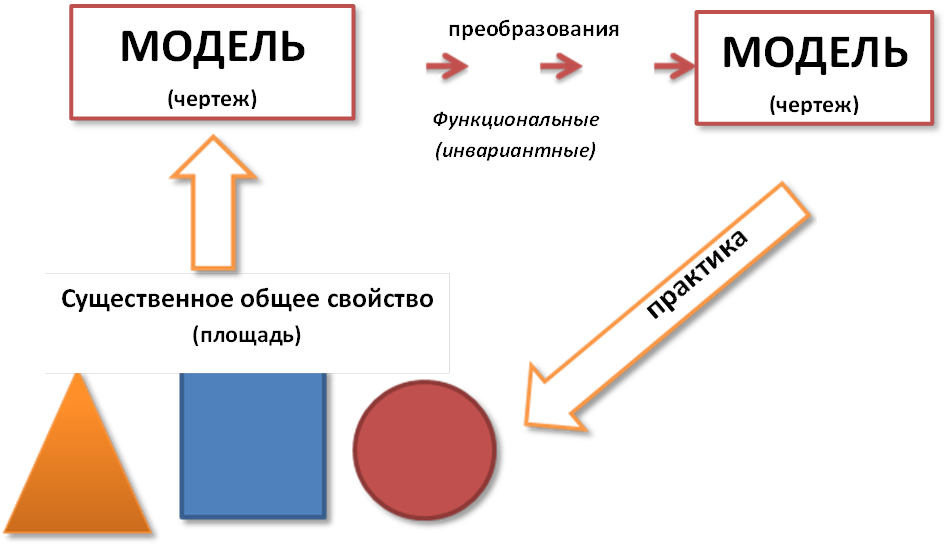
Основной научный метод – метод моделей.
Метод моделей
Типовые задачи геометрии
 |
![]()
![]()
![]()

![]()
![]()



![]()
 |
ТЗ-8 – точка + плоскость
![]()
![]()

![]()
![]() Типовая задача № 1
Типовая задача № 1 ![]() («задача штирлица»)
(«задача штирлица»)
 |
|||
 |
|||
Рис.1. Рис.2.
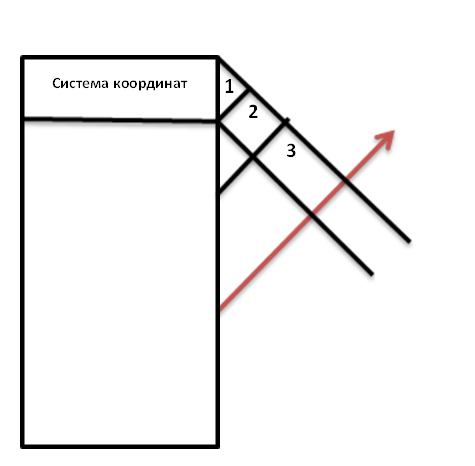
Точность построения на рис.1. максимальна, поэтому применяют прямоугольную
(ортогональную) систему координат. Поскольку ПОВОРОТ является инвариантным преобразованием, разворачивание всех трех плоскостей в одну плоскость образует т.н. комплексный чертеж.
Точность пеленгации места выхода в эфир передатчика разведчика выше на рис.1. (отсюда – «задача Штирлица»).
Первое правило Берикова – если в задаче участвуют примитивы «соседних» размерностей, размерность одного из них понижается (повышается) до размерности второго (как правило, с помощью двукратной (однократной) замены плоскости проекции)
Второе правило Берикова – если в задаче участвуют примитивы «не соседних» размерностей, задача решается с помощью примитива-посредника промежуточной размерности.
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() Типовая
задача № 2 (точка в системе плоскостей проекций)
Типовая
задача № 2 (точка в системе плоскостей проекций)
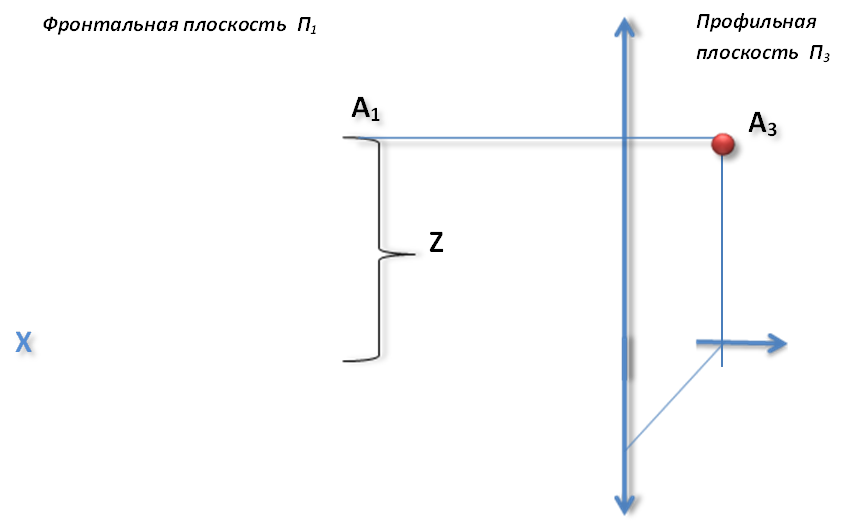 |
![]()
 |
|||||
 |
|||||
Рис.3. Типовая задача № 2
Для определения координат точки – достаточно двух проекций
Прямые разделяются на три типа – два типа прямых частного положения (проецирующие и прямые уровня) и прямые частного положения.
Прямые, перпендикулярные какой-либо плоскости проекции, называются проецирующими. Например – горизонтально-проецирующая прямая – это прямая, перпендикулярная горизонтальной плоскости проекции.
![]()
![]()
![]() А1
А1
![]()
![]()
![]() В1
В1
![]() А2=В2
А2=В2
Рис.4. Горизонтально-проецирующая прямая
Поскольку отрезок прямой перпендикулярен одной плоскости проекций, он автоматически параллелен двум другим плоскостям проекций и на них проецируется в натуральную величину. Углы наклона в данном случае равны:
α = 0o
β = 900
γ = 0o
Отрезок прямой линии параллельный какой-либо плоскости проекции, называется прямой уровня и имеет название такое же как и плоскость, которой он параллелен. На ту плоскость, которой отрезок параллелен, он проецируется в натуральную величину. Углы наклона отрезка ко всем плоскостям проекций легко измеряются на чертеже (модели) без каких-либо преобразований.
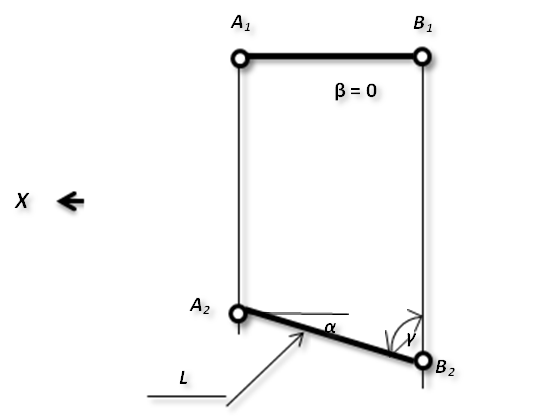 |
Рис.4. Горизонтальная прямая
Прямая, расположенная в пространстве под произвольными углами к плоскостям проекций называется прямой общего положения и для измерения длины отрезка и углов его наклона к плоскостям проекций требуются преобразования чертежа (модели). Для определения натуральной величины отрезка прямой применяются несколько методов преобразования чертежа:
1. Метод вращения;
2. Метод прямоугольного треугольника;
3. Метод замены плоскости проекции.
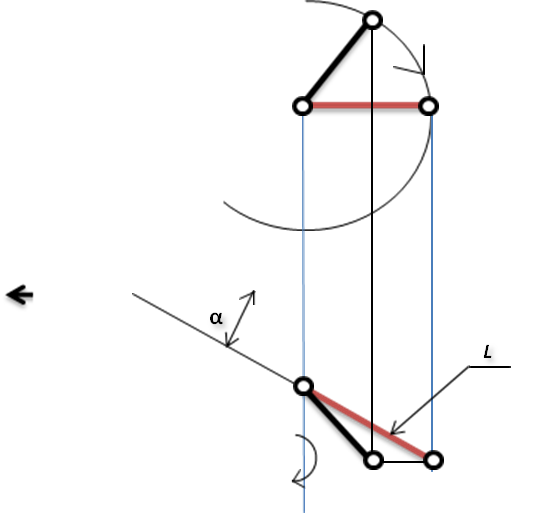
Практически все эти методы являются модификациями использования преобразования – «ВРАЩЕНИЕ». Так, например, вращение отрезка вокруг оси Z не изменяет длину отрезка L и угол наклона его к горизонтальной плоскости проекции β. Поэтому, для определения длины отрезка и угла наклона β используют вращение отрезка вокруг вертикальной оси. Углы наклона к другим плоскостям проекций определяют вращением отрезка прямой вокруг осей, параллельных другим осям координат. При вращении отрезка вокруг оси, параллельной оси Х не меняется (инвариантен) угол γ - угол наклона к профильной плоскости проекции. При вращении отрезка вокруг оси, параллельной оси Y не меняется угол наклона к фронтальной плоскости проекции α. Пример решениятакой задачи приведен на рис.5.
 |
|||
Рис.5. Определение длины отрезка и угла наклона α
методом вращения
 |
|||
 |
|||
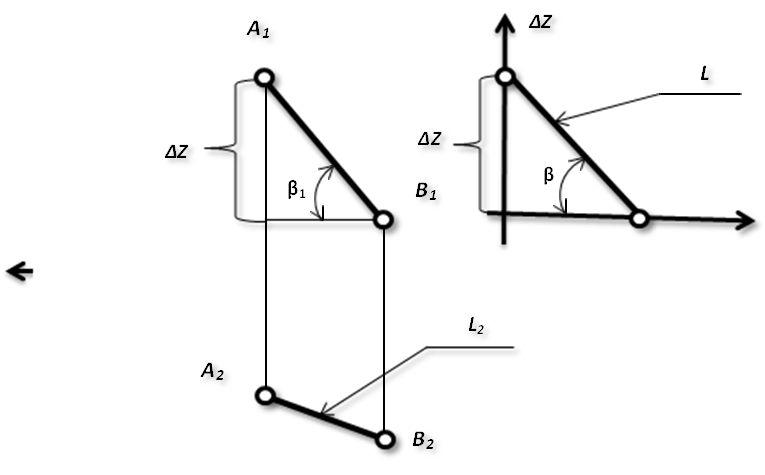
Рис.6. Определение параметров отрезка методом
«прямоугольного треугольника»
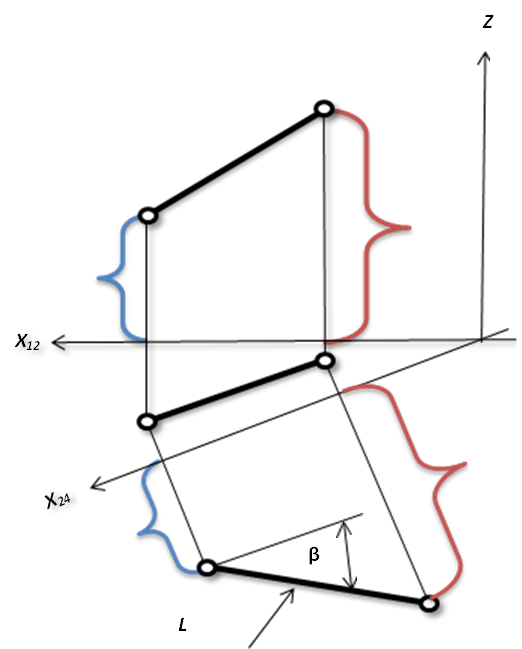 |
Рис.7. Определение L и β методом замены плоскости проекции
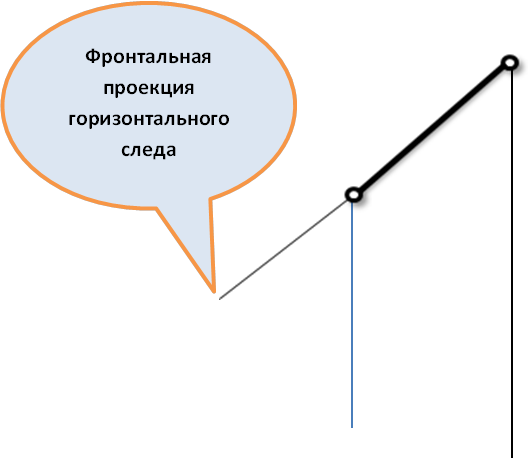
СЛЕДЫ ПРЯМОЙ ЛИНИИ. Следом прямой линии называется точка пересечения прямой с плоскостью проекции.
 |
![]() Х12
Х12
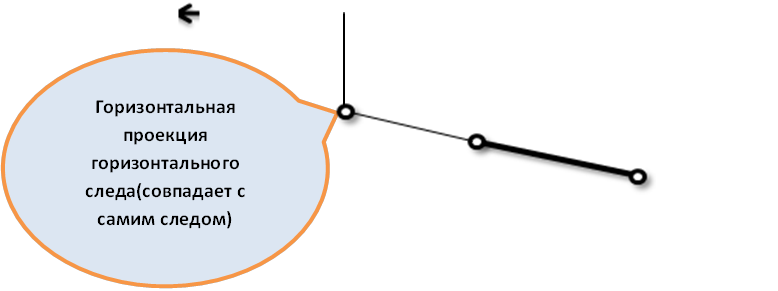
Рис.8. Построение горизонтального следа прямой линии.
Аналогично выглядят построения при определении фронтального следа
прямой линии.
 |
|||
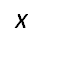 |
|||
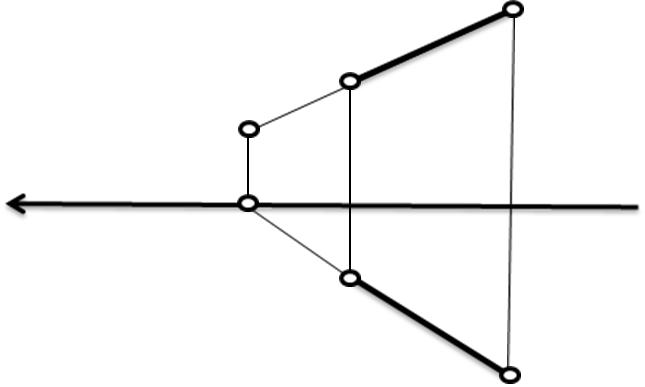
Рис. 9. Построение фронтального следа прямой линии
(подписать след и его проекции самостоятельно).
ТИПОВАЯ ЗАДАЧА № 4 «Плоскость в системе плоскостей проекций»
Плоскости, как и отрезки прямых линий, могут занимать как частное
( проецирующие и уровня ), так и общее положение.
СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ:
1. Тремя точками;
2. Плоской фигурой;
3. Двумя параллельными прямыми;
4. Двумя пересекающимися прямыми;
5. Следами.
Первые четыре способа легко перезадаются из одного способа в другой. Несколько особняком стоит вопрос перезадания следами.
Следами плоскости называются линии пересечения плоскости с плоскостями проекций. Чтобы построить след плоскости, нужно построить одноименные следы двух пересекающихся или параллельных прямых, лежащих в этой плоскости и соединить их прямой линией. При правильном построении следы плоскости пересекаются на оси Х в одной точке (!)


К1
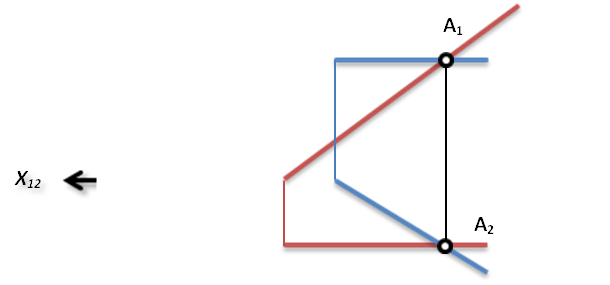 |
К2
Рис. 10. Плоскость К, заданная следами. Точка А принадлежит плоскости
В чертеже на рис.10. ясно видно, что горизонтальный след плоскости К2 и горизонтальная проекция горизонтальной линии (горизонтали) ПАРАЛЛЕЛЬНЫ !!! Аналогично – параллельны фронтальный след плоскости К1 и фронтальная проекция фронтали.
В решении типовой задачи № 4 обычно преобразуют чертеж для:
· Получения натуральной величины плоской фигуры;
· Измерения углов наклона плоскости к плоскостям проекций α,β,γ;
В числе способов преобразования чертежа используют:
· Замену плоскости проекции;
· Вращение геометрического примитива.
Чертежи вариантов решения типовой задачи № 4 выполнить самостоятельно.
Типовая задача № 5 «Тело в системе плоскостей проекций»
Каждое элементарное тело проецируется на комплексном чертеже в одной (нескольких) проекциях в зависимости от решаемой задачи, но как правило, в таких проекциях, которые позволяют проставить поэлементные размеры (размеры, задающие само элементарное геометрическое тело).
Цилиндр
 |
Рис.11. Изображение цилиндра
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.