Линейное пространство с операциями, определенными в n-мерном арифметическом пространстве. Определение линейно зависимых векторов пространства

1.1.  Является ли действительным линейным пространством с операциями, определенными в n-мерном арифметическом пространстве, множество n-мерных строк ( a₁ ,a₂,…,a_n) , a_i   , i=1,…,n, у которых

      1.1.1. все координаты равны между собой;

      1.1.2 первая координата  a₁ равна нулю;

      1.1.3 сумма координат равна нулю;

      1.1.4 сумма координат равна единице;

      1.1.5 координата a_n  равна сумме всех остальных координат;

      1.1.6 последняя координата  a_n  равна нулю?

1.2. Докажите, что множество решений однородной системы линейных уравнений образует линейное пространство над     : 

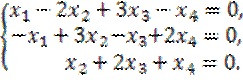
1.3. Исследуйте, являются ли векторы ₁=(-1,1,1,0), ₂=(2,-1,1,3), ₃=(-1,2,1,5), ₄=(2,2,-1,1) пространства     линейно зависимы. В случае утвердительного ответа найдите нетривиальную линейную комбинацию, равную нулю.

1.4. Исследуйте, является ли линейно зависимой система векторов пространства   [a,b]:

   1.4.1.  sin x, cos x;

  1.4.2. , ,  ;

  1.4.3. x, , x;

1.5. Исследуйте, являются ли векторы f₁(x)=+5, f₂(x)=-4x+3, f₃(x)=+16x+1   векторного пространства [x] линейно зависимы. В случае утвердительного ответа найдите нетривиальную линейную комбинацию, равную нулю.

1.6.    Найдите все значения     , при которых вектор =(1,1,2,)  линейно выражается через векторы  ₁=(1,2,3,-1), ₂=(0,1,-2,3), ₃=(-1,2,0,4).

1.7. Докажите, что линейные пространства V₁ и V₂ изоморфны.

   1.7.1.  V₁=M(2,)  ,  V₂=[x].

   1.7.2.  V₁=M(2,)  ,  V₂=.

  1.7.3.   V₁=[x]     ,  V₂=.

2.1. Докажите, что в линейном пространстве многочлены 1,…,  образуют базис; найдите координаты многочлена f(x)=-2+5-4   в этом базисе.

2.2. Докажите, что система векторов e₁=(1,1,1), e₂=(1,1,2), e₃=(1,2,3) образует базис в пространстве , и найдите координаты вектора a=(6,9,14)  в этом базисе .

2.3. Докажите, что матрицы Е₁= , Е₂= , Е₃= , Е₄=  образуют базис пространства  M(2,  , и запишите разложение вектора А=  по векторам этого базиса.

2.4. Даны векторы e₁=(2,1,-3), e₂=(3,2,-5), e₃=(1,-1,1), ₁=(0,1,-2), ₂=(-2,0,3), ₃=(1,-1,1) линейного пространства .

   2.4.1. Докажите, что векторы e₁ ,e₂ , e₃      и     ₁ , ₂ ,  ₃   образуют базис в пространстве .

   2.4.2. Найдите матрицу перехода от базиса  e₁ ,e₂ , e₃ к базису  ₁ , ₂ ,  ₃   .

   2.4.3. Найдите матрицу перехода от базиса  ₁ , ₂ ,  ₃   к базису  e₁ ,e₂ , e₃ .

   2.4.4. Найдите координаты вектора  =(2,0,1) в базисе e₁ ,e₂ , e₃ .

   2.4.5. Найдите координаты вектора  x= e₁ - e₂ +2 e₃  в базисе  ₁ , ₂ ,  ₃   .

3.1. Выясните, является ли подпространством линейного пространства  M(n,) множество К:

  3.1.1. невырожденных матриц порядка n;

  3.1.2. вырожденных матриц порядка n;

  3.1.3. квадратных матриц порядка n с определителем 1?

3.2. Найдите размерность и базис линейной оболочки  L(₁ , ₂ ,  ₃  , ₄) системы векторов из , где ₁=(1,0,0,-1), ₂=(2,1,1,0), ₃=(1,1,1,1), ₄=(1,2,3,4).

3.3. Найдите размерность и базис линейной оболочки  L(₁ , ₂ ,  ₃  )  векторов из [x] , где ₁=+x+1, ₂=-x, ₃= -2x-1.

3.4. Найдите размерность и базис суммы, а также размерность пересечения подпространств  L(₁ , ₂ ,  ₃  )  и L(b₁ ,b₂)   линейного пространства ,где ₁=(1,-1,2), ₂=(3,0,2), ₃=(2,1,0), b₁=(1,1,3), b₂=(0,1,2),. Выяснить, принадлежит ли вектор x=(1,3,5) пространствам L(₁ , ₂ ,  ₃  )  , L(b₁ ,b₂) ?

3.5. Пусть в пространстве  А= L(₁ , ₂  ) , В= L(₃ , ₄  ). Докажите, что   =А В . Представьте вектор x в виде x= x₁ + x₂ , где x₁ А, x₂  В, ₁=(1,1,-1,-1), ₂=(3,-1,1,-2),₃=(2,1,2,-3), ₄=(1,2,3,-3), x=(0,2,0,-1).