Синтез и анализ системы автоматического регулирования, страница 3

Дополнительные данные:

ρ_стали = 7,8·10³ кг/м³

с_стали = 500 Дж/кг*град

с_{капрона} = 1340 Дж/кг*град

Разработка математической модели объекта

Математическая модель объекта базируется на описании его динамики дифференциальным уравнением:

где         С_об – теплоемкость объекта, Дж/град;

              θ – текущая температура объекта, град;

              Q_под – подача тепловой энергии, Вт;

              Q_потр – потребление тепловой энергии, Вт.

Теплоемкость объекта определяется исходя из его геометрических и теплофизических характеристик:

где        с_стали – удельная теплоёмкость стали, Дж/кг*град;

              m_об – масса объекта, кг.

В свою очередь с_стали – это табличное значение, а масса объекта определяется как:

где         , м³;

, кг/м³.

Подача тепловой энергии осуществляется с подводимой к нему мощностью и является регулирующим воздействием.

Потребление тепловой энергии складывается из теплоотдачи (основной) в окружающую среду и дополнительной теплоотдачи. Первая определяется выражением:

 (4)

где         α – коэффициент теплоотдачи, Вт/град;

              F – площадь поверхности теплоотдачи, м²;

              θ – текущая температура объекта, град;

              θ_о.с. – температура окружающей среды, град.

Площадь поверхности теплоотдачи для термоэлектропластификатора будет равна площади его поверхности:

Вторая (дополнительная теплоотдача) Q_{потр. доп.} определяется конкретным объектом.

В случае термоэлектропластификатораQ_{потр. доп.} определяется теплоотводом в нагреваемую нить, нагрев которой происходит от температуры окружающей среды до температуры объекта:

где     m – линейная плотность нити, г/км;

          V – линейная скорость нити, м/с;

          c_k – удельная теплоемкость капрона, Дж/кг*град;

          θ – текущая температура объекта, град;

          θ_о.с. – температура окружающей среды, град.

В конечном итоге уравнение объекта должно принять вид:

где        T_о – постоянная времени объекта, с;

              k_о – коэффициент передачи объекта, град/Вт.

Уравнение датчика принимаем в виде:

где        T_д - тепловая инерция датчика, с.       

Выведем уравнение для нашего объекта:

Подставим в уравнение формулы (2), (4) и (6):

Подставим в уравнение формулу (3) и разделим на:

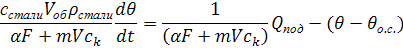
Подставим объём объекта:

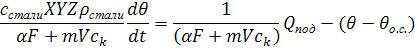
Подставим в уравнение формулу (5):