Проектирование железобетонного моста под железную дорогу через постоянный водоток в Новосибирской области, страница 8

  Расчет наклонных сечений по изгибающему моменту производим, используя следующее условие:

  ,            (2.65)

  где  - момент относительно оси, проходящей через центр сжатой зоны наклонного сечения, от расчетных нагрузок, М=1249,69кНм; , ,  - расстояние от усилий в ненапрягаемой арматуре до точки приложения равнодействующей усилий в сжатой зоне бетона в сечении, для которого определяется момент.

;

.

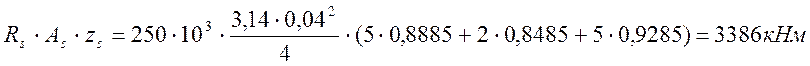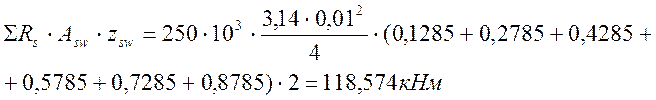
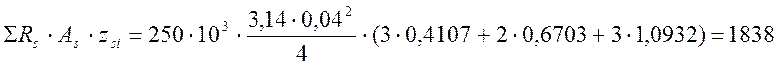1249,69кНм < 5343 кНм.

Условие выполняется.

2.2.10 Расчёт наклонного сечения балки по раскрытию трещин.

   Железобетонные балки с ненапрягаемой арматурой должны удовлетворять категории требований по трещиностойкости. Максимальные растягивающие напряжения  в поперечной и продольной арматуре определяем по формуле:

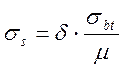  ,                       (2.66)

  где  -  напряжение в балке, равное касательному напряжению  на уровне центра тяжести сечения:

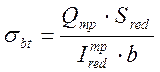  ,                      (2.67)

  где  - поперечная сила, определяемая по интерполяции на расстоянии (2ho + 0.35)=2,6м, =752,25кН;  - статический момент отсеченной части сечения, =0,469;  - приведенный момент инерции сечения, =0,296;  - коэффициент армирования стенки на участке наклонной трещины по направлению главных растягивающих напряжений:

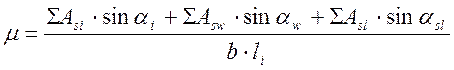  ,           2.68)

   - коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных трещин, определяемый по формуле:

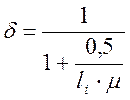,                       (2.69)

  где   - длина, см, предполагаемой наклонной трещины по направлению, перпендикулярному главным растягивающим напряжениям на участке между вутами поясов (см. Рис. 2.8), =140,86см.

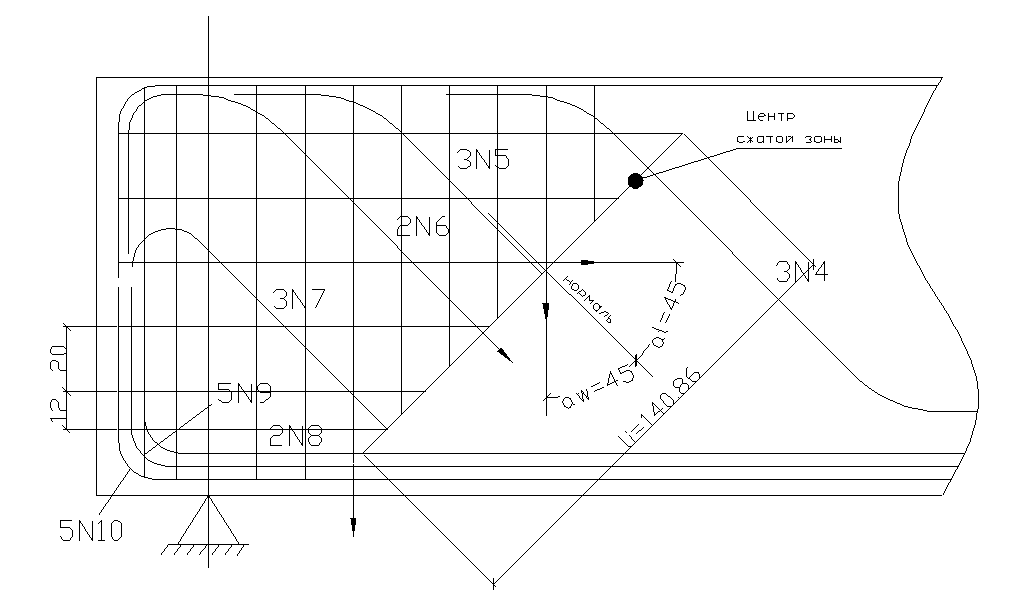 Рис. 2.8 Схема расчёта наклонного сечения на раскрытие трещин.

   Произведем вычисления:

;

;

;

;

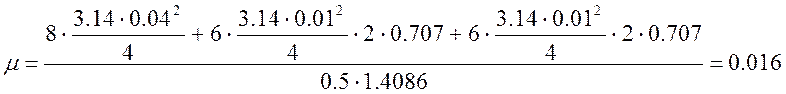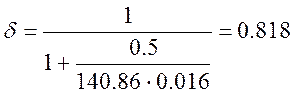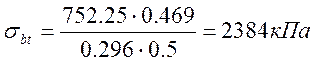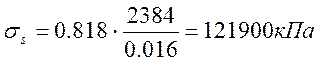  По условию (2.59) определяем радиус армирования по формуле:

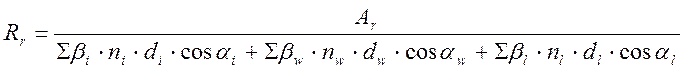  ,      (2.70)

  где площадь зоны взаимодействия вычисляем по формуле:

  ,                         (2.71)

 м²;

;

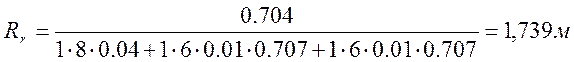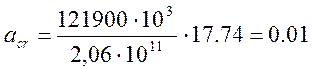 см;

см;

  0,01 см < 0,02 см.

  Условие по раскрытию трещин наклонного сечения выполняется.

2.2.11 Определение прогиба балки в середине пролёта

  Прогиб в середине пролета определяем по формуле:

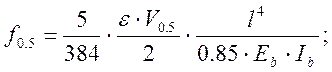                  (2.72)

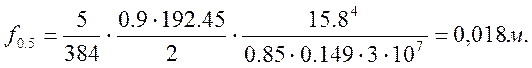
   Проверим выполнение условия: ,

  где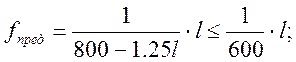

  

 

 

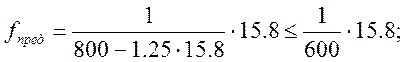
  Условие по ограничению прогиба  в середине пролета выполняется.

2.3 Расчет  обсыпного устоя.

  В данном курсовом проекте принимаем к расчету не обсыпной монолитный бетонный устой на массивном основании, запроектированный по второму варианту. Ширина по высоте устоя остается постоянной (3,1 м), тротуары вынесены на консоли.

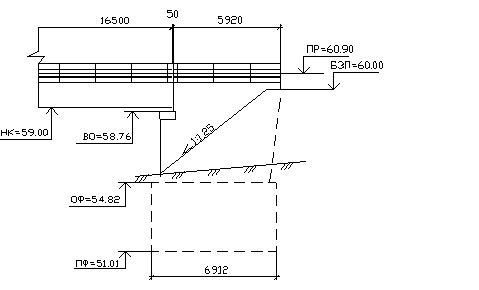
Рис. 2.9 Схема обсыпного устоя, принятого для расчёта.

2.3.1 Определение нагрузок.

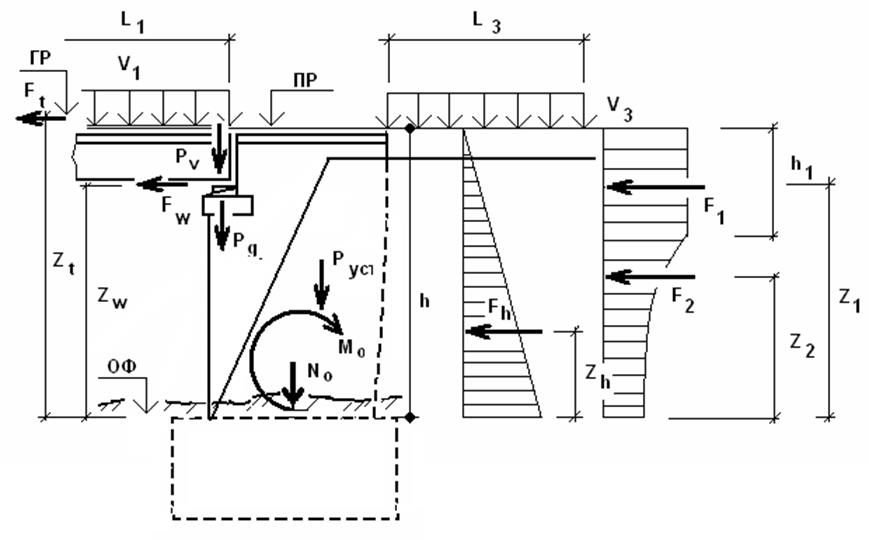
Рис. 2.10 Расчётная схема устоя при загружении в пролёт.

  Постоянные нагрузки:

  - Нагрузку от собственного веса устоя определяем по формуле:

  ,                          (2.73)

  где V – объем всего устоя (определим при помощи ЭВМ), V = 112 м³;  = 23.5 кН/м3 – удельный вес бетона.

кН.

  Положение центра тяжести устоя и точка приложения силы Р вычисляем при помощи ЭВМ.

  - Нагрузка от веса пролетного строения. На устой опирается  пролетное строение длиной 16.5 м, весом 492 кН с тротуарами и перилами общим весом 161,7 кН:

 кН.

  - Нагрузку от веса мостового полотна определяем по формуле:

,                        (2.74)

  где - распределенная нагрузка от веса балласта с частями пути;  - длина пролетного строения.

кН.

  - Нагрузка от веса балласта на устое

 кН;

  - Нагрузка от веса перил и тротуаров на устое

 кН.

   Временные нагрузки:

  - Эквивалентную нагрузку от подвижного состава на ПС определяем по приложению Н [1] при  и длине загружения  м:

 кН/м;

  Тогда нормативное вертикальное давление от временной нагрузки на ПС:

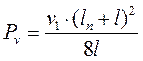;                       (2.75)

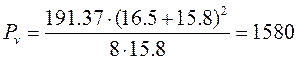кН.

  - Эквивалентную нагрузку на призме обрушения определяем исходя из длины загружения призмы обрушения, вычисляемой по формуле:

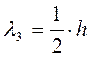  ,                           (2.76)

  где h – расстояние от подошвы рельса до обреза фундамента.

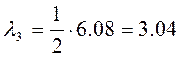 м; ;

 кН/м.

  - Горизонтальное давление от подвижного состава на призме обрушения определяем по формуле:

         (2.77)                

  где  - давление распределенной на длине шпал (2.7 м) временной вертикальной нагрузки, кН:

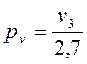;                         (2.78)                                             

Согласно (2.78) получим:

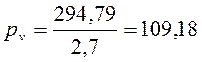 кН;

  b – ширина устоя (b = 3,1 м);

   - коэффициент нормативного горизонтального (бокового) давления грунта засыпки, определяемый по формуле:

,                     (2.79)                                      

где  - нормативный угол внутреннего трения грунта ().

Согласно (2.79) получим:

;

  Коэффициенты  в зависимости от высот h =6.08м и h1=b-2.7=0.4м (высота, в пределах которой площадь давления имеет переменную ширину) (рис. 2.10) определяем по табл.5.1, [1]:

.

  Подставляя значения в уравнение (2.79), получим:

F = 31.955 + 259,293 = 291,248 кН.

  Плечи сил  и , определяем по формулам:

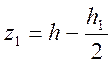;                         (2.80)                                                         

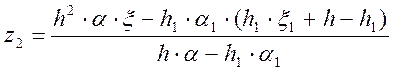;              (2.81)                                

  Согласно (2.80)-(2.81) получи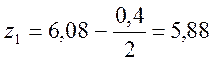м:

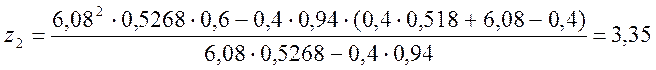 м;

 м.

  - Ветровую нагрузку вычисляем по формуле:

,                   (2.82)

  где =1.3м - высота балки;

  -толщина мостового полотна;

  -скоростной напор ветра;

  - коэффициент, учитывающий ветровое давление на определенной высоте;

  - аэродинамический коэффициент лобового сопротивления пролетного строения.

Согласно (2.82) получим:

.

  - Нагрузка от торможения подвижного состава:

;                            (2.83)                                             

  При этом, величина v₁определяется при λ₁=lп и a₁=0.5.

  Согласно (2.83) получим:

кН.

  - Давление грунта на заднюю стенку устоя:

  Напряжения в грунте на расчетном уровне, равно:

;                       (2.84)                                                                           

  где  - удельный вес грунта насыпи;

  z = 5.18 м - глубина расчетного уровня (расстояние от БЗП до ОФ).

  Согласно (2.84) получим: