Проектирование железобетонного моста под железную дорогу через постоянный водоток в Новосибирской области, страница 5

а_s = 0,5· d +0,02м,                       (2.16)

где d = 0,012 – диаметр стержня, м.

а_s = 0,5· 0,012 + 0,02 = 0,026 м.

Расчетную высоту сечения находим по формуле:

h = d₁ + 0,3·R,                         (2.17)

где d₁ = 0,15 толщина плиты, м;

R=0,3м – радиус вута, м.

h= 0,15 + 0,3·0,3 = 0,24 м.

Рабочую высоту сечения  вычисляем по формуле:

h₀ = h - а_s,                                    (2.18)

h₀ = 0,24 – 0,026=0,214 м.

Требуемую площадь сечения рабочей арматуры вычисляем по формуле:

 

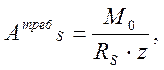(2.19)

z – плечо внутренней пары сил, определяемое по формуле:

 

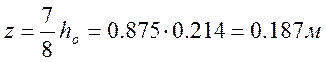(2.20)

M – расчётный момент в сечении, М=49.84кНм;

R_S - расчетное сопротивление арматуры, для AII R_S=250МПа;

 

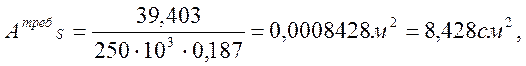(2.21)

Назначаем необходимое число арматурных стержней n:

Принимаем стержень класса АII с диаметром 12 мм. (А^1ст_s = 1,131см²)

 

(2.22)

 

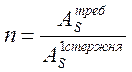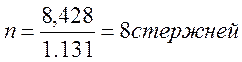2.1.7 Расчёт нормального сечения плиты на прочность.

    Результатом выполнения расчёта по прочности является проверка выполнения условий по следующим формулам:

а) на прочность по изгибающему моменту:

М_о £m_b7×R_b×b×x×(h_o – 0,5×x),                  (2.23)

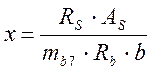где М_о = 39,403 кН·м; m_b7 = 0,9 – коэффициент условий работы, принимаемый по [2] п.3.25; R_b = 11,75 МПа – расчетное сопротивление бетона класса В22,5 сжатию; b = 1 м – толщина сечения; х – высота сжатой зоны, вычисляемая по формуле:

(2.24)

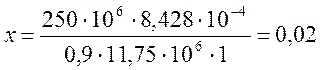м;

39,403 < ;   

39,403 кН < 45,192 кН.

Условие выполняется.

б) на прочность по поперечной силе:

                                                     Q £ 1,5×R_bt×h_o;                                            (2.25)

где R_bt = 1,90 МПа – расчётное сопротивление бетона на осевое растяжение.

123,136< ;

123,136 кН < 288,9 кН.

Условие выполняется.

2.1.8 Расчёт нормального сечения плиты на выносливость.

Расчет на выносливость сводится к ограничению напряжений в бетоне и арматуре соответствующими расчетными сопротивлениями. Расчет производится по формулам сопротивления материалов без учета работы бетона растянутой зоны. Условия выносливости имеют следующий вид:

а) Расчёт на выносливость по бетону:

Проверку на выносливость по бетону выполняем из условия:

 

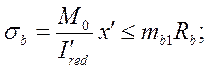 (2.26)

где s_b¢ – напряжение в бетоне;

М₀=39,403кНм;

х¢ – высота сжатой зоны бетона, определяемая по формуле:

 

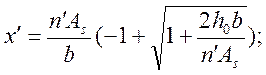(2.27)

n΄ - условное отношение модулей упругости арматуры и бетона  принимается: для бетона класса В22,5 равным 20 ([2]п.3.48).

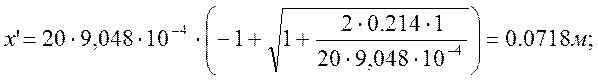
I_red – момент инерции приведённого сечения относительно его центра тяжести, определяется по формуле:

 

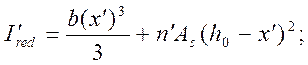(2.28)

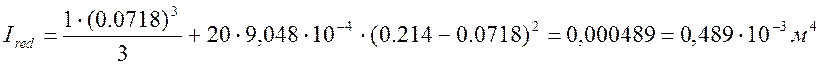
    m_b1 – величина определяется по формуле:

m_b1 = 0,6 ×b_b×e_b;                       (2.29)

    где b_b = 1,34 – коэффициент, учитывающий рост прочности бетона во времени, ([2]п.3.26);

    e_b – коэффициент, зависящий от коэффициента асимметрии цикла r_b, ([2]п.3.26):

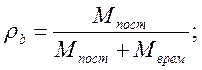                                         (2.30)

где М_пост = 2.76кН×м – момент на выносливость от постоянных нагрузок; (М_пост + М_врем)=27.291кН×м – момент на выносливость от постоянных и временных нагрузок (определяем по формуле 2.13).

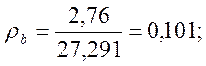
    Значит e_b=1.001.

m_b1 = 0,6×1,34×1,001=0,805.

 

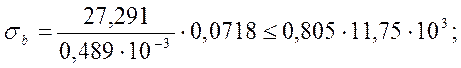Условие выполняется.

б)Расчёт на выносливость по арматуре выполняем из условия:

 

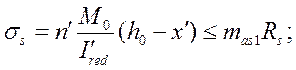    (2.31)

    где ss¢ – напряжение в арматуре;

    m_as1 – коэффициент условий работы арматуры по п.3.39 [2]:

                           m_as1 = b_rw × e_rs,                                         (2.32)

    где b_rw = 1 – коэффициент, учитывающий влияние на условия работы арматурных элементов наличия сварных стыков (с зачисткой)(приr=r_b=0.101);

e_rs - коэффициент, зависящий от коэффициента асимметрии цикла r:

    Следовательно e_rs =0.7;

m_as1 = 1·0.7=0,7.

 

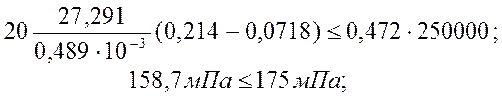Условие выполняется.

2.1.9 Расчёт нормального сечения плиты на трещиностойкость.

При расчете на трещиностойкость проверяем выполнение условий по образованию продольных трещин и по раскрытию нормальных трещин:

а) расчет на трещиностойкость по образованию продольных трещин сводится к ограничению нормальных напряжений в бетоне:

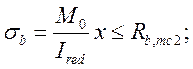                                     (2.33)

где  - расчётное сопротивление  бетона класса В22,5 осевому сжатию на стадии эксплуатации [2, п.3.24];

М₀=21.204кН·м – изгибающий момент для расчета на трещиностойкость;

Ired – момент инерции приведенного сечения плиты относительно нейтральной оси без учета растянутой зоны бетона и с учетом приведенной площади арматуры (см. формулу (2.27);

 x - высота сжатой зоны бетона, принятая из расчета по прочности.

 

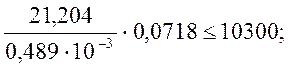Условие выполняется.

б) расчет на трещиностойкость по раскрытию нормальных трещин выполняем из условия:

 

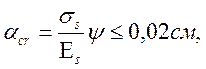(2.34)

где = 2,06·10⁵мПа ([2]п.3.47);

= М₀ /(А_s(h₀ – 0,5x)) – напряжение в арматуре;

Ψ – коэффициент раскрытия трещин: при арматуре периодического профиля Ψ = 1,5 √¯R_r,

где Rr = A_r/(βnd); здесь β = 1 – коэффициент учитывающий степень сцепления арматурных элементов с бетоном ([2],п.3.110); n – количество стержней рабочей арматуры на ширине плиты b = 100см; d – диаметр стержней арматуры, см;

A_r=b(6d + a_s) – площадь взаимодействия бетона и арматуры, см2, ограниченная контурами сечения по верхней грани и прямой, отложенной на расстоянии шести диаметров от оси арматурных стержней (a_s – расстояние от оси арматурных стержней до растянутой грани плиты).

A_r=100(6·1.2 + 2.6)=980см²;

Rr = 980/1·8·1,2=102,083см;

Ψ = 1,5 √¯102,083=15,155;

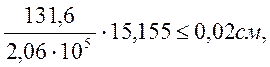
= 21,204·10³ /(9,048·10^-4·(0,214 – 0,5·0,0718))=131,6мПа

 

Условие выполняется.

В результате проведённых проверок принимаем 8 стержней арматуры класса AII и диаметром 12 мм.

2.2 Расчёт главной балки.