2.2.1 Определение нормативных постоянных нагрузок.
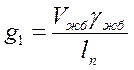 В отличие от нагрузок, принимаемых
для расчета плиты балластного корыта, в данном расчете примем нагрузку от
собственного веса конструкций пролетного строения, приходящуюся на 1 м длины двух балок, кН/м:
В отличие от нагрузок, принимаемых
для расчета плиты балластного корыта, в данном расчете примем нагрузку от
собственного веса конструкций пролетного строения, приходящуюся на 1 м длины двух балок, кН/м:
(2.35)
где Vжб – объем железобетонного пролетного([1] прил.В).
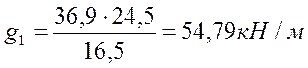 |
Другие постоянные нагрузки - g2 – вес двух тротуаров с перилами, равный 9,8 кН/м; g3=4.18·0.5·19.6=40.96кН/м - вес балласта с частями пути.
2.2.2 Построение
линий влияния изгибающих моментов и поперечных сил. Определение нормативных
временных вертикальных нагрузок. Нормативную временную вертикальную
нагрузку принимаем в соответствии с длинами загружений линий влияния (см.
Рис.2.3) и данными [1] прил.Н при ![]() = 0,5 независимо
от положения вершины линии влияния, т.к. путь устроен на балласте:
= 0,5 независимо
от положения вершины линии влияния, т.к. путь устроен на балласте:
![]()
![]()
![]()
Вычислим необходимые для дальнейших расчетов площади линий влияния:
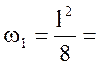 31,205 м2;
31,205 м2;
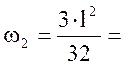 23,404 м2;
23,404 м2;
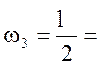 7,9 м2;
7,9 м2;
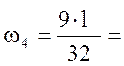 4,44 м2;
4,44 м2;
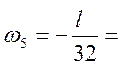 -0,49 м2;
-0,49 м2;
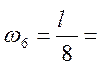 1,975 м2
1,975 м2
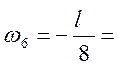 -1,975 м2
-1,975 м2
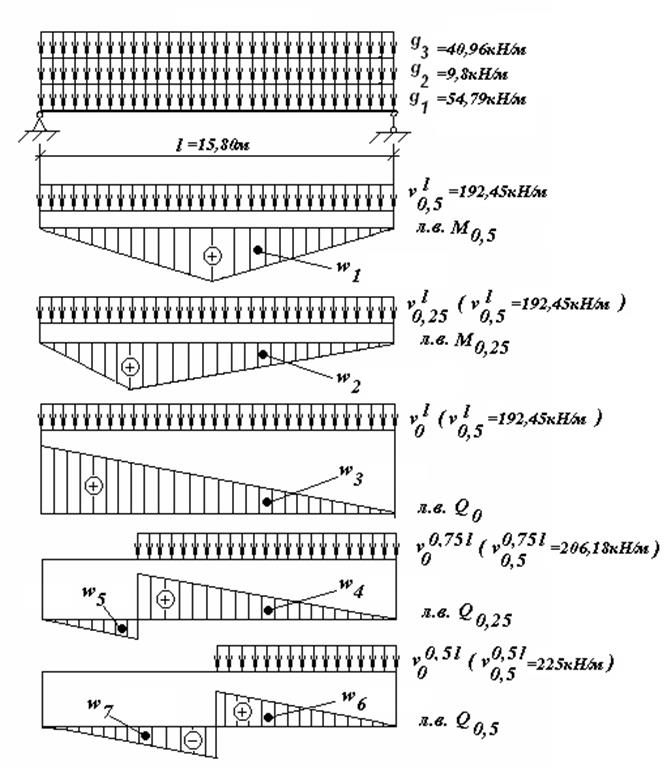
Рис. 2.3 Линии влияния.
2.2.3 Определение расчетных внутренних усилий для расчетов на прочность, выносливость и трещиностойкость.
Определим коэффициенты для нагрузок, которые понадобятся для дальнейших расчётов:
·
![]() f - коэффициенты
надежности по нагрузкам ([1] прил.П), для постоянных нагрузок:
f - коэффициенты
надежности по нагрузкам ([1] прил.П), для постоянных нагрузок: ![]() fg1=
fg1=![]() fg2=1,1,
fg2=1,1,
![]() fg3=1,3, для временных нагрузок:
fg3=1,3, для временных нагрузок: ![]() fvλ=15.8=1.253,
fvλ=15.8=1.253, ![]() fvλ=7,9=1,276,
fvλ=7,9=1,276, ![]() fvλ=11,85=1,264.
fvλ=11,85=1,264.
· ε – коэффициент, учитывающий влияние транспортеров ([1] прил.П), для λ=15,8 и λ=11,85 ε=0,85, для λ=7,9 ε=0,91.
· (1+μ) и (1+2/3μ) – динамические коэффициенты для расчета соответственно по прочности и выносливости ([1] прил.П).
Λ=15,8 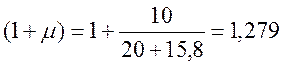
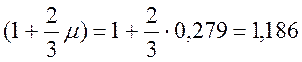
Λ=11,85 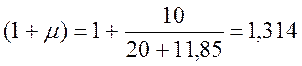
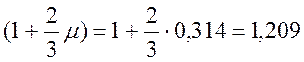
Λ=7,9 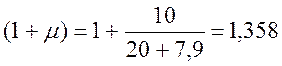
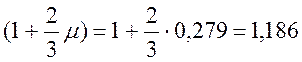
Определим расчетные усилия:
· для расчётов по прочности:
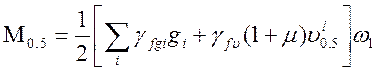 |
(2.36)
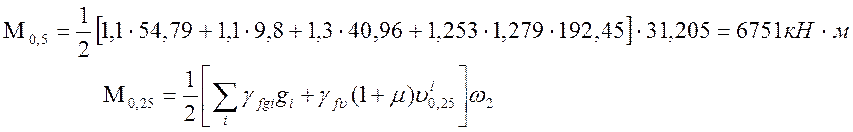 |
(2.37)
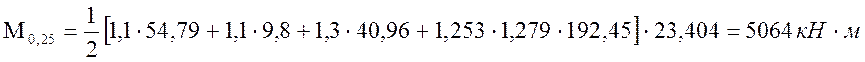
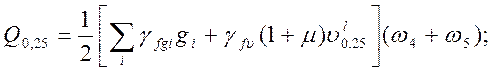 |
(2.38)
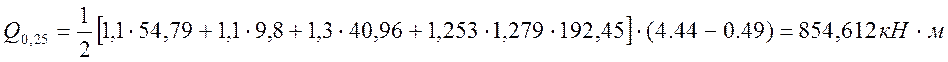 |
|||
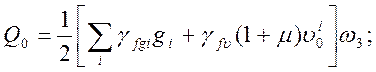 |
|||
(2.39)
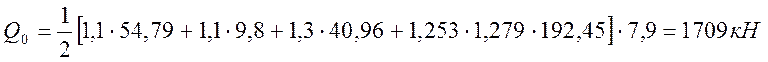 |
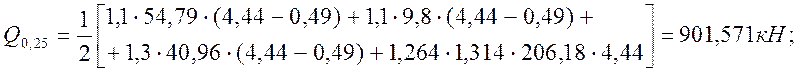
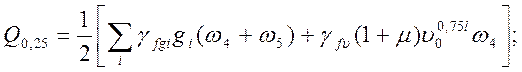 (2.40)
(2.40)
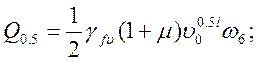 |
(2.41)
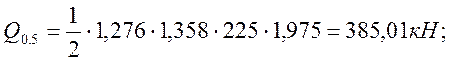
· для расчётов на выносливость:
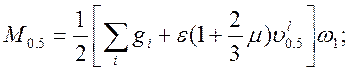 |
(2.42)
(2.43)
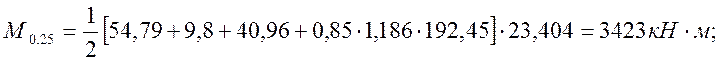 |
· для расчётов по трещиностойкости:
по образованию продольных трещин:
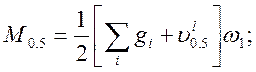 |
(2.44)
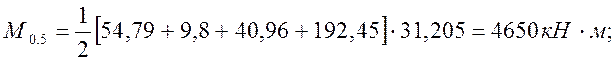 |
по раскрытию нормальных трещин:
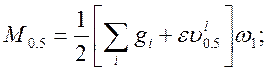 |
(2.45)
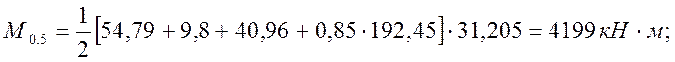 |
по ограничению касательных напряжений:
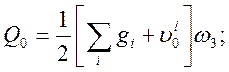 |
(2.46)
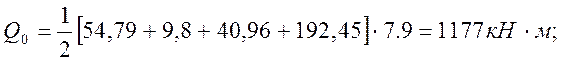 |
по раскрытию наклонных трещин:
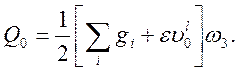 |
(2.47)
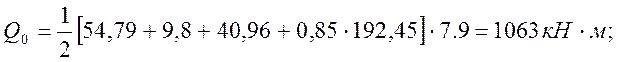 |
2.2.4 Назначение расчётного сечения балки и подбор рабочей арматуры в середине пролёта.
Основные размеры сечения главной балки заданы преподавателем (см. П.2.1.1) и дополнены, исходя из принятых на практике и рекомендуемых в литературе данных ([1] прил.В). Сечение главной балки чаще принимаем тавровым. Расстояние между осями балок принимаем равным 1800 мм. Для расчета в курсовом проекте фактическое поперечное сечение пролетного строения заменяем на сечение упрощенной формы (см. рис. 2.4).
Приведенная толщина плиты может быть определена по формуле:
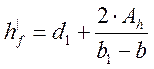
(2.48)
где Аh –площадь вутов, Ah=(0.62-π·0.32)/4=0,019м2 (см.рис.2.4).
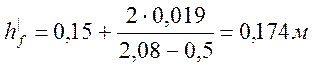 |
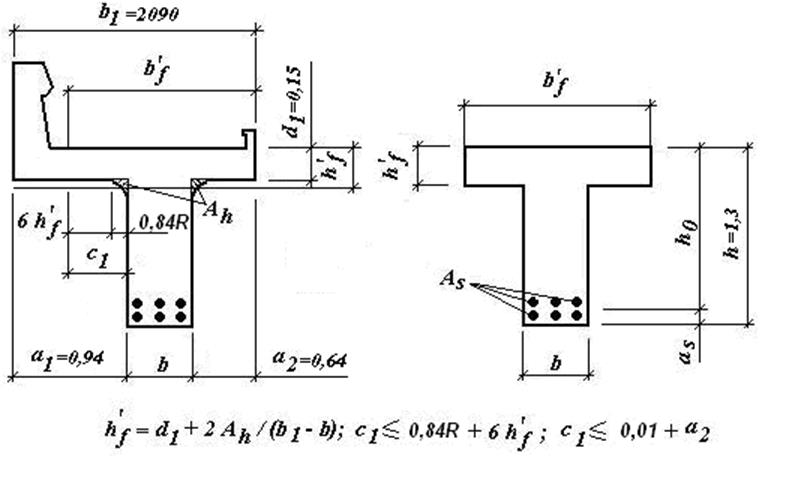
Рис. 2.4 Расчётные размеры главной балки.
Далее зададимся рабочей высотой сечения h0 = 0,85h = 1,105м.
Определим длину свесов: c1≤0.9R+6h’f; c2≤0.9R+a2;
с1≤ 1,314; с2≤0,91.
Примем длину свеса С=0,91м.
Зададимся рабочей высотой сечения: h0=0.85·h=1.3·0.85=1.105м.
В первом приближении определяем требуемую площадь рабочей (растянутой) арматуры из условия:
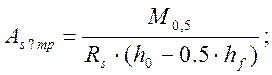 |
(2.49)
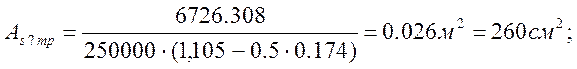 |
Зададимся диаметром арматуры: d=36, тогда А1=10.180см2.
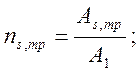 Требуемое количество стержней в нижнем поясе балки
определим по формуле:
Требуемое количество стержней в нижнем поясе балки
определим по формуле:
(2.50)
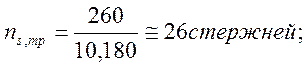 |
Фактическое значение площади всей арматуры в растянутой зоне будет равно: Аs,ф=А1 · ns=26·10.108=262.808см2.
Составляем схему размещения арматурных стержней в нижнем поясе балки (см.рис.2.5). Арматурные стержни располагаем симметрично относительно вертикальной оси балки.
Назначаем толщину защитного слоя бетона: Сб=3см. В вертикальных рядах арматуру размещаем пучками по 2 стержня без просветов. Между пучками устраиваем просветы, равные 5 см при двух стержнях в группе. Расстояние в свету между вертикальными рядами арматуры Сп=6,5см (при расположении арматуры в три ряда).
Затем вычисляем расстояние от центра тяжести сечения растянутой арматуры до нижней грани балки:
as = ∑niai / ns, (2.50)
где ni – количество стержней в i – м ряду; ai – расстояние от оси i – го ряда до нижней грани балки.
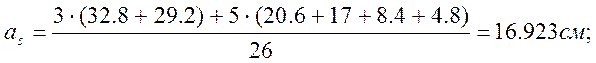 |
После этого уточняем рабочую высоту сечения h0 = h – as=1,3-0,16923=1,131м.
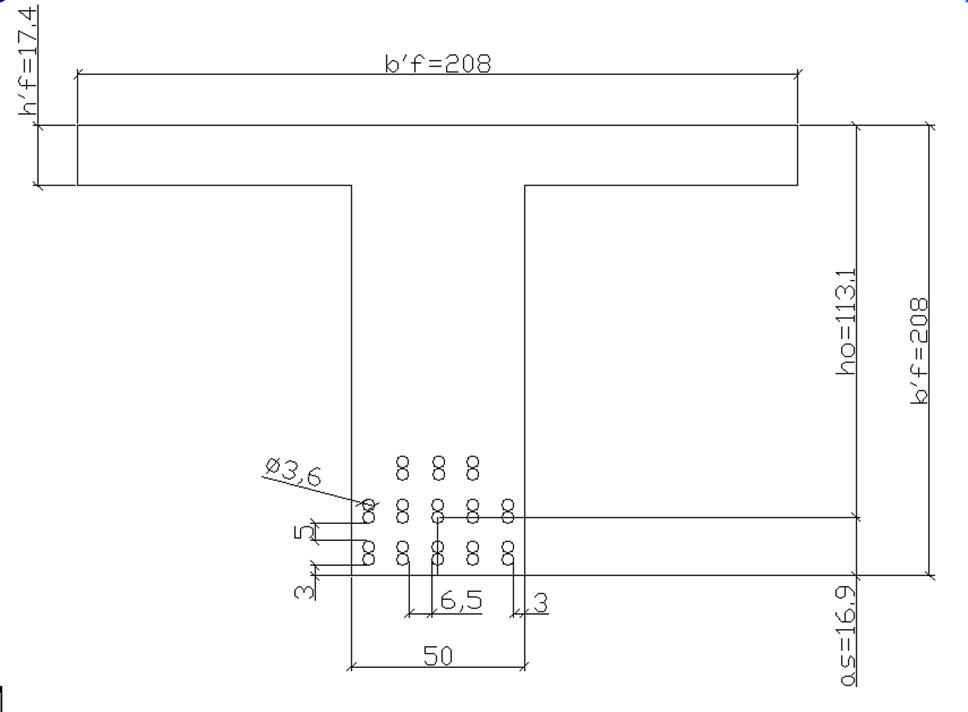
Рис. 2.5 Схема расположения стержней арматуры в нижнем поясе балки.
2.2.5 Расчет балки на прочность нормального сечения в середине пролета.
Проверим следующее условие:
(2.51)![]()
Условие не выполняется, значит нейтральная ось проходит в пределах ребра главной балки (рис. 2.6) и сжатая зона сечения балки имеет тавровую форму. Высоту сжатой зоны определим по формуле:
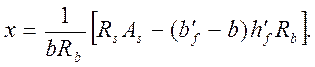 |
(2.52)
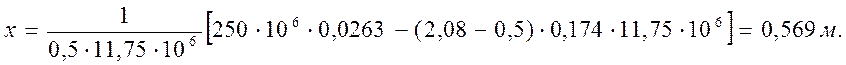
Проверим условие:x = х/h0 ≤ xy = (0,85 – 0,008 Rb) / (1 + 0,0001Rs(4,545 – 0,145Rb)). Здесь Rb и Rs принимаем в МПа.
xy = (0,85 – 0,008·11,75) / (1 + 0,0001·250·(4,545 – 0,145·11,75))=0,706;
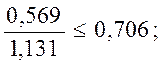 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.