Проектирование железобетонного моста под железную дорогу через постоянный водоток в Новосибирской области, страница 7

Условие выполняется.

Далее проверим прочность нормального сечения по следующей формуле:

 

(2.53)

 

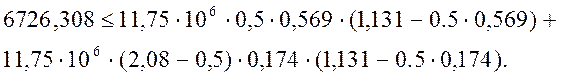Условие не выполняется.

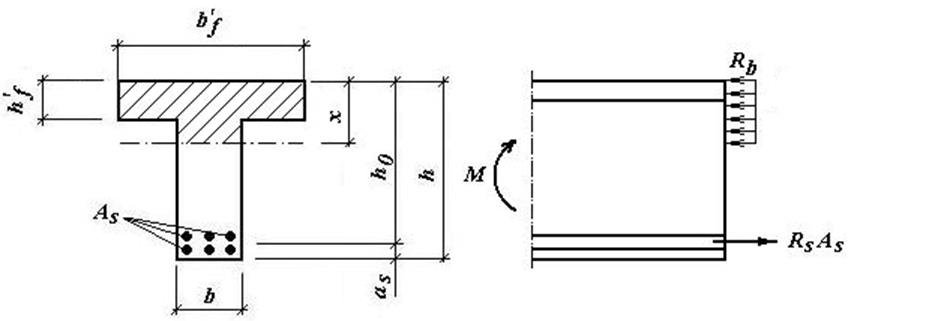
Рис. 2.6 Схема к расчёту нормального сечения в середине пролёта.

2.2.6 Расчет балки на выносливость нормального сечения в середине пролета.

В расчетах на выносливость принимаем, что растянутый бетон полностью выключился из работы сечения и все растягивающее усилие воспринимается арматурой (см. Рис. 2.7). В этом случае наибольшие напряжения в бетоне и арматуре балки определим по формулам:

 

                                           (2.54)                                                                                                                          

где M_f,max – изгибающий момент для расчетов на выносливость (см. формулу (4.24));

h_u – расстояние от крайнего ряда растянутой арматуры до сжатой грани (h_u=0,99).

В результате расчета на выносливость выясним выполнимость двух условий: 

                                                                           

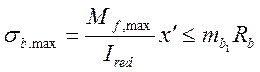
(2.55)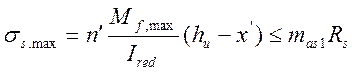

где - высота сжатой зоны;

I_red - приведенный момент инерции;

- отношение  модуля упругости арматуры к модулю упругости бетона (для бетона В22.5 n’=20).

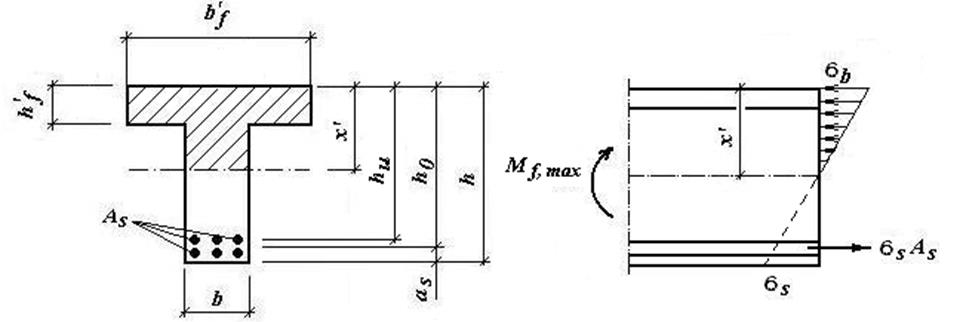
Рис. 2.7 Схема к расчёту балки на выносливость.

Для определения расчётных сопротивлений бетона и арматуры вычислим характеристики цикла повторяющихся напряжений по формуле: ρ_b = ρ_s = M_f,min / M_f,max, (причём значения M_f,minи  M_f,max определим по формуле 2.42). ρ_b = ρ_s =1619,161/4648,633=0,348, значит ε_b=1,124, ε_ps=0,829 ([1] прил.М).

m_b1 = 0,6·1,34·1,124=0,904 (см. формулу 2.29);

m_as1 = 1·0,829=0,829 (см. формулу 2.32).

Высота сжатой зоны х’:

(2.56)

где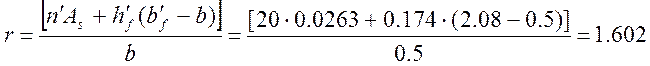

 

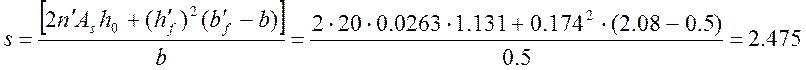
Приведённый момент инерции:

(2.57)

 

а) выносливость по бетону:

 

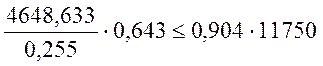Условие не выполняется.

б) выносливость по арматуре:

 

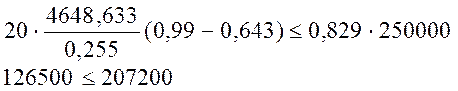  Условие выполняется.

2.2.7 Расчет балки на трещиностойкость нормального сечения в середине пролета.

  Расчёт по образованию продольных трещин:

 

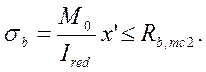(2.58)

  где М₀ – момент от нормативных постоянных и временных нагрузок в середине пролёта.

  R_b,mc2=10300 кПа  -  расчётное сопротивление  бетона класса В22,5 осевому сжатию на стадии эксплуатации [2, п.3.24].

 

 

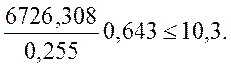  Условие не выполняется.

  Расчёт по раскрытия трещин:

 

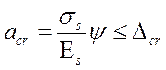(2.59)

  где σ_s=;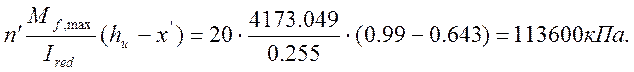

  E_s=2,06·10⁶мПа - модуль упругости арматуры класса АII ([1] прил.М);

  Ψ – коэффициент раскрытия трещин: при арматуре периодического профиля Ψ=8,886 (см.2.1.9)т.к. A_r=b(h-x’)=50(130-64.3)=3285см², R=A_r/bnd=3285/1·26·3.6=35,096см.

  - предельное значение расчетной ширины раскрытия трещин принимается не более 0,020 см (табл. 39* [2]).

 

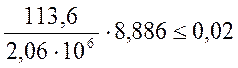Условие выполняется.

  По итогам проверок можно сделать вывод, что необходимо увеличение количества стержней арматуры или увеличение их диаметра. Но данные действия не привели к нужному результату – по итогам исследования нескольких расчетных схем, принято решение о:

1. Повышении класса бетона до В25

2. Увеличении количества стержней до 30.

3. Принята расчетная схема, изображённая на рис.2.8.

  Расчет произведён на ЭВМ, результаты расчёта данной расчётной схемы приведены в приложении.

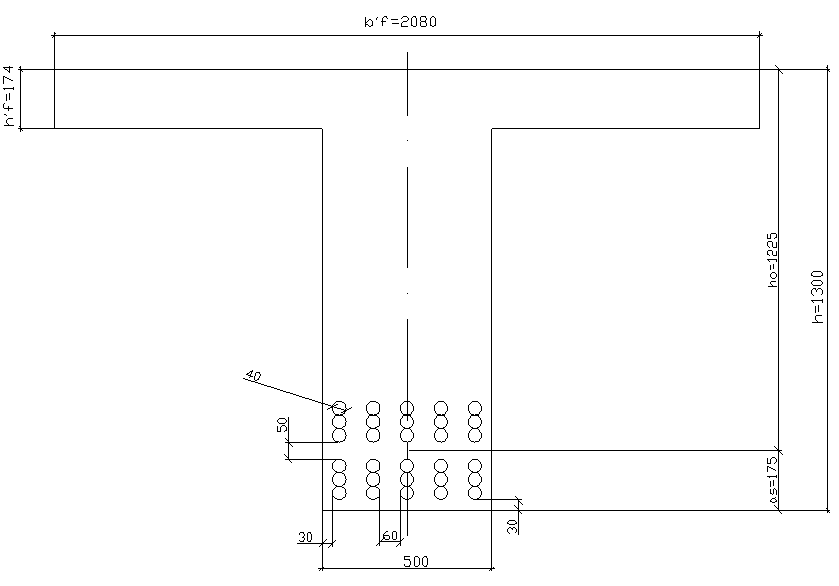
Рис. 2.5 Схема расположения стержней арматуры в нижнем поясе балки (исправленная).

2.2.8 Построение эпюры материалов с определением мест отгибов рабочей арматуры.

  Для определения мест отгибов рабочей арматуры строим огибающую эпюру максимальных моментов в балке.

  Начало отгибов продольных растянутых стержней арматуры располагаем за сечением, в котором стержни учитываются с полным расчётным сопротивлением. Длину заводки за сечение для арматуры стали класса АII и бетона класса В25 определяем по формуле:

 

(2.60)

 

  Построение эпюры материалов, а также определение мест отгибов рабочей арматуры ведём в соответствии с требованиями [2]:

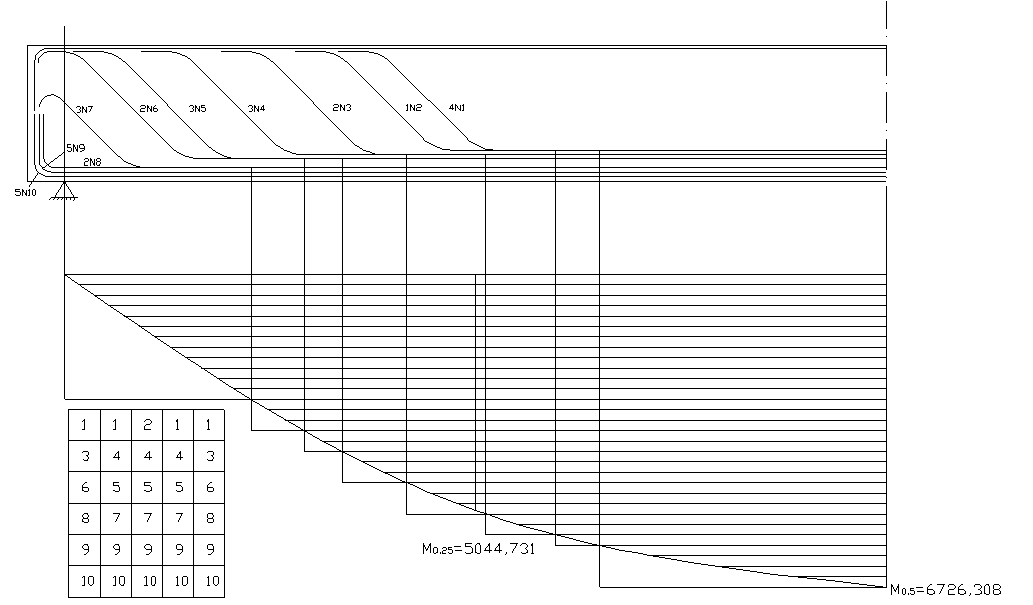
Рис. 2.6 Схема для расстановки наклонных стержней.

2.2.9 Расчёт на прочность наклонных сечений главной балки.

  1. Расчёт на прочность по сжатому бетону между наклонными трещинами:

                                             (2.61)

  где  Q - поперечная сила на расстоянии не ближе h₀ от оси опоры, Q=1493,183кН;

 = 1 + ηn₁A_sw/(bS_w), при расположении хомутов нормально к продольной оси  ≤1,3;

  η =5 – при хомутах, нормальных к оси элемента;

  n₁ – отношение модулей упругости арматуры и бетона (п. 3.48 [2]), n₁=20;

  A_sw – площадь сечения ветвей хомутов, расположенных в одной плоскости A_sw=2·3,14·0,01²/4=1.57·10^{-4 м2};

  S_w – расстояние между хомутами по нормали к ним, S_w=0.15м;

  - толщина стенки (ребра) главной балки;

  = 1 – 0,01R_b – коэффициент. Здесь R_b принимаем  в МПа, =1-0,01·13=0,87;

   - рабочая высота сечения, =1,125м.

 = 1 +5·20·0,000157/(0,5·0,15)=1.209

 

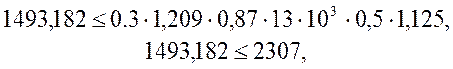  Условие выполняется.

  2. Расчёт наклонного сечения на действие поперечной силы:

                   (2.62)

  где  - максимальное значение поперечной силы от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения;  и  - суммы проекций усилий всей пересекаемой арматуры при длине проекции сечения (см. рис 2.7);- расчетное сопротивление арматуры с учетом коэффициента m_a4:

;                        (2.63)

МПа;

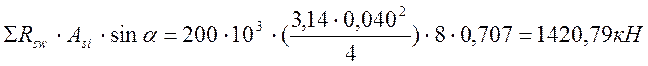  кН;

  ;

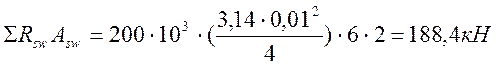 - поперечное усилие, передаваемое в расчете на бетон сжатой зоны над концом наклонного сечения и определяемое по формуле:

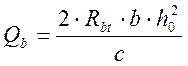  ;                     (2.64)

;

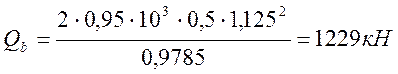  1702,863 < 1420,79+188,4+1229;

  1702,863 кН < 2838 кН.

  Условие на действие поперечной силы выполняется.

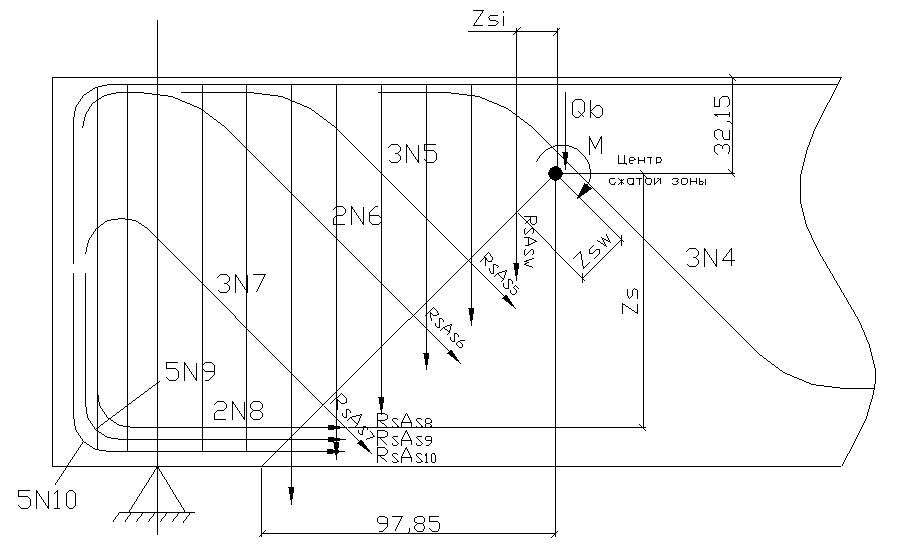
Рис. 2.7 Схема для расчёта наклонного сечения.

3. Расчет наклонного сечения на действие изгибающего момента.