ТЕМА: Теорема Піфагора
Перпендикуляр і похила
МЕТА: систематизувати знання , уміння і навички учнів щодо вивченої теореми. Вчити застосовувати згадану теорему та наслідки з неї до розв’язування задач. Розвивати логічне мислення, увагу, пам’ять, спостережливість. Виховувати культуру математичного запису і мовлення.
ПЛАН: 1) Перевірка домашньої роботи.
2) Цікаві відомості з історії.
3) Математичний диктант.
4) Розв’язування задач за малюнками.
5) Розв’язування текстових задач.
6) Повідомлення про важливість теореми Піфагора.
7) Підсумок уроку; домашнє завдання.
ХІД УРОКУ:
1. Перевірка домашньої роботи.
№141.
1) ![]() –
катет,
–
катет, ![]() см
см
2) ![]() –
гіпотенуза,
–
гіпотенуза, ![]() см.
см.
№144.
Дано: ![]() –
прямокутний;
–
прямокутний;
![]() см;
см;
![]()
Знайти: ![]() ;
; ![]() ;
; ![]() .
.
Розв’язання.
Нехай ![]() см – коефіцієнт пропорційності, тоді
см – коефіцієнт пропорційності, тоді ![]() (см), а
(см), а ![]() (см).
Так як периметр 80 см, то
(см).
Так як периметр 80 см, то ![]() (см). За теоремою
Піфагора маємо рівняння
(см). За теоремою
Піфагора маємо рівняння
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
 ;
;
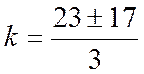 ;
;
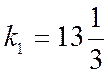 ;
; ![]() ,
,
1) 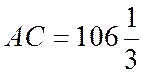 см;
см; ![]() см; – не задов.
см; – не задов.
2) ![]() см;
см; ![]() см;
см; ![]() см.
см.
Відповідь: 34 см; 16 см; 30 см.
№145.
Дано: ![]() (
(![]() =90º);
=90º);
![]() см;
см;
![]() см;
см;
Знайти: ![]() ;
; ![]() ;
; ![]() .
.
Розв’язування. ![]() см;
см; ![]() см;
см;
![]()
![]() ;
;
![]() ;
;
![]()
![]() см;
см;
![]() см;
см;
![]() см.
см.
Відповідь: 10 см; 8 см; 6 см.
№166.
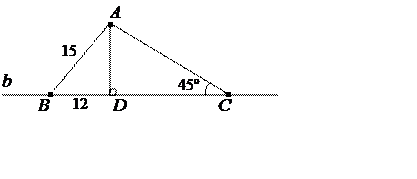 Дано:
Дано: ![]() ;
; ![]() – похилі
– похилі
![]() –
проекція
–
проекція ![]() на
на ![]()
![]() см;
см;
![]() см
см
![]() 45º.
45º.
Знайти: ![]() .
.
Розв’язання.
![]() (см)
(см)
![]() –
рівнобедрений прямокутний, тому
–
рівнобедрений прямокутний, тому ![]() см.
см.
За теоремою Піфагора
![]() ;
;
![]() (см)
(см)
Відповідь: ![]() см.
см.
2. Цікаві відомості з історії
1) Піфагор Самоський;
2) Піфагор та його теорема;
3) Єгипетський трикутник.
3. Математичний диктант.
|
1 |
І в |
Косинус гострого кута не залежить від … |
1 б |
|
ІІ в |
Косинус гострого кута прямокутного трикутника це … |
||
|
2 |
І в |
В Єгипетському трикутнику гіпотенуза пропорційна числу … |
1 б |
|
ІІ в |
В Єгипетському трикутнику катети пропорційні числам … |
||
|
3 |
І в |
Чи правда, що в прямокутному трикутнику відношення прилеглого до гострого кута катета до гіпотенузи більше від одиниці ? |
1 б |
|
ІІ в |
Чи правда, що в прямокутному трикутнику відношення прилеглого катета до гіпотенузи дорівнює одиниці? |
||
|
4 |
І в |
Для трикутника |
1 б |
|
ІІ в |
Для трикутника |
||
|
5 |
І в |
Чи правда, що похила більша за перпендикуляр? |
1 б |
|
ІІ в |
Чи правда, що проекція похилої на пряму більша за саму похилу? |
||
|
6 |
І – ІІ в |
Якщо катети прямокутного трикутника 6 см; 8 см [12 см; 9 см], то його гіпотенуза дорівнює … |
2 б |
|
7 |
І – ІІ в |
З однієї точки до прямої проведено дві рівні похилі. Проекції цих похилих дорівнюють по 5 см. Знайдіть відстань між основами похилих [Відстань між їх основами 16 см. Знайдіть довжини проекцій цих похилих на дану пряму]. |
2 б |
|
8 |
І – ІІ в |
Якщо довжина похилої, проведеної з даної точки до прямої становить 25 см, а довжина її проекції на пряму 15 см [20 см], то відстань від точки до прямої становить … |
2 б |
|
9 |
І в |
Якщо у прямокутному трикутнику гострий кут становить 45º, то такий трикутник … |
1 б |
|
ІІ в |
Яка властивість у прямокутного трикутника з гострим кутом 30º? |
4. Розв’язування задач з малюнками.
Знайти ![]() .
.
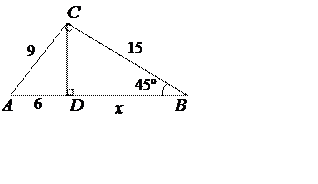
 1) 2)
1) 2)

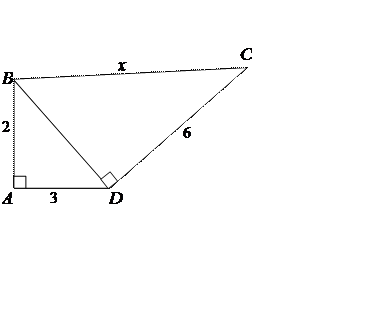 3) 4)
3) 4)
5. Розв’язування текстових задач.
Завдання біля дошки (виконується під час написання математичного диктанту).
1) Знайти периметр прямокутника, одна із сторін якого дорівнює 10 см, а діагональ – 26 см.
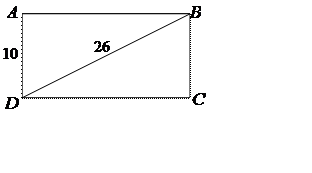
![]() (см),
(см),
![]() (см).
(см).
2) Основи рівнобічної трапеції дорівнюють 7 см і 19 см, а бічна сторона 10 см. Знайти висоту трапеції.
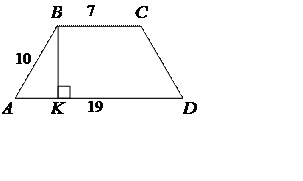
![]() (см),
(см),
![]() (см).
(см).
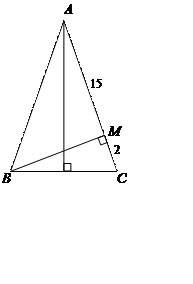 3) Висота
3) Висота ![]() рівнобедреного трикутника
рівнобедреного трикутника ![]() (
(![]() )
ділить сторону
)
ділить сторону ![]() на відрізки
на відрізки ![]() см і
см і ![]() см.
Знайти основу
см.
Знайти основу ![]() трикутника.
трикутника.
![]() (см),
(см),
![]() (см).
(см).
4) З точки до прямої проведено дві похилі, проекції яких на пряму дорівнюють 9 см і 16 см. Знайти відстань від точки до прямої, якщо одна з похилих на 5 см більша за другу.

![]() ;
;
![]() см;
см; ![]() см;
см;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() (см).
(см).
Відповідь: 12см.
6. Важливість теореми Піфагора.
7. Підсумок уроку.
Домашнє завдання: §7, п. 62-66 – повн. с. 116, К–3; В–2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.