Теорема Піфагора: План-конспект уроку геометрії

Міністерство освіти і науки України

Полтавский державний педагогічний університет ім. В.Г. Короленка

Кафедра математичного аналізу

та інформатики

План - конспект уроку геометрії

Тема: теорема Піфагора.

Виконав

студент групи МІ-53

фізико-математичного факультету

Феленко Сергій Васильович

Полтава-2004

ПЛАН-КОНСПЕКТ УРОКУ ГЕОМЕТРІЇ В 8 КЛАСІ

Тема: теорема Піфагора.

Мета:познайомити учнів зі змістом і доведенням теореми    Піфагора. Показати її застосування при розе 'язуванні задач;

- сформувати вміння розв’язувати найпростіші завдання;

- виховати працьовитість та охайність.

Обладнання: дошка, крейда , підручник.

Тип уроку: урок засвоєння нових знань.

План проведення уроку:

I.       Організаційний момент .

ІІ.     Перевірка домашнього завдання .

ІІІ.    Вивчення нового матеріалу .

ІV.    Закріплення нових знань і вмінь учнів .

V.  Підсумок уроку і завдання додому

Хід уроку.

І.     Організаційний момент:

- перевірка відсутніх;

- оголошення теми і завдання уроку

Хід уроку

ІІ.    Перевірка домашнього завдання

Питання до класу

·  Що називають косинусом гострого кута прямокутного трикутника?

·  Малюнку 1, а — в  вкажіть прямокутні трикутники, котрим належать позначені гострі кути; запишіть косинуси позначених кутів, виразившії їх через відношення сторін трикутників. (Малюнки заздалегідь заготов­лені на дошці.)

Мал.1

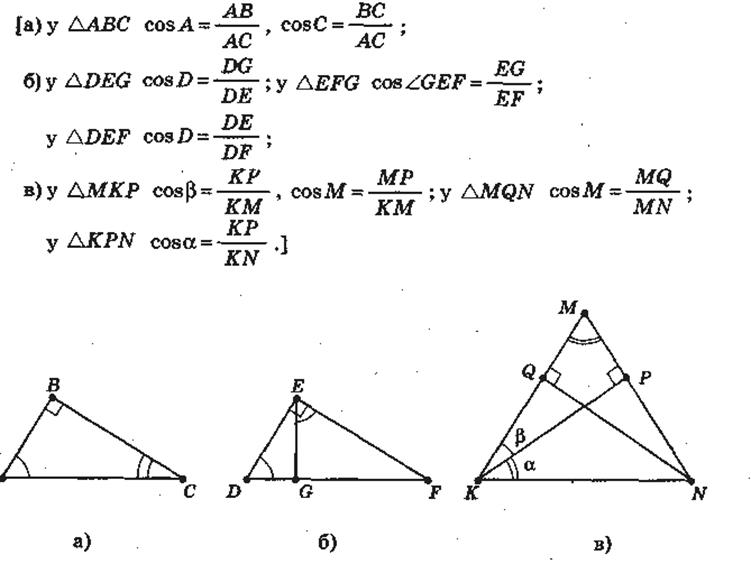
·  Чи залежить косинус кута трикутника від розмірів і розміщен­ня трикутника? Відповідь обґрунтувати. [Ні, тому що зі зміною розмірів чи розташування трикутника косинус його гострого кута не змінюється.]

·  Від чого залежить косинус кута трикутника? [Від градусної міри кута.]

ІІІ. Вивчення нового матеріалу

Теорема Піфагора

Матеріал п. 63 підручника доцільно розподілити на три уроки: на периому розглянути теорему Піфагора, другий урок присвятити розв'язанню задач, а третій — наслідкам з теореми Піфагора.

Пояснення нового матеріалу можна почати зі створення проблемної ситуації.        

Завдання класу

•  Знайдіть довжину приставленої до будинку драбини, якщо нижній її кінець знаходиться на відстані 3 м від будинку, а верхній — на стику стіни й даху. Висота стіни будинку дорівнює 4 м.

 Потім задача формулюється в загальному вигляді.

•  Знайдіть довжину гіпотенузи прямокутного трикутника за його катетами.
Учитель зауважує, що учні не можуть розв'язати цю задачу, тому що не знають формули, яка виражає зв'язок між сторонами цього трикутника.

Формулюється теорема Піфагора.

          У прямокутному трикутнику квадрат гіпотинузи дорівнює сумі квадратів катетів.

На дошці й у зошитах учні виконують малюнок і записують умову й до­ведення теореми.

Теорема

Дано: у ∆АВС C = 90°, AC = b, BC = a, AB = c.

Д о в е с т и: с²=а² + Ь².

Зауваження. Оформлення доведення теореми бажано зробити більш детальним,  ніж те, яке дається в підручнику. Воно може бути таким, як показано нижче. Для  зручності запису доцільно використовувати позначення: aib — катети,  с — гіпо­тенуза, а_с і Ь_с —відрізки гіпотенузи BD і AD, якщо CD _┴ AB; A і B —гострі кути і C = 90°.

Доведення

Проведемо додаткову побудову (д. п.): CDAB, DAB (Мал.2).

 Позначимо AD через b_с, a BD — через а_с.

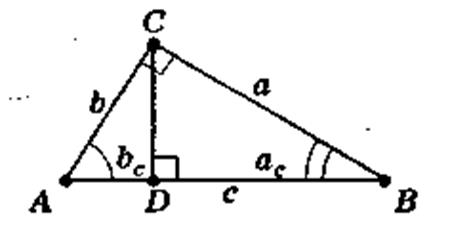
Мал.2

За означенням косинуса кута маємо:

1) з ∆ACD  cosA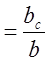, з ∆АВС   cosA.

 Отже, 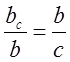, тобто ;

2) з ∆ВСD   cosB 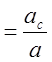, з ∆АВС   cosB.

Отже, 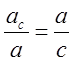, тобто ;

3) тоді a²+b²=ca_c+cb_c=c(a_c+b_e) = c-c = c².

с²= а² + Ь² — квадрат гіпотенузи дорівнює сумі квадратів катетів.

ІV. Закріплення нових знань і вмінь учнів

Задача 1 (про драбину).

Дано: у ∆АВС  С = 90°, АС = 3 м, ВС = 4 м.

З н а й т и: АВ.

Роз в'я з а н н я

АВ — гіпотенуза ∆АВС . Отже, за теоремою Піфагора                         АВ² = АС² + ВС² = З² +4² =9+16 = 25.

АВ = = 5 (м).

Відповідь: 5м.                                             

Задача 2.

Дано: у ∆АВС C = 90°, AC = BC = 3м.

З н а й т и: АВ.

Роз в'я з а н н я

АВ — гіпотенуза ∆АВС,отже, АВ² = АС² + ВС² (за теоремою Піфагора).

АВ²=3²+3²=92, АВ = =3(м).

Відповідь.   3м .

Задача 3.

Дано: у ∆АВС  C = 90°, гіпотенуза c=25дм,  а катет a = 20дм .

Знайти: катет b.

Роз в'я з а н н я

[За теоремою Піфагора с² = а² + b²; 25² = 20² +b²,    

b² = 25² - 20² =  (25 + 20)(25-20) = 45 5 = 925;

 b = 35 = 15(дм).]

Відповідь:  15дм.

Задача 4.

Дано: у прямокутному трикутнику задані гіпотенуза

с = 4см  і катет b = 3см.

Знайти: катет а.

Роз в'я з а н н я

За теоремою Піфагора c²=а²+b², 16 = а²+9, а²=16-9 = 7, а =(см).

Відповідь.см.

V. Завдання додому

Питання 3 § 7. Задачі № 2 (3), 3 (3) § 7.

Задача 2(3).

Дано: у ∆АВС  С = 90°, АС = 11 м, ВС = 60 м.

З н а й т и: АВ.

Роз в'я з а н н я

АВ — гіпотенуза ∆АВС . Отже, за теоремою Піфагора                      АВ² = АС² + ВС² = 11² +60² =121+3600 = 3721.

АВ = = 61 (м).

Відповідь: 61м.

Задача 3(3).

Дано: у прямокутному трикутнику задані гіпотенуза

с = 25см  і катет b = 7см.

Знайти: катет а.

Роз в'я з а н н я

За теоремою Піфагора c²=а²+b², 625 = а²+49, а²=625-49 = 576,                           а ==24(см).

Відповідь:24см.