Министерство науки и образования Украины
Полтавський государственный педагогический университет
им. В. Г. Короленка
кафедра математики
План – конспект урока на тему:
«Уравнение окружности»
разработал студент
физико-математического
факультета
группы М-42
Чиж Юрий
Александрович
Полтава 2005
Тема: Уравнение окружности
Цель:
Ø обучающая: закрепить знания по даной теме, а в частности координаты середины отрезка, расстояние между точками, уравнение окружности, и также научить учеников решать типичные задачи;
Ø развивающая: развивать теоретическое, абстрактное и логическое мышление, разширение научного мировозрения;
Ø воситательная: воспитывать у детей дисциплинированость, старательность, чистоту и правильность записи, любовь к математике.
Тип урока: комбнированный.
Оборудование: линейка, циркуль, доска и учебники.
План урока:
1. Организационный момент 2 мин.
2. Актуализация знаний 5мин.
3. Решение задач 35 мин.
4. Подведение итогов урока и домашнее задание. 3 мин.
Ход урока:
1.Организационный момент.
Учитель входит в класс, здоровается с детьми, упокаивает их после бурной перемены и настраивает на работу в течении всего урока.
2. Актуализация знаний.
Один ученик у доски выводит уравнение окружности с центром в точке А ( а; b) и радиусом R.
На доске записаны уравнения окружностей и по желанию учителя ученики с места называют центр и радиус. А затем наоборот.
Найдите центр и радиус окружности.
1) (x - 2)2 + ( y + 3)2 = 9;
2) (x - 6)2 + y2 = 4;
3) x 2 + (y + 7)2 =25;
4) (x + 5)2 + (y - 2)2 = 36;
5) x2 + y2 = 16;
6) (x - 7)2 + (y + 1)2 = 10;
Составте уравнение окружности с центром и радиусом:
1) О (3; 6), R = 3
2) О (-2; -4), R = 5
3) О (-0,5; 0,6), R = 13
3. Решение задач.
№ 24
Дано точки А (-1; 2) и В (-5; 4). Составте уравнение окружности с центром в точке В и которая проходит через точку А.
Решение:
![]()
![]()
№ 25
Точки А (3; -4) и В (1; 2) – концы диаметра окружности. Найдите: 1) центр окружности; 2) радиус окружности; 3) уравнение окружности.
Решение:
О (x; y)
– центр окружности; 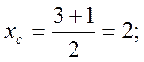
![]()
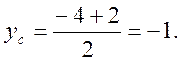
1) О (2; -1) – центр;
2) ![]()
3) ![]()
№ 27
Составьте уравнение окружности, которая прикасается к оси абсцисс и прямых x = -1 и x = 5.
Решение:
2R = |-1 - 5| = |-6| = 6; тогда R = 3.
О (2;
3) – центр окружности, тогда можем записать уравнение окружности: ![]()
№ 29
Дана окружность x2 + y2 = 25 и две точки А (3; 4) и В (4; -3). Докажите, что АВ – хорда данной окружности.
Решение:
Для начала, проверим, принадлежат ли эти точки окружности:
А (3; 4): 32 + 42 =25
25 = 25,
В (4; -3): 42 + (-3)2 = 25
25 = 25.
Обе эти точки принадлежат этой окружности. Радиус окружности можно увидеть из уравнения, он равен 5.
![]()
АВ меньше диаметра, значит это хорда.
№ 13*
Найти центр и радиус окружностей.
а) ![]()
б) ![]()
Решение:
а) ![]()
![]()
![]()
О (3; -2), R = 6.
б) ![]()
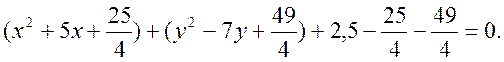
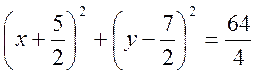
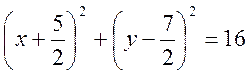
О (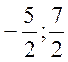 ), R = 4.
), R = 4.
Математический диктант.
1. Записать координаты данных точек А, В, С (изображены на доске).
2. Построить данные точки в системе координат А(-3; 0), В(3; -1), С(2; -4).
3. Записать формулы:
а) координаты середины отрезка;
б) расстояние между точками;
4. Записать уравнение окружности с центром:
а) в начале координат;
б) в любой точке.
4. Подведение итогов урока и домашнее задание.
Домашнее задание: № 26, № 22.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.