КОНСПЕКТ УРОКУ З АЛГЕБРИ
Тема: “Формула коренів квадратного рівняння”.
Мета: навчити учнів розв’язувати квадратні рівняння за формулою коренів квадратного рівняння; розвинути в учнів вміння застосовувати подану формулу до розв’язання квадратних рівнянь; виховати логічне мислення, культуру і акуратність запису.
1. Організаційний момент (3 хв.).
2. Актуалізація знань учнів (18 хв.).
3. Виклад нового матеріалу (13 хв.).
4. Закріплення нового матеріалу (15 хв.).
5. Завдання додому (2 хв.).
6. Підсумок уроку (2 хв.).
1. Організаційний момент.
Вітаюсь. Пропоную сісти і приготуватись до уроку, дістати зошити з домашнім завданням. Оглядаю клас: чи всі сидять на своїх місцях, чи порядок на столах.
2. Актуалізація знань учнів.
Що називається квадратним рівнянням?
Квадратним рівнянням називається рівняння виду ах2+вх+с=0,
де х – змінна, а, в, с – деякі числа, причому а ![]() 0.
0.
Якщо хоча б один з коефіцієнтів квадратного рівняння рівен нулю, то як назвається таке рівняння?
Таке рівняння називвається неповним квадратним рівнянням.
Ми навчилися з вами розв’язувати неповні квадратні рівняння, а також квадратні рівняння методом виділення квадрату двочлена.
3. Виклад нового матеріалу.
Розв’язування кввадратних рівнянь виділення квадрату двочлена часто приовдять до проміжних перетворень. Тому розв’язують рівняння в загальному вигляді і в результаті одержують формулу коренів. Потім цю формулу використовують при розв’язанні будь-якого квадратного рівняння.
Розв’яжемо квадратне рівняння
ах2+вх+с=0 (1)
Розділивши обидві його частини на а, одержимо рівносильне йому рівняння
х2+в/ах+с/а=0.
Первторимо це рівняння:
Рівняння (2) рівносильне рівнянню (1). Число його
коренів залежить від знаку дробу 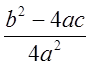 . Так як а
. Так як а ![]() 0, то 4а2 – додатнє
число, тому знак цього дробу визначається знаком його чисельника, тобто виразу
0, то 4а2 – додатнє
число, тому знак цього дробу визначається знаком його чисельника, тобто виразу ![]() . Цей вираз називаєтьс дискримінантом
квадратного рівняння (1). Його позначають буквою
. Цей вираз називаєтьс дискримінантом
квадратного рівняння (1). Його позначають буквою
, тобто
Запишемо рівняння (2) у вигляді:
Розглянемо тепер різні можливі випадки в залежності від дискримінанту.
1) Якщо
Таким чином в такому випадку рівняння (1) має два кореня:
2) Якщо , то рівняння (2) матиме вигляд:
звідси
У цьому випадку рівняння (1) має один корінь 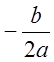 .
.
Формулою коренів квадратного рівняння можна користуватися і в цьому випадку. Дійсно, при Д = 0 ця формула приймає вигляд:
3) Якщо , то значення дробу від’ємне і тому рівняння
а також рівняння (1) не мають коренів. Таким чином, в залежності від дискримінанта, квадратне рівняння може мати два корені (при Д>0), один корінь (при Д = 0) або не має коренів (при Д<0).
При розв’язанні квадратного рівняння за формулою (1) слід поступати слідуючим чином:
1) обчислити Д і порівняти його з нулем;
2) Якщо дискримінант додатній або рівний нулю, то скористуватися формулою коренів, якщо дискримінант від’ємний, то записати, що коренів немає.
Розв’яжемо рівняння:
12х2+7х+1=0;
9х2-14х+5=0;
4. Закріплення нового матеріалу.
Знайти корені рівняння:
(2х-3)(5х+1)=2х+2/5;
(3х-1)(х+3)=х(1+6х);
5. Завдання додому.
Розв’язати рівняння: 8х2-14х+5=0;
(х+4)2=3х+40;
(2х-3)2=11х-19.
6. Підсумок уроку.
Скажу, що ця тема дуже важлива і потрібна для майбутнього. Наголошу на тому, щоб учні вивчили теорію. Оціню відповіді і попрощаюсь з дітьми.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.