Задача 1
Вінні – Пух з П’ятачком відправилися до Сови на день народження. Сова жила на високому дубі. П’яточок ніс в подарунок п’ять однакових баночок меду, а Вінні – Пух повітряну кульку. Ця кулька може за один раз підняти або Вінні – Пуха і дві баночки меду, або П’ятачка з трьома баночками меду, або п’ять баночок меду. Коли друзі підійшли до дуба, Вінні сказав:
- Кулька не зможе підняти нас з баночками меду. Давай сові подаруємо лише повітряну кульку. Доречі, скоро в мене день народження...
П’ятачок вічливо спитав:
- А може кулька підніме нас обох за один раз?
Як би ти відповів на це питання?
Задача 2
Здогадайтеся, які цифри потрібно поставити на місці сніжинок.
* * 5
*
4 *
3 * *
* 2 * *
1 * * * *
Квадрат розділено на дев’ять клітонок. В двох з них поставили червону та синю цятку. Розмістити в кожній з останніх клітинок квадрата по одній з цяток або червоного або синього корьору, або зеленого, але так, щоб в кожному стовпці і в кожному ряді були цятки різного кольору.
|
Синій |
||
|
червоний |
||
Між деякими цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 постав знаки додавання так, щоб утворилось 99. Знайди три способи рішення.
Аня, Боря, Віра та Гена всього спіймали 10 жабок, кожний з дітей сніймав різну кількість жабок. Аня спіймала найбільше від всих, а Віра – найменше від всих. Хто спіймав більше жабок, дівчанкачи хлопчики?
Постав числа 6, 5, 4, 3, 2, 1 в кружки так, щоб сума чисел вздовж кожної прямої рівнялась 12.
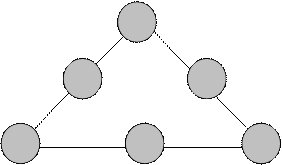 |
а) першу половину шляху мотоцикліст проїхав зі швидкістю 60 км/год., другу - зі швидкістю 30 км/год. Яка його середня швидкість? (Відповідь: 40 км/год.)
б) знайти 4 – значне число, яке при діленні на 251 дає в остачі 201, а при діленні на 252 дає в остачі 194 (Відповідь:1958).
в) дописати до 584 справа дві цифри так, щоб отримане 5 – значне число ділилось на 3, на 7, на 11. (Відповідь: 58 443).
г) Довести, що для будь – якого цілого п число п5- 5п3+ 4п ділиться на 120.
д) Довести, що різниця квадратів двох послідовних непарних чисел ділиться на 8.
8.Подміркуй!
а) Яка із хорд, що проходить через дану точку в нутрі круга, найменша?
б) На які цифри можуть закінчуватися точні квадрати?
в) Назва якої кривої є в той же час літературним терміном?
9. Куди зник гривеник?
У
двох корзинах знаходилось по 30 яблук. Із першої корзини яблука повинні були
продаватися по 2 штуки на 10 коп., а з другої по 3 штуки на 10 коп. Так як в
першій корзині було 15 пар яблук, то за них можна було отримати 1 грн. ![]() 50 коп. Очевидно за яблука із другої
корзини можна було отримати 1 грн. (30:3 = 10; 10
50 коп. Очевидно за яблука із другої
корзини можна було отримати 1 грн. (30:3 = 10; 10![]() 10
= 100коп.)
10
= 100коп.)
Продавець
розмірковував так, що якщо із першої корзини він візьме два яблука, а із другої
– 3 яблука, то за ці яблука він повинен отримати 20 коп. Тому продавець вирішив
знімати всі яблука разом і продавати кожні 5 штук за 20 коп. Після продажу всіх
яблук продавець виявив у себе 2 грн. 40 коп. Замість 2 грн. 50 коп. Стали
перевіряти: в 60 яблуках міститься 12 п’яток. 60:5 = 12; 12![]() 29 = 240 (коп.) Куди зникли 10
копійок?
29 = 240 (коп.) Куди зникли 10
копійок?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.