Арифметична прогресія: План-конспект уроку з алгебри

Міністерство освіти і науки України

Полтавський державний педагогічний університет

ім. В.Г.Короленка

План-конспект

уроку з алгебри на тему:

“Арифметична прогресія:

подання нового матеріалу”

підготували студенти групи МІ-33

фізико-математичного

факультету

Мамон Олександр

Полтава 2003

Тема уроку: арифметична прогресія.

Мета уроку: актуалізувати у учнів знання з теми “послідовність”. Ввести поняття арифметичної прогресії, ознайомити з основними формулами;

сформувати основні навички роботи з формулами n-го члена арифметичної прогресії і суми членів арифметичної прогресії;

виховати уважність і наполегливість.

Тип уроку: урок засвоєння нових знань.

Основні навчальні методи: вправи і правила.

Обладнання і матеріали: дошка, крейда, підручники.

Структура уроку:

Етапи уроку	Організаційний момент	Актуалізація опорних знань	Вивчення нового матеріалу	Підсумок уроку	Домашнє завдання
Напрямки діяльності
Час	2 хв.	10 хв.	25 хв.	3 хв.	5 хв.
Програмова інформація	Повідомлення теми, мети уроку, а також подяки вчителя	Перевірка знань з теми послідовність	Основні правила і формули з теми алгебраїчна прогресія	Повторення основних правил і формул з нової теми	№220, №226, №234, №236 і теорія
Обладнання	Дошка, крейда	Дошка, крейда, підручник	Дошка, крейда, підручник	Підручник	Підручник
Ситуативне управління і контроль	Встановлення готовності учнів до уроку. Перевірка відсутніх	Опитування учнів	Викладення теорії з паралельним виконанням завдань	Висновок уроку, повторення основних правил	Запис завдання у щоденник
Робота з деформаціями	Позитивний настрой учнів завдяки привітності вчителя	Усне опитування комбінується з роботою біля дошки	Заохочення до роботи учнів, які пасивні на уроці	Звернення уваги учнів на недоліки уроку	Наголошення на перевірці домашнього завдання на наступному уроці

Етап №1. Організаційний момент.

Вчитель заходить до класу, робить невелику паузу, чекаючи поки учні заспокояться, потім вітається.

Слова вчителя: “Хочу з самого початку висловити подяку від свого імені та імені директора школи тим учням, які в неділю відвідали стадіон “Ворскла”.

Потім вчитель приступає до повторення минулої теми.

Етап №2. Повторення і актуалізація базових знань.

Слова вчителя: “Перш ніж перейти до вивчення сьогоднішньої теми, ми пригадаємо матеріал, який вивчали на попередніх уроках”.

Вчитель викликає до дошки одного учня. Просить, його, спочатку записати послідовність парних натуральних чисел, потім послідовність непарних натуральних чисел і послідовність чисел обернених до натуральних.

Відповіді повинні мати вигляд:

1)  2,4,6,8,10,...

2)  1,3,5,7,9,...

3) 

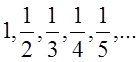
Вчитель просить назвати учня означення “члена послідовності”. Потім просить вказати 2-й і 4-й член кожної із трьох послідовностей.

Викликавши до дошки слідую чого учня вчитель просить його просить його пронумерувати всі члени послідовності. Потім запитує учня в скільки разів кожний член послідовності більший від свого порядкового номера. Коли учень дає відповідь, то вчитель просить його записати формулу для n-го члена послідовності. Потім самостійно зробити це і для інших послідовностей.

Слова вчителя:” Наша слідуючи вправа буде обернена до попередньої”. Він викликає ще одного учня до дошки і зачитує вправу.

№207.

Напишіть кілька членів послідовності n-й член якої  Знайдіть

Потім вчитель просить дати означення зростаючої і спадної послідовності.

На завершення повторення вчитель викликає ще одного учня до дошки і задає йому запитання: “Чи однозначно задають послідовність її перші члени”. Після відповіді просить розв’язати учня наступну вправу.

Вправа.

Напишіть дві різні формули для n-тих членів послідовностей, перші члени яких: 1,3,5,7. Відповідь:.

Етап №3. Ознайомлення з новим матеріалом і первинне його закріплення.

Слово вчителя: “Зараз, після повторення теми послідовностей ми перейдемо до вивчення не менш цікавої і дуже схожої теми “Арифметичної прогресії”. Я прошу Вас досить серйозно віднестись до вивчення сьогоднішньої теми. Оскільки вона матиме дуже важливе значення у подальшому вивченні алгебри. Дуже широко алгебраїчна прогресія застосовується також в фізиці, і навіть у багатьох природничих науках”.

Вчитель викликає учня до дошки і просить його записати послідовність перший член якої 5, а кожний інший на 3 більший від попереднього

                                 5,8,11,14,17,20,23,...

Слово вчителя: “Отже ми бачимо послідовність кожний член якої більший від попереднього на стале число (в нашому випадку це 3), такі послідовності ще називають арифметичною прогресією”. Вчитель просить усно сформулювати означення арифметичної прогресії. Потім сам, ще раз його точно називає.

Озн. “Арифметичною прогресією наз. послідовність кожний член якої, починаючи з другого, дорівнює попередньому члену до якого додають одне й те саме число.”

Просить, ще двох учнів повторити це означення.

Слова вчителя: “Ми бачимо, що кожний член арифметичної прогресії більший від попереднього на деяке стале число. Це число наз. різницею арифметичної прогресії і позначається d.”

Потім викликає учня до дошки і просить знайти різницю арифметичної прогресії: 1,5,9,13,…  . В:4. Запитує у учня чи може він написати загальну формулу для обчислення різниці арифметичної прогресії.

Наступному учню вчитель задає інше завдання:  написати арифметичну прогресію.

Слова вчителя: “Таким способом знаючи перший член арифметичної прогресії і різницю арифметичної прогресії ми можемо знайти послідовно 2,3,4,5 члени послідовності. А якщо ж нам потрібно знайти 100-й член послідовності, то у нас будуть дуже громіздкі і довгі обчислення. Спробуємо знайти більш швидкий і раціональніший спосіб знаходження n -го члена арифметичної прогресії.”

Вчитель просить учня записати чому рівні  арифметичної прогресії.

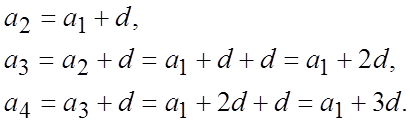
Слова вчителя: “За аналогією ми можемо написати, що   . Тепер спробуй записати формулу для знаходження n-го члена арифметичної прогресії.”

“Зараз, щоб трохи закріпити матеріал наступний учень розв’яже вправу на застосування даної формули.”

Завдання:

В:61.

Наступний учень розв’язує наступне завдання.

Завдання: (не обов’язково).

З’ясувати чи є число х=–122 членом арифметичної прогресії ()

23; 17,2; 11,4; 5,6;…

Розв’язання.

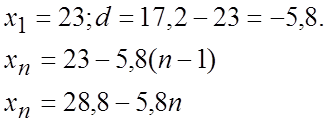
“Число –122 є членом арифметичної прогресії, якщо існує таке натуральне n, при якому значення виразу  Розв’яжемо це рівняння. Одержимо n=26. Отже число –122 є 26-м членом заданої арифметичної прогресії.”

Слова вчителя: “За допомогою ариф. прог. можна робити такі обчислення, які на перший погляд здаються досить складними. Так, наприклад, нам треба знайти суму перших 100 натуральних чисел. Зробимо це не додаючи безпосередньо числа.

Позначимо суму через S і запишемо її двічі,

S=1+2+3+…+98+99+100,

S=100+99+98+…+3+2+1.

Кожна пара чисел, розміщених одне під одним, у сумі дає 101. Кількість таких пар 100. Тому додавши рівності почленно, дістанемо:

                                 2S=101*100; S=(101*100)/2=5050

Отже 1+2+3+…+99+100=5050.

Саме за допомогою таких міркувань ми можемо знайти суму n перших членів арифметичної прогресії.

Для цього позначимо суму n перших членів арифметичної прогресії через Sn і запишемо цю суму двічі

                                

                 

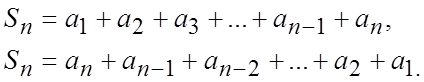
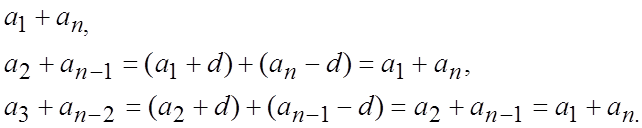
Число таких пар становить n. Тому додавши почленно рівності дістанемо 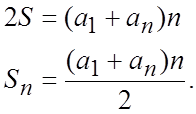 Отже ми з вами вивели формулу суми n перших членів арифметичної прогресії.”

Викликавши іншого учня вчитель запропоновує завдання на застосування даної формули.

Завдання.

Знайти суму перших 20 членів ариф.прог. 5,7,9,…

В: S=480.

Потім вчитель наводить інший вигляд формули суми.

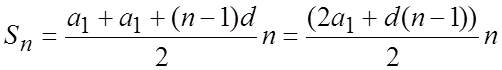
Етап №4. Підсумок уроку.

Слово вчителя: “А тепер давайте повторимо ті основні означення і формули, які ми вивчили на цьому уроці.”

Вчитель запитує декількох учнів означення арифметичної прогресії, різниці ариф.прог. Просить записати формули для  і

Етап №5. Домашнє завдання.

Вчитель просить записати учнів домашнє завдання в зошит.

№220, №226, №234, №236, і теорія.