Види чотирикутників: План-конспект уроку математики

Полтавський державний педагогічний університет

ПЛАН-КОНСПЕКТ УРОКУ

“ВИДИ ЧОТИРИКУТНИКІВ”

Виконав студент

Групи М-33

Йосипенко Юрій

Полтава 2001р.

Клас: 6-ий.

Тема: Види чотирикутників.

Мета:

навчальна – ознайомити учнів з різними видами чотирикутників, сформувати практичні вміння й навички побудови різних видів чотирикутників;

розвиваюча – розвивати здорове сприймання учнів, увагу, уяву, просторове мислення;

виховна – виховувати точність, охайність, культуру праці, естетичний смак.

Матеріально-технічне забезпечення: лінійка, транспортир, олівець, гумка, зошит – у кожного учня; навчальна дошка, крейда, лінійка.

Дидактичне забезпечення: плакати “Види чотирикутників”, “Побудова чотирикутників”.

Тип уроку: комбінований.

Хід уроку:

І. Організаційна частина.

1.  Привітання.

2.  Перевірка присутніх за списком.

3.  Перевірка наявності необхідних інструментів і матеріалів.

ІІ. Перевірка домашнього завдання.

1.  Вибіркове опитування учнів по результатах виконаних вдома задач.

2.  Перевірка наявності виконаних завдань у кожного учня.

3.  Опитування по попередній темі “Паралельні прямі”:

-  Які прямі називаються паралельними?

-  Які особливості побудови паралельних прямих?

-  У яких випадках прямі збігаються?

4.  Оцінювання учнів по результатах домашнього завдання. Відповіді на можливі запитання учнів.

ІІІ. Пояснення нового матеріалу.

Запитання до учнів: чи багато видів чотирикутників вам відомо, хто може назвати чи побудувати один з видів чотирикутників?

Якщо бажаючих учнів немає – викликати одного з учнів до дошки та дати завдання: побудувати чотирикутник ADCD, у якого протилежні сторони паралельні,тобто лежать на паралельних прямих. Допомогти даному учню побудувати таке зображення на дошці:

B                         C

 

A                        D

Учням класу пояснити, що на дошці побудовано паралелограм – чотирикутник, у якого протилежні сторони попарно паралельні, називається паралелограмом.

Всі учні записують визначення в робочі зошити та будують паралелограми. Допомогти учням, яким не вдається побудувати  паралельні сторони.

Викликати до дошки учня та дати завдання побудувати чотирикутник, у якого дві протилежні сторони паралельні, а дві інші не є паралельними. Допомогти учневі побудувати на дошці таку фігуру:

B                  C

 

A                                          D

Учням класу пояснити, що чотирикутник, у якого тільки дві сторони паралельні, називається трапецією. Учні записують в зошити визначення і будують трапеції, вчитель допомагає при необхідності.

Користуючись фігурою на дошці, пояснити учням, що паралельні сторони трапеції називаються її основами, а дві інші сторони – бічними сторонами. Зробити відповідні написи.

Викликати до дошки учня та дати завдання побудувати довільний чотирикутник та сполучити його протилежні сторони:

B                            C

 

A

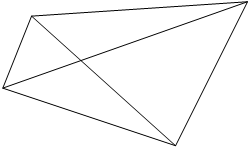D

Учні в зошитах будують таку ж фігуру та записують визначення: відрізок, що сполучає протилежні вершини чотирикутника, називається діагоналлю.

На плакаті “види чотирикутників” допомогти учням визначити діагоналі чотирикутників.

На дошці для побудованих паралелограма і трапеції побудувати висоти цих фігур та пояснити: відрізок, перпендикулярний до протилежних сторін паралелограма, називається його висотою. Відрізок, перпендикулярний до основ трапеції, називається її висотою.

Запропонувати кільком учням повторити визначення.

IV. Закріплення.

Викликати до дошки трьох учнів, кожному дати завдання з підручника Р.М.Литвиненко “Математика”, стор. 42, № 112–114.

В цей час з учнями класу виконувати завдання № 115–116.

По закінченню учнями завдань – вислухати отримані в результаті виконання цих завдань висновки.

Повторити виконання завдань № 117–121 таким же способом.

Наступне завдання – для всього класу – для цього перед уроком на зворотному боці дошки підготувати кросворд та завдання до нього:

1.  Відрізок, перпендикулярний до основ трапеції.

2.  Прямі, що лежать в одній площині і не перетинаються.

3.  Одна з паралельних сторін трапеції.

4.  Інструмент для побудови перпендикулярних прямих.

5.  Чотирикутник, у якого протилежні сторони попарно паралельні.

6.  Чотирикутник, у якого тільки дві протилежні сторони паралельні.

7.  Відрізок, що сполучає протилежні вершини чотирикутника.

8.  Яка лінія проходить через будь-які дві точки, і причому тільки одна?

1
2
3 4 5 6
7
8

Оцінити відповіді учнів, які приймали активну участь. При необхідності задати додаткові питання:

–  Які прямі називають перпендикулярними?

–  Яку роль грають перпендикулярні та паралельні прямі при побудові чотирикутників?

V. Завдання додому.

Прочитати пункт 2.3. підручника. Визначення вивчити напам’ять. Вправи № 122, 123 виконати.

VI. Підсумок уроку.

1.  Оцінювання роботи учнів протягом уроку.

2.  Оголошення виставлених оцінок, аналіз помилок учнів.

3.  Дати відповіді на можливі запитання учнів.

4.  “До побачення!”