Міністерство освіти і науки України
Полтавський державний педагогічний університет
ім. В. Г. Короленка
кафедра математики
План-конспект уроку з алгебри
„ Формули зведення. Тригонометричні функції половинного аргументу”
підготував
студент гр. М-52
фізико-математичного
факультету
Демидченко Ю. В.
Методист
старший викладач
Севрюк І. В.
Полтава 2005
Тема: Формули зведення. Тригонометричні функції половинного аргументу.
Мета:
· Навчальна: навчитися розв’язувати тригонометричні тотожності, використовуючи формули зведення та функції половинного аргументу;
· Розвивати пам’ять, увагу, уяву, логічне мислення, формувати уміння і навички розв’язування задач;
· Виховувати пізнавальний інтерес, охайність, терплячість.
Тип уроку: вивчення нового матеріалу, засвоєння вивченого.
Методи і прийоми: бесіда з учнями, робота з підручником.
Обладнання: дидактичний матеріал.
План уроку.
1.Організаційний момент (2 хв)
2.Перевірка домашнього завдання (4 хв)
3.Повідомлення теми і мети (2 хв)
4.Актуалізація опорних знань (4 хв)
5.Вивчення нового матеріалу (14 хв)
6.Закріплення вивченого(14 хв)
7.Підсумки (3 хв)
8.Домашнє завдання (2 хв)
Хід уроку
1.Організаційний момент.
2.Перевірка домашнього завдання.
Чотири учні на дошці записують розв’язок і пояснюють чому саме така відповідь. Інші звіряються.
3.Повідомлення теми і мети.
Сьогодні ми будемо поглиблювати знання з розділу „Тригонометричні функції” і тема нашого уроку називається „Формули зведення. Тригонометричні функції половинного аргументу”.
4.Актуалізація опорних знань.
- назвіть координатні чверті, в яких ![]() додатні;
додатні;
- назвіть співвідношення між тригонометричними функціями одного й того самого аргументу;
- назвіть формули подвійного аргументу.
5. Вивчення нового матеріалу.
1) Якщо аргумент має вигляд 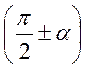 або
або
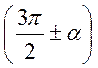 , то назва функції змінюється на
кофункцію, тобто
, то назва функції змінюється на
кофункцію, тобто ![]() і навпаки; якщо ж аргумент
і навпаки; якщо ж аргумент
![]() , то назва не змінюється;
, то назва не змінюється;
2) Перед утвореною функцією ставиться той знак, який має функція, що перетворюється за формулою зведення.
Щоб одержати функції половинного аргументу використаємо такі формули:
![]()
![]()
позначимо ![]() через
через ![]() , тобто
, тобто ![]() ,
тоді
,
тоді
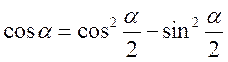
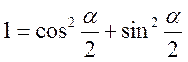
почленно додамо і віднімемо від другої першу одержимо:
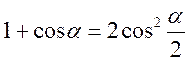
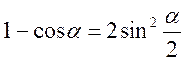
отже,
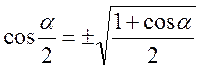 ;
;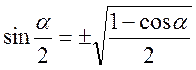 ;
;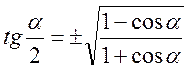 ;
;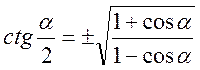
Ці формули ще називають формулами пониження степеня, бо вони дають змогу замінити квадрати тригонометричних функцій на їх перші степені.
6.Закріплення вивченого.
Спростити вираз:
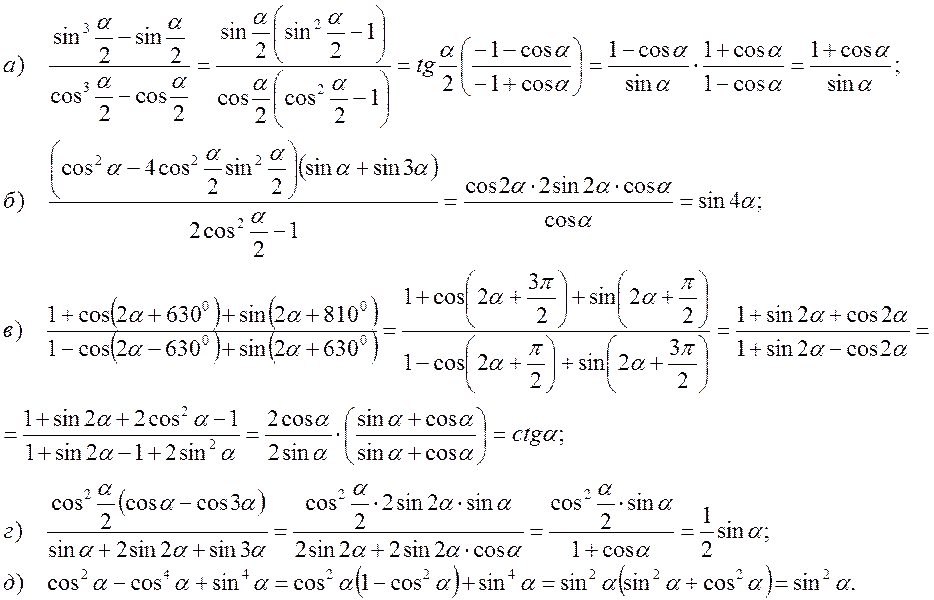
7.Підсумки.
Учні узагальнюють вивчене на уроці:
1) Якщо аргумент має вигляд 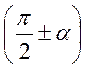 або
або
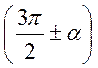 , то назва функції змінюється на
кофункцію, тобто
, то назва функції змінюється на
кофункцію, тобто ![]() і навпаки; якщо ж аргумент
і навпаки; якщо ж аргумент
![]() , то назва не змінюється;
, то назва не змінюється;
2) Перед утвореною функцією ставиться той знак, який має функція, що перетворюється за формулою зведення.
Формули половинного аргументу:
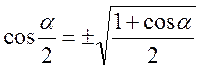 ;
;
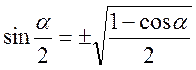 ;
; 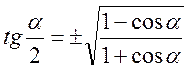 ;
;
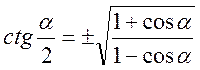 .
.
8.Домашнє завдання. §10
1) Обчислити: 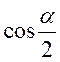 ,
якщо
,
якщо 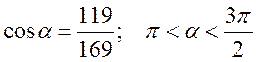
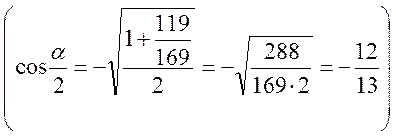
2) Спростити вираз:
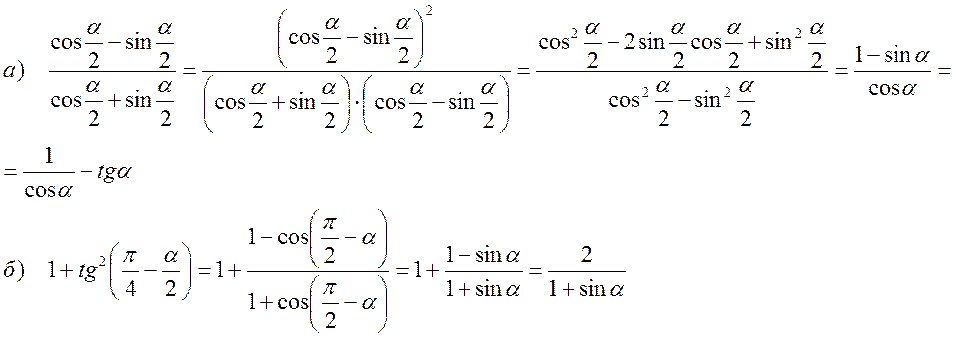
3) Довести тотожність:
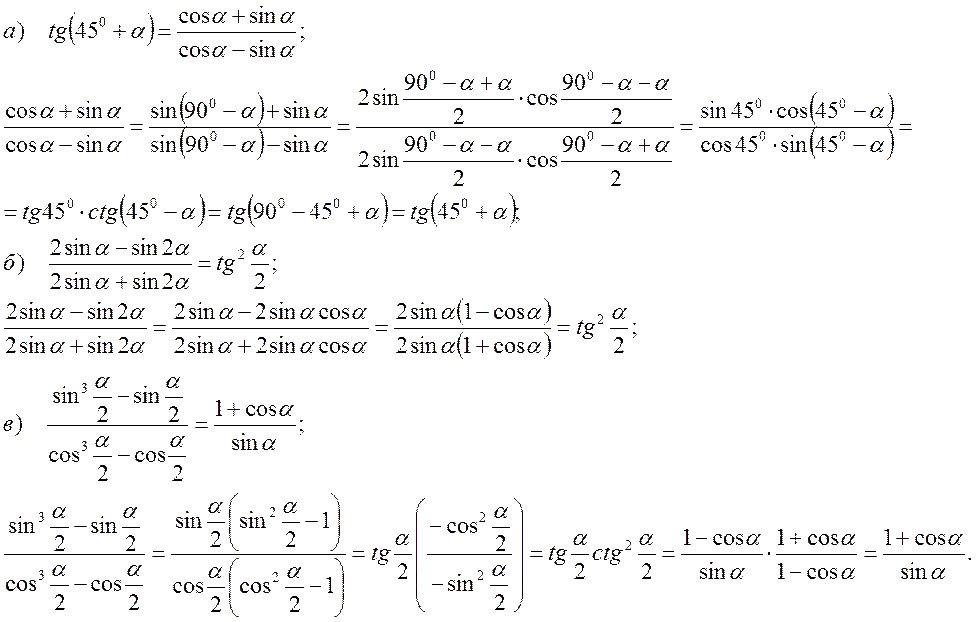
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.