Розробка для факультативного або самостійного вивчення теми "Теорія графів" учнями 8-11 класів

ЗМІСТ

Вступ                                                                                  3

1.  Основні  поняття  теорії  графів.                              4

1.1.  Поняття графа.                                                       4

1.2.  Маршрути , ланцюги  і  цикли.                            4

1.3.  Орієнтовані  графи.                                               6

2.  Основні  задачі теорії графів.                                    8

2.1.  Задача  про  друковану  схему.                      8

2.2.  Задача  про плотер.                                                11

2.3.  Задача  про  розсильного.                                      13

2.4.  Задача  про  призначення.                                     19

Висновки                                                                            23

Література                                                                          24

Додаток                                                                              25

Вступ

                Моя  тема  “ Теорія  графів “  актуальна  тим , що  у  шкільній  програмі  графи  не  вивчаються . Учні  самостійно  не  можуть  опрацювати  цю  тему .  Моя  робота  допоможе  їм  зрозуміти  матеріал . Існують  такі  задачі , які  можуть  розв‘язуватись   тільки  за  допомогою  теорії  графів , а   існують  і  такі ,  які  розв‘язуються  й  іншими  методами , але  цей  буде  легше  для  розуміння . Задачі , які  розв‘язуються  за  допомогою  теорії  графів , сприяють  розвитку  уваги  та  логічного  мислення  в  учнів .

1. Основні поняття  теорії  графів

1.1 Поняття графа

Означення. Простим  графом  G  називається  система , що  складається  з  непорожньої  множини  V  і  множини  U  деяких  невпорядкованих  пар  елементів  з  V.

Коротко  це  позначають  так : G = (V ; U ) .

На  малюнку 1 наведено приклад графа ( простого ).

Елементи  множини  V  будемо  зображати точками  на  площині  і  називати  їх  вершинами, а  множини  U  зображатимемо  лініями (зокрема  відрізками ) і  називатимемо  ребрами  графа . Малюнок , який  при  цьому  дістанемо , також  називатимемо  графом.

  Якщо  ребро  сполучає  вершини   Vr   i  Vs , то  кажуть , що  вони  належать  цьому  ребру , а саме  ребро  відповідно  належить  вершинам  Vr  i  Vs .При цьому  вершини  Vr  i  Vs  називаються  суміжними . Аналогічно  два  різних  ребра  називаються  суміжними , якщо  вони  мають  хоча  б  одну  спільну  вершину . Кожне  ребро  суміжне  саме  собі .

1. 2 Маршрути , ланцюги і цикли

Розглянемо  поняття , які  відіграють  першорядну , фундаментальну  роль  у  теоретичних  питаннях  і  в  практичному  застосуванні  графів.

Означення1. Скінченна  послідовність  суміжних  ребер ( не  обов‘язково  різних )  графа  G , тобто  така  послідовність , в  якій  кожне  ребро , починаючи  з  другого , суміжне  з  попереднім , називається маршрутом  в  G .

Кожне  ребро  є  маршрут . Маршрути  зручніше  позначати  як  послідовності  вершин , через  які  проходить  маршрут . Щоб  підкреслити , що  маршрут  не  має  орієнтації ( тобто  маршрут  з  вершини  Vs  в  вершину  Vr   є  одночасно  маршрутом  з  Vr    y  Vs , ці  вершини  називають  кінцевими  вершинами  маршруту ), позначення  вершин  виділятимемо  рисками .

Довжиною  маршруту  називається число  ребер  у  ньому , однакові  ребра  лічать  стільки  разів , скільки  разів  вони  входять  у  маршрут .

Поняття  маршруту  досить  широке  і  є  допоміжним  для  введення таких  основних  понять, як  ланцюг і цикл .

Означення 2. Ланцюгом  називається  маршрут , в  якому  всі  ребра  різні .

Означення3. Ланцюг, в  якому  кінцеві  вершини  Vr  i  Vs   збігаються , називається  циклом .

Ланцюг  (відповідно  цикл ) , в  якому  всі  вершини  різні , називається  простим , або  елементарним .

Означення 4.Граф  G  називають  зв‘язним , якщо  будь – які  його  вершини  можна  сполучити  хоча  б  одним  ланцюгом .

Незв‘язні  графи  складаються з  окремих  “ кусків “ , компонентів   зв‘язності , кожний  з  яких  є  зв‘язним графом .

Означення 5. Зв‘язний  граф  G  без  циклів називається  деревом .

Незв‘язний  граф  без  циклів  називається  лісом , кожний  компонент  зв‘язності  такого  графа  буде  деревом .

1.3 Орієнтовані графи

   Означення. Орієнтованим  графом (скорочено  орграфом )  О  називається  система , яка  складається  з  непорожньої  множини  V  i  непорожньої  множини  P  деяких  пар  елементів  з  V .

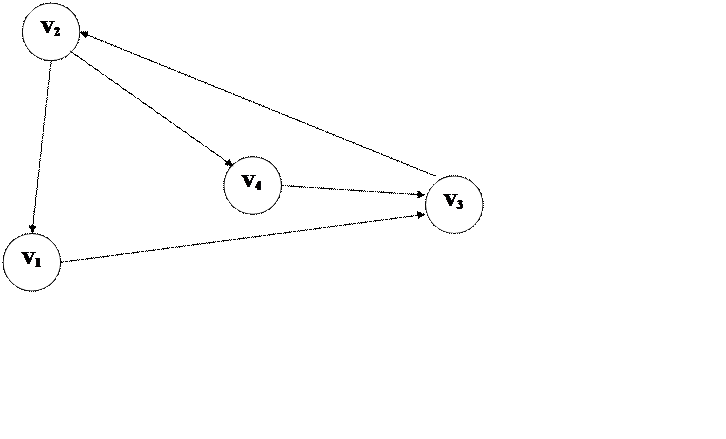Поняття  і  терміни , які  використовуються  при  вивченні  графів ,  переносять  на орграфи.  Елементи  множини  V  називають  вершинами , а  множини  P  дугами. Вершини  орграфа  зображатимемо  на  площині  точками, а  дуги  стрілками, які  йдуть  у  напрямі  від  першої  компоненти  пари  до  другої.

Мал.1

Орієнтованим маршрутом (скорочено ормаршрутом) в орграфі О називається скінченна послідовність таких суміжних дуг, що в кожну вершину, починаючи з другої, заходить дуга з попередньої вершини.

У цьому означенні використовується очевидне припущення про те, що дуги в цих послідовностях сполучені між собою відповідними вершинами.

Орієнтованим ланцюгом (скорочено – орланцюгом) називається ормаршрут, в якому всі дуги різні. Орланцюг, в якому кінцеві вершини V_r i V_s збігаються, називаються орциколом.

Поняття простого орланцюга і орциклу вводиться аналогічно до понять простого ланцюга і циклу.

Поняття зв’язності для орграфів має дві форми: зв’язність (або слабка зв’язність) і сильна зв’язність. Якщо О – деякий орграф, то основою орграфа О назвемо  такий граф G, який дістаємо з О замінною кожної дуги (V_r, V_s) відповідним ребром {V_r, V_s}.

Орграф О називають зв’язним, якщо його основа зв’язна і сильно зв’язним, якщо для будь-яких двох його вершин V_r i V_s існує орланцюг з V_r у V_s і навпаки.

З цього означення випливає, що будь-який сильно зв’язний орграф буде зв’язним, але не навпаки.

Поняття зв’язності і сильної зв’язності орграфів мають багато практичних ілюстрацій. Наприклад, план вулиць міста з одностороннім рухом транспорту можна зобразити деяким орграфом О_m, вершинами якого є перетин вулиць (у тому числі площі), а дугами – відповідні частини вулиць з фіксованим напрямом руху. Якщо такий орграф сильно зв’язний, то можна проїхати з будь-якої частини міста в будь-яку іншу його частину, не порушуючи правила руху. Якщо ж О_m зв’язний (але не сильно зв’язний), то знайдуться хоча б дві такі частини міста, що проїхати з однієї з них в іншу без порушень правил руху неможливо. На практиці на таких ділянках міста дозволяють двосторонній рух або визначають напрям руху так, щоб уникнути порушень правил руху.

2. Основні  задачі теорії графів

2.1 Задача  про  друковану  схему

Друкована схема – це пластинка з будь-якого матеріалу, який є непровідником струму (ізолятора), на якій у виді металевих смужок витравлені струмопровідні доріжки. Перетинатися струмопровідні доріжки не повинні, це викличе замикання електричного ланцюга. Струмопровідні доріжки можуть перетинатися тільки у відведених точках. У ці місця на плату встановлюються необхідні елементи – діоди, тріоди, резистори, конденсатори та інші.

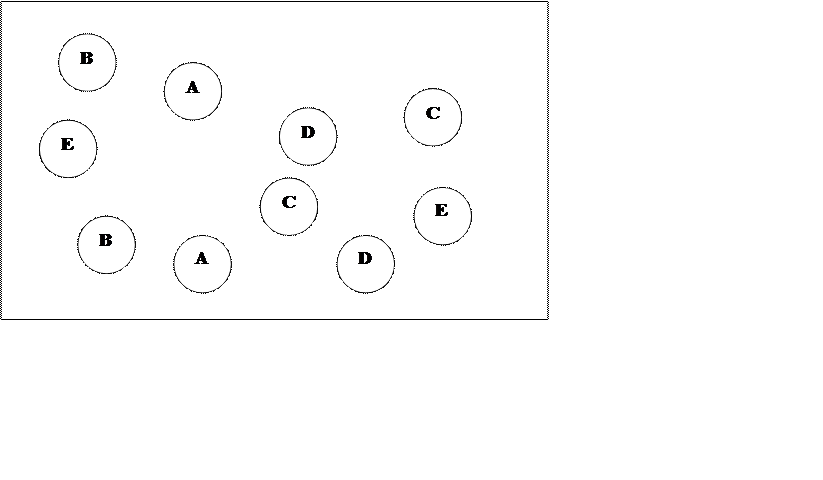
На малюнку 2 намальована частина пластинки, на якій необхідно з’єднати доріжками пари точок, відмічених однією літерою. Виходити за межі пластинки та перетинати її не можна.