ЗАДАНИЯ
В таблице приведены значения х – средние значения встречаемости Х и Уi
(i = 1, 2, ……..10) – средние значения встречаемости У.
Требуется, используя метод наименьших квадратов, подобрать линейную функцию, которая описывает зависимость уi от х.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
х |
1 |
2,5 |
3,0 |
6,5 |
7 |
8,5 |
10 |
15 |
20 |
30 |
|
у1 |
115 |
108 |
102 |
98 |
93 |
89 |
87 |
72 |
65 |
60 |
|
у2 |
11,0 |
10,3 |
9,7 |
9,4 |
8,8 |
8,4 |
8,2 |
6,7 |
6,0 |
5,5 |
|
у3 |
1,15 |
1,08 |
1,02 |
0,98 |
0,93 |
0,89 |
0,87 |
0,72 |
0,65 |
0,6 |
|
у4 |
120 |
113 |
107 |
103 |
98 |
94 |
92 |
77 |
70 |
65 |
|
у5 |
11,5 |
10,8 |
10,2 |
9,8 |
9,3 |
8,9 |
8,7 |
7,2 |
6,5 |
6,0 |
|
у6 |
12,0 |
11,3 |
10,7 |
10,3 |
9,8 |
9,4 |
9,2 |
7,7 |
7,0 |
6,5 |
|
у7 |
135 |
118 |
112 |
108 |
103 |
99 |
97 |
82 |
75 |
70 |
|
у8 |
10,5 |
9,8 |
9,2 |
8,8 |
8,3 |
7,9 |
7,7 |
6,2 |
5,5 |
5,0 |
|
у9 |
12,5 |
11,8 |
11,2 |
10,8 |
10,3 |
9,9 |
9,7 |
8,2 |
7,5 |
7,0 |
|
у10 |
123 |
116 |
110 |
106 |
101 |
97 |
95 |
80 |
73 |
68 |
Соотношение, определяющее линейную функцию имеет вид:
у = кх + в
где к и в – некоторые числа; х – независимая переменная (аргумент),
у – зависимая переменная (функция).
В заданиях требуется найти к и в, при которых линейная функция
у = кх + в достаточно точно отражает результаты экспериментов, приведенные в таблице.
Формулы, выражающие к и в через экспериментальные данные, имеют вид:
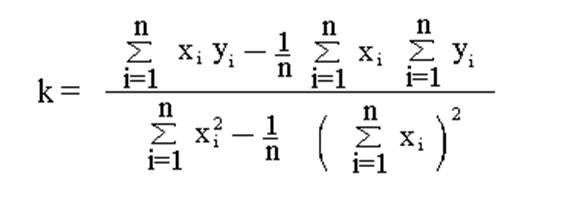
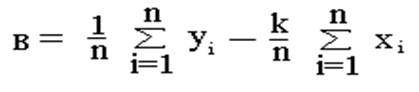
n – количество наблюдений
Пояснения:
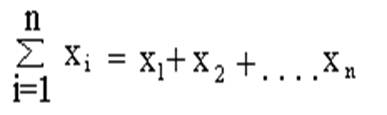
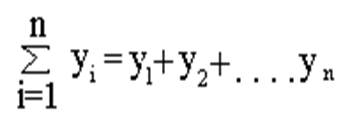
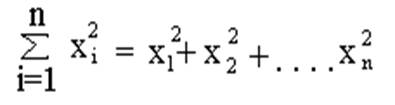
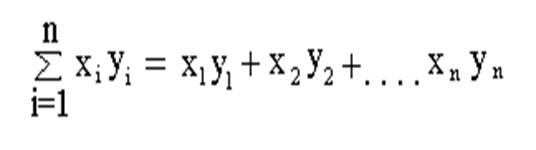
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.