Розробка для факультативного або самостійного вивчення теми "Теорія графів" учнями 8-11 класів, страница 2

мал. 2

Розв’язок знайти не важко. Він приведений на мал. 3.

 

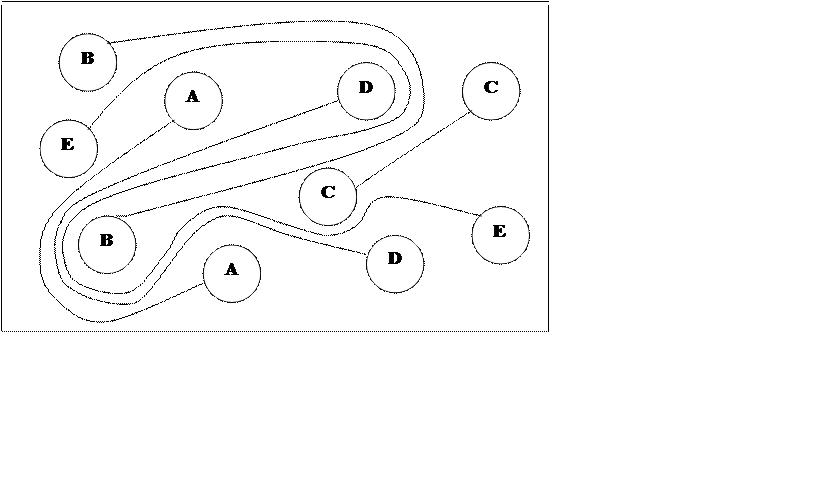мал.3

У ході розв’язку задачі ми займались викреслюванням графа-фігури, яка складається з окремих вершин, з’єднаних дугами. У викресленому графі 10 вершин та 5 дуг.

Чи завжди такого роду задачі розв’язуються так легко ?

Спробуємо розв’язати задачі подібні до цієї та сконструюємо друковану схему, в якій кожну з точок А, В і С необхідно з’єднати з точками F G й Н. Розміщення точок показано на мал. 4. Виходити за межі пластинки заборонено.

 

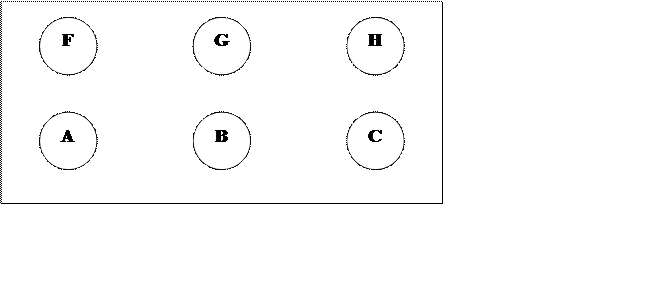
мал.4

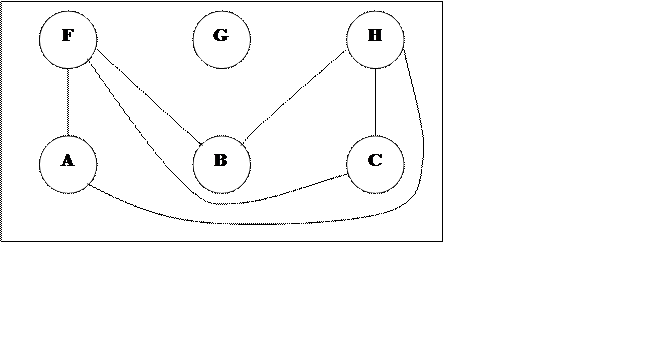
Спроби намалювати таку схему марні. Це неможливо. Доведення видно з мал. 5, де показано, як точки А, В й С з’єднанні з точками Е й G (точка F ще не використана).

 

                                                                ІІІ

                                          І                                      ІІ

мал.5

Шість дуг розбили площину схеми на три залежні області: І, ІІ й ІІІ. Зрозуміло, що точка F повинна знаходитись тільки в одній з них; якщо вона буде знаходитись в області І, то F  неможливо з’єднати з вершиною В, якщо F опиниться в області ІІ, то її неможливо з’єднати з вершиною А, й, нарешті, якщо F буде знаходитись в області ІІІ, то її неможливо з’єднати з вершиною G.

Неймовірний розв’язок, адже у попередній задачі друкована схема здавалась більш складною – у ній 10 вершин, а тут лише 6.

Виникає питання, чи не можна знайти загальний принцип оцінювання таких друкованих схем ? Чи не можна заздалегідь сказати, яку схему можна викреслити, а яку ні. Задача про друковану схему переросла у задачу простого графа. Задача конструкторська виникла перед нами як задача математична, як задача на дослідження властивостей простого графа.

2.2 Задача  про плотер

Добре відомо, що сучасні комп’ютери працюють з різними зовнішніми пристроями, за допомогою яких вони отримують інформацію й виводять її по мірі розв’язування задачі. Одним з таких пристроїв є  плотер. За допомогою плотера комп’ютер викреслює на папері будь-які лінії: графіки досліджуваних функцій, плани та інше. Іноді  використовується кілька кольорів – малюнки виходять яскравими та виразними.

Зрозуміло, що більш легко викреслюється лінія (граф), якщо плотеру не потрібно відривати перо від паперу – він почав викреслювання й веде його, не зупиняючись.

Така задача виникала у теорії графів давно, вона пов’язана з ім’ям видатного математика Л. Ейлера й формується звичайно так: даний простий граф необхідно викреслить не відриваючи олівця від паперу, не обводячи двічі одне й те саме ребро, й повернутись у вихідну вершину графа.

Л. Ейлер у 1736 році показав: якщо всі вершини простого просторового графа парні, то задачу можна розв’язувати.

Парною (непарною) вершиною графа називається вершина, з якої виходить парне (непарне) число ребер.

Якщо дві вершини непарні, то виходячи з однієї непарної вершини, можливо повернутись у іншу, не проходячи по жодному з ребер двічі; якщо непарних вершин 2К, то існує К шляхів, які починаються й закінчуються в непарних вершинах.

На мал. 6 показано граф, який можна обвести, не відриваючи олівець від паперу. У даного графа 6 вершин, й кожна з них парна. Звідкіля починати викреслювання.

мал.6

Існує наступний спосіб викреслювання: в даному графі треба обрати одну область й заштрихувати її; область, яка знаходиться поруч з заштрихованою, проминути (не заштриховувати), а ту, яка має тільки спільну вершину заштрихувати, й так діяти до тих пір, поки всі можливі області не будуть заштриховані.

          У даному випадку вихідний граф після штрихування буде мати вид, непарний на мал. 7.

мал.7

Далі заштрихований граф слід роз’єднати в одній або декілька вершинах так, щоб вийшла однозв’язна (без “дірок”)заштрихована область. У даному випадку роз’єднання приведе до мал. 8, з якого видно, що заштриховану область можна обвести не перерваною лінією, наприклад, колом.

мал.8

Таким чином, теорія графів не тільки дала розв’язання задачі, але й указала метод відшукування необхідного обходу графа. Саме цим математика ще раз показала свою силу.

2.3 Задача  про  розсильного

Маємо К міст, відстані між якими відомі; розсильний відправляється в дорогу із одного з них з тим, щоб пройти всі інші (К-1) міста по одному разу кожне, й повернутись у вихідне місто.

Як знайти найкоротший маршрут ?

 

мал.9

На мал. 9 є приклад схеми району дії розсильного; літерами А, В, С, Д й Е помічені міста. Розсильний починає й завершує свій шлях у місті А.

З цього виходить, що задача про розсильного – це задача про знаходження дороги на графі. Вище вже була розглянута одна задача про дорогу на графі, у ній було необхідно обійти граф, так, щоб дорога  проходила по кожному ребру тільки один раз. Такі маршрути на графі називають ейлерові. У новій задачі треба знайти такий шлях на графі, щоб будь-яка його вершина була пройдена тільки один раз. Такі дороги на графі називають гамільтоновими, в честь ірландського математика У. Гамільтона (1805 - 1865 р.р.).

Вище було сказано про те, що математикам вдалося знайти умови існування ейлерових шляхів на графі й був показаний метод прокладення таких  шляхів. Задача Ейлера розв’язана повністю.

На перший погляд, по аналогії з задачею про відшукання ейлерових  шляхів, задача про знаходження гамільтонових шляхів здається розв’язуваною. Однак це не так: не вдалося сформулювати вимоги, яким повинен відповідати граф, щоб на ньому від вершини до вершини можна було б провести гамільтоновий шлях.

Відомо (це показав сам У. Гамільтон), що каркаси багатьох правильних многогранників є гамільтоновими графами (на них можливо провести гамільтований шлях).

Але існують многогранники, які не є гамільтоновими. Наприклад, ромбічний додекаедр, зображений на мал. 10.

 

мал.10

На цьому графі число вершин, зображених точками 6, а кружками – 8. Розміщені вони на кожній грані чергуючись. Таким чином, побудувати маршрут, при якому перехід від вершини до  вершини супроводжується змінною їх виду, неможливо. (Для цього необхідно, щоб точок і кружків було однакова кількість).

Ще раз підкреслимо, що в загальному випадку задача про будування гамільтонових шляхів (а також і задача про розсильного) не розв’язана так, як цього хотіли математики.

Головна невдача в тому, що не знайдені умови існування такого шляху.

Взагалі кажучи, розв’язати цю задачу в принципі просто, оскільки число всіх можливих маршрутів скінчене (наприклад, число маршрутів, які починаються й закінчуються в місті А, дорівнює n = (К – 1) !), але організувати повний перебір всіх без виключення маршрутів, обчислити їх відстань й обрати найкоротший – робота, яка  вимагає великих обрахунків.

Якщо кількість міст невелика, то повний перебір всіх маршрутів, наприклад тих, що починаються й закінчуються в місті А, можна гарно організувати, якщо використати  допоміжний граф-дерево.

Відмітимо одну суттєву обставину: у задачі про рух між містами припускалося, що çАВú – відстань від міста А до міста В дорівнює зворотній відстані çВАú. Однак це не завжди так. Уявіть собі, що автолавка виступає у ролі розсильного й обходить К підприємств міста. Можливо, що деякі вулиці, по яким вона проїжджає, з одностороннім рухом, і це, звісно, порушить умову çАВú = çВАú, адже з А в В він їде по одним вулицям, а з В в А – по іншим.