Лекція №11
Розв’язування комбінаторних транспортних задач
на переставленнях методом гілок та меж
1. Постановка задачі та означення оцінки допустимих множин
Розглянемо комбінаторну транспортну задачу на переставленнях (КТЗП):
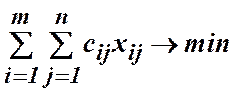 (1)
(1)
за умов
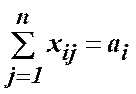 ,
, ![]() ;
(2)
;
(2)
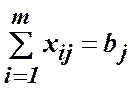 ,
, ![]() ;
(3)
;
(3)
![]() , (4)
, (4)
де ![]() – загальна евклідова множина
переставлень з елементів мультимножини
– загальна евклідова множина
переставлень з елементів мультимножини 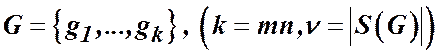 ,
які упорядковані по неспаданню:
,
які упорядковані по неспаданню:
![]() . (5)
. (5)
Нехай деякі змінні задачі (1)-(4) (при
утворенні допустимої підмножини в методі гілок та меж (МГМ)) фіксовані як
елементи з мультимножини ![]() :
:
![]() (6)
(6)
Не обмежуючи загальності, упорядкуємо нумерацію
цих змінних ![]() так, щоб
так, щоб
![]() .
(7)
.
(7)
З умов (6) та (7) маємо також
![]() . (8)
. (8)
Оскільки змінні ![]() визначають
допустиму множину задачі, то їх значення
визначають
допустиму множину задачі, то їх значення ![]() з
(6) не суперечать умовам (2)-(3). Будемо це мати на увазі в наступних
міркуваннях. Упорядкуємо по незростанню не визначені в умові (6) змінні задачі
(1)-(4)
з
(6) не суперечать умовам (2)-(3). Будемо це мати на увазі в наступних
міркуваннях. Упорядкуємо по незростанню не визначені в умові (6) змінні задачі
(1)-(4) ![]() ,
, ![]() ,
та позначимо їх
,
та позначимо їх ![]() :
:
![]() , (9)
, (9)
де ![]() . Таке впорядкування можна зробити не
порушуючи загальності міркувань.
. Таке впорядкування можна зробити не
порушуючи загальності міркувань.
Упорядкуємо по незростанню не використані в
умові (6) елементи мультимножини ![]() , тобто якщо
, тобто якщо ![]() {
{![]() }
– мультимножина використаних в (3.6) елементів
}
– мультимножина використаних в (3.6) елементів ![]() ,
то
,
то ![]() , тобто
, тобто ![]() є
різницею мультимножини
є
різницею мультимножини ![]() та
та ![]() ,
де
,
де ![]() . Упорядкуємо елементи
. Упорядкуємо елементи 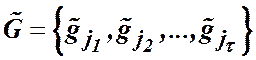 так
так
![]() . (10)
. (10)
Позначимо коефіцієнти цільової функції (1) ![]() з тими ж індексами, що і змінні
з тими ж індексами, що і змінні ![]() , що фігурують в (6) так:
, що фігурують в (6) так: 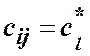 , де
, де ![]() –
коефіцієнт при
–
коефіцієнт при ![]() з (6). Позначимо множину
з (6). Позначимо множину 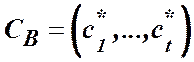 . Коефіцієнти цільової функції (1)
. Коефіцієнти цільової функції (1) ![]() , що стоять при невизначених змінних
, що стоять при невизначених змінних ![]() з (9) позначимо
з (9) позначимо ![]() їх множину позначимо
їх множину позначимо ![]() , де
, де ![]() -
множина всіх коефіцієнтів. Нумерацію серед чисел
-
множина всіх коефіцієнтів. Нумерацію серед чисел ![]() та
та
![]() зробимо, не порушуючи загальності
міркувань, таку, щоб виконувались умови:
зробимо, не порушуючи загальності
міркувань, таку, щоб виконувались умови:
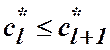
![]() ; (11)
; (11)
![]()
![]() . (12)
. (12)
Оцінку встановлює така теорема.
Теорема 1. Для множини ![]() допустимих
розв’язків задачі (1)-(4), в якій допустимі розв’язки задовольняють умову (6),
в методі гілок та меж за оцінку може слугувати величина
допустимих
розв’язків задачі (1)-(4), в якій допустимі розв’язки задовольняють умову (6),
в методі гілок та меж за оцінку може слугувати величина
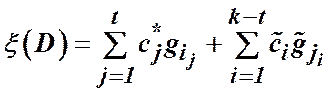 , (13)
, (13)
в якій параметри задовольняють умови (8), (10), (11), (12).
Зауваження до теореми 1. Позначимо першу суму в (13) ![]() та зазначимо, що друга сума в правій
частині виразу (13) є мінімум лінійної функції (з коефіцієнтами
та зазначимо, що друга сума в правій
частині виразу (13) є мінімум лінійної функції (з коефіцієнтами ![]() ) на множині переставлень з
мультимножини
) на множині переставлень з
мультимножини ![]() :
:
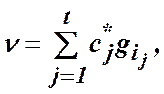
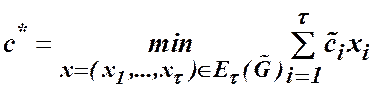 . (14)
. (14)
Отже, (13) з підстановкою (14) набуде вигляду:
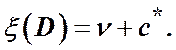 (15)
(15)
Оцінка (13) має таку властивість.
Теорема 2. Нехай ![]() {
{![]() }, де
}, де
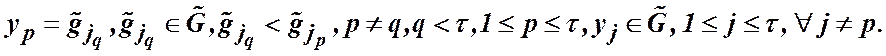 (16)
(16)
Нехай ![]() {
{![]() }, де {
}, де {![]() }
– множина, що містить будь-який з векторів
}
– множина, що містить будь-який з векторів ![]() ,
для яких виконуються умови (16), (10), а
,
для яких виконуються умови (16), (10), а ![]() –
множина допустимих розв’язків задачі (1)-(4), що задовольняють умову (6). Тоді
між оцінками вигляду (13) для множин допустимих розв’язків
–
множина допустимих розв’язків задачі (1)-(4), що задовольняють умову (6). Тоді
між оцінками вигляду (13) для множин допустимих розв’язків ![]() та
та ![]() задачі
(1)-(4) виконується співвідношення:
задачі
(1)-(4) виконується співвідношення:
![]() (
(![]() )
)![]() (
(![]() ). (17)
). (17)
2. Ілюстрація застосування введеної оцінки допустимої множини
Приклад1.Нехай
розглядається задача (1)-(4), та задано ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
,
![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() . Розв’яжемо задачу методом гілок та меж.
. Розв’яжемо задачу методом гілок та меж.
Розв’язок зображено на рис. 1. Пояснення до
рис. 1. ![]() – множина всіх допустимих
розв’язків задачі,
– множина всіх допустимих
розв’язків задачі, ![]() – розрив та продовження
схеми. Галуження виконується так: найменшому коефіцієнту цільової функції
ставиться у відповідність найбільший елемент з
– розрив та продовження
схеми. Галуження виконується так: найменшому коефіцієнту цільової функції
ставиться у відповідність найбільший елемент з ![]() (тобто
(тобто
![]() , бо
, бо ![]() )
і т.д.
)
і т.д. ![]() – поточне рекордне мінімальне
значення цільової функції для відомого допустимого розв’язку.
– поточне рекордне мінімальне
значення цільової функції для відомого допустимого розв’язку. ![]() (
(![]() )
– значення цільової функції для допустимого розв’язку, що отримано
)
– значення цільової функції для допустимого розв’язку, що отримано ![]() -м після
-м після ![]() .
. ![]() – операція заміни поточного рекорду
на новий, коли
– операція заміни поточного рекорду
на новий, коли ![]() . Розгалуження на схемі, що
наведена на рис.1, в методі гілок та меж для прикладу 1 відбувається як
показано на рис., тобто: згори вниз, а на одному рівні – зліва направо, причому
спершу галузиться рівень, якщо це можливо, а потім – перехід вниз на наступний
рівень. Кожен прямокутник схеми відповідає множині допустимих розв’язків
задачі, в яких означені змінні, що показані в ньому, або означені вище чи
лівіше за схемою. Знак
. Розгалуження на схемі, що
наведена на рис.1, в методі гілок та меж для прикладу 1 відбувається як
показано на рис., тобто: згори вниз, а на одному рівні – зліва направо, причому
спершу галузиться рівень, якщо це можливо, а потім – перехід вниз на наступний
рівень. Кожен прямокутник схеми відповідає множині допустимих розв’язків
задачі, в яких означені змінні, що показані в ньому, або означені вище чи
лівіше за схемою. Знак ![]() означає, що прямокутнику,
біля якого він стоїть, відповідає порожня множина допустимих розв’язків. Якщо
означає, що прямокутнику,
біля якого він стоїть, відповідає порожня множина допустимих розв’язків. Якщо ![]() , то допустима множина далі не
галузиться, а відсікається (відкидається). Величина
, то допустима множина далі не
галузиться, а відсікається (відкидається). Величина ![]() –
це оцінка вигляду (13). Допустимі множини, що позначені в схемі
–
це оцінка вигляду (13). Допустимі множини, що позначені в схемі ![]() , згідно з теоремою 2 в схемі методу гілок та меж
можуть не розглядатися, оскільки для них, як для
, згідно з теоремою 2 в схемі методу гілок та меж
можуть не розглядатися, оскільки для них, як для ![]() , існують вже розглянуті множини
, існують вже розглянуті множини ![]() з
з ![]() (
(![]() )
)![]() .
.
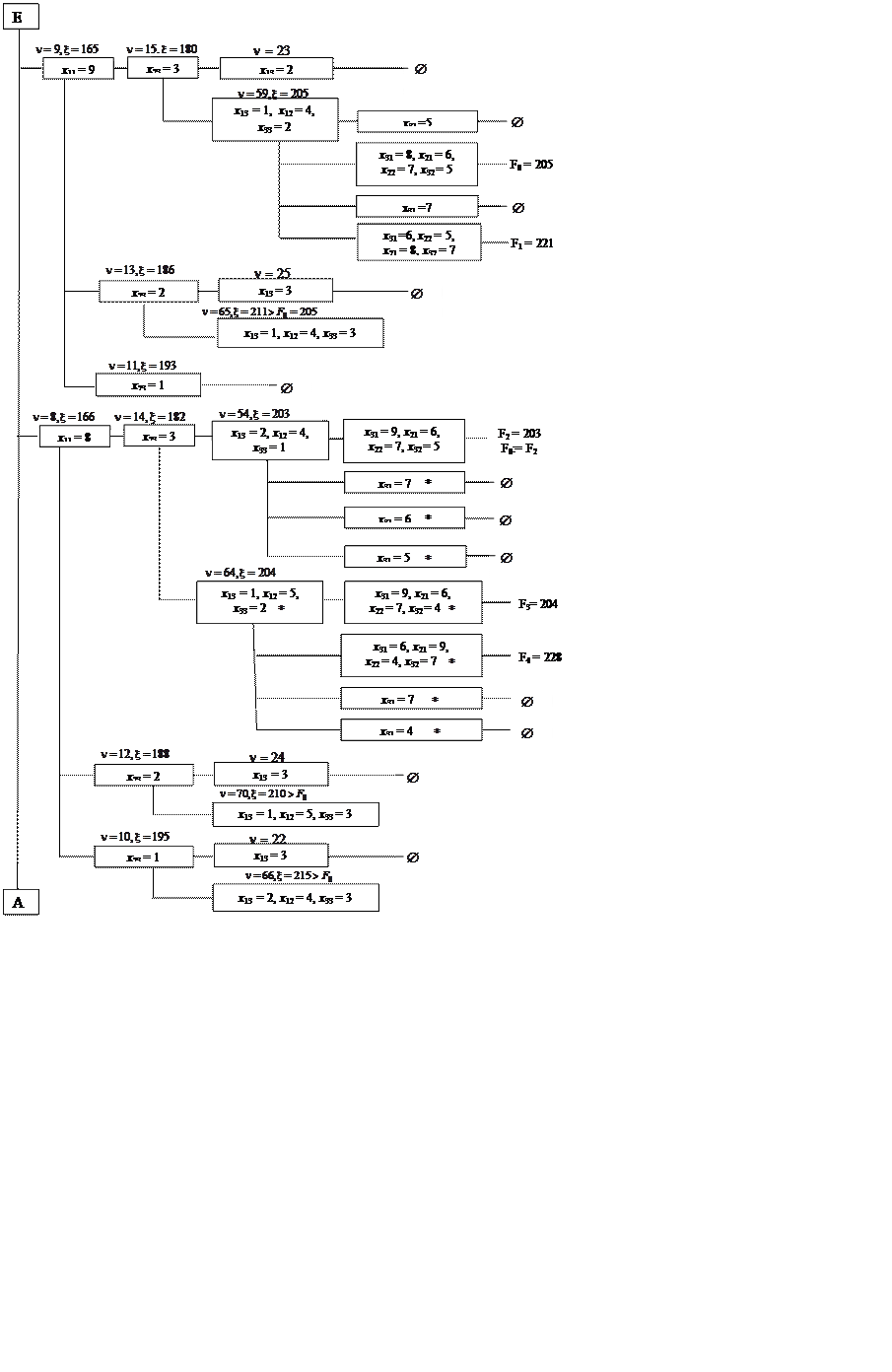
Рисунок 1 – Схема реалізації методу гілок та меж до прикладу 1.

Продовження рисунка 1.
3. Друга властивість оцінки в методі гілок та меж
Покажемо, що оцінка ![]() , що задається формулою (13) має властивість,
яка дозволяє в методі гілок та меж скоротити кількість вершин – допустимих
підмножин, які підлягають подальшому галуженню. Далі, якщо не сказано інше,
використовуємо позначення п.1.
, що задається формулою (13) має властивість,
яка дозволяє в методі гілок та меж скоротити кількість вершин – допустимих
підмножин, які підлягають подальшому галуженню. Далі, якщо не сказано інше,
використовуємо позначення п.1.
Нехай ![]() ,
де
,
де
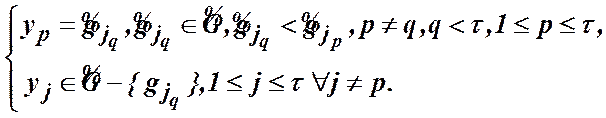 , (18)
, (18)
Нехай за умов (9), (10), (12), (18) з множини ![]() сформуємо дві множини векторів
сформуємо дві множини векторів ![]() та
та ![]() вигляду
вигляду
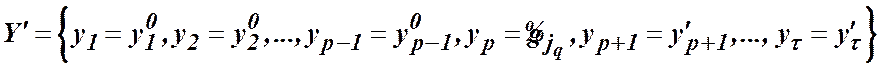 ,
,
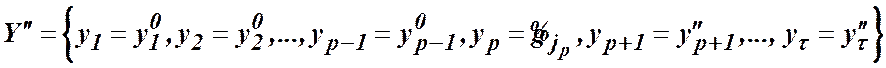 .
.
Зауважимо, що перші ![]() елементів
в
елементів
в ![]() та
та ![]() однакові;
елемент
однакові;
елемент ![]() – це
– це ![]() або
або
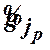 відповідно. Оскільки
відповідно. Оскільки ![]() , то в силу (18)
, то в силу (18) 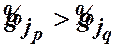 , а з (12) маємо
, а з (12) маємо ![]() .
.
Нехай ![]() – підмножина
допустимих розв’язків, в якій координати допустимого розв’язку, що не є
– підмножина
допустимих розв’язків, в якій координати допустимого розв’язку, що не є ![]() , визначені.
, визначені.
Нехай ![]() ;
; ![]() .
.
Теорема 3. Між оцінками виду (13) для множин ![]() та
та ![]() існує
співвідношення
існує
співвідношення
![]() (19)
(19)
Зауваження. Властивість оцінки (13) для підмножин ![]() та
та ![]() при
галуженні і відсіканні в методі гілок та меж ефективно використовувати для
відсікання множин
при
галуженні і відсіканні в методі гілок та меж ефективно використовувати для
відсікання множин ![]() , коли розглянута множина
, коли розглянута множина ![]() , та
, та 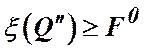 .
.
Приклад 2. Розглянемо приклад 1, застосувавши теорему 3 (див. рис. 2). Пояснення до рис. 2 як і до рис. 1.
Допустимі множини, які позначені ** на рис. 2, згідно
з теоремою 3 в схемі методу гілок та меж можуть не розглядатися, оскільки для
них, як для ![]() , існує вже розглянуті множини
, існує вже розглянуті множини ![]() ,
, ![]() .
.
Останнє свідчить про ефективність властивості, що доведена в теоремі 3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.