Розв’язування комбінаторних транспортних задач на переставленнях методом гілок та меж, страница 4

Продолжение рисунка. 2.

4. Правила відсікання при галуженні в методі гілок та меж для комбінаторних транспортних задач на переставленнях

Теорема 4. (Правило А.) Якщо при галуженні в методі гілок та меж для транспортної задачі (1)-(4) на переставленнях з елементів  допустима підмножина  переставлень визначається заданням певної кількості змінних з , після чого з рівнянь

 ;                                            

 ;                                              

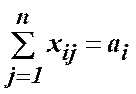
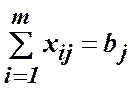
підстановкою визначених змінних отримано два рівняння вигляду

;                                                      (20)

,                                                       (21)

де , і якщо

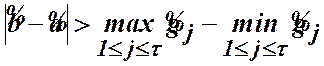,                                 (22)

то множина  відсікається, як така, що не має допустимих розв’язків.

Теорема 5. (Правило В). Якщо за умов правила А 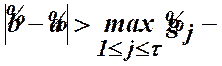 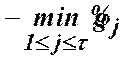 і , такий, що 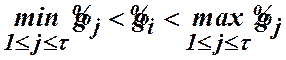, то в (20) та (21)

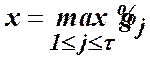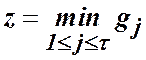; ,                                    (23)

або навпаки

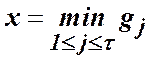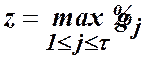; ,                                    (24)

а множину  можна розгалузити задавши  з (23) або з (24).

Приклад 3. Транспортна задача задана так: , а інші умови – в таблиці 1.

Таблиця 1. – Умова прикладу 3.

	6		1		3		15
	5		4		2		60
	15		25		35

Якщо  визначається: ,  (, ) маємо (див. табл. 2):

, 

,

,

.

Таблиця 2. – Перше галуження

	6		1		3		15	5
				10
	5		4		2		60	45
				15
	15		25		35
	15		0		35

Нова мультимножина . При подальшому галуженні . Але скориставшись правилом А маємо:

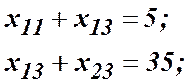
Отже, .

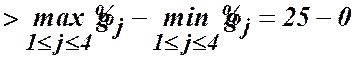Отже, галуження, при якому , не буде, оскільки множина , що визначається ;  відсікається за правилом А.

Повернувшись на вищий рівень галуження, задамо , і отже, . Маємо ситуацію, що представлена в таблиці 3.

	6		1		3		15	10
				5
	5		4		2		60	40
				20
	15		25		35
	15		0		35

Таблиця 3 – Наступне галуження

Маємо: , . Система обмежень набула вигляду:

,

,

,

.

Врахування першої та останньої рівності дає: .

За правилом 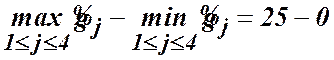В  та в  існують  такі, що: . Отже, можна покласти , . Це дає одночасно , . Отримано одноелементну множину  (тобто допустимий розв’язок), на якому маємо значення цільової функції .

Цей приклад ілюструє застосування правил А та В при галуженні допустимих підмножин.

Теорема 6. Якщо при утворенні допустимої підмножини  з рівнянь-умов

 ;                                                    

 ;                                                      

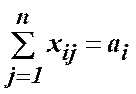
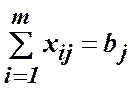
утворилась система  обмежень з  невідомими, то, не проводячи подальших галужень, її розв’язують, що дає одне з трьох:

1)  система несумісна:  – відсікаємо;

2)  ранг системи , система сумісна – отримуємо одноелементну підмножину – допустимий розв’язок;

3)  система має ранг менший  – отримуємо підмножину , яку можна галузити далі.

Література

1. Ємець О.О. Транспортні задачі комбінаторного типу: властивості, розв'язування, узагальнення: монографія / О.О. Ємець, Т.О. Парфьонова. - Полтава: ПУЕТ, 2011. - 174 с.