Зворотні кругові тригонометричні функції

и) графік на проміжку (— 1; 0) опуклий, а на проміжку (0; 1) — увігнутий,   тому  що

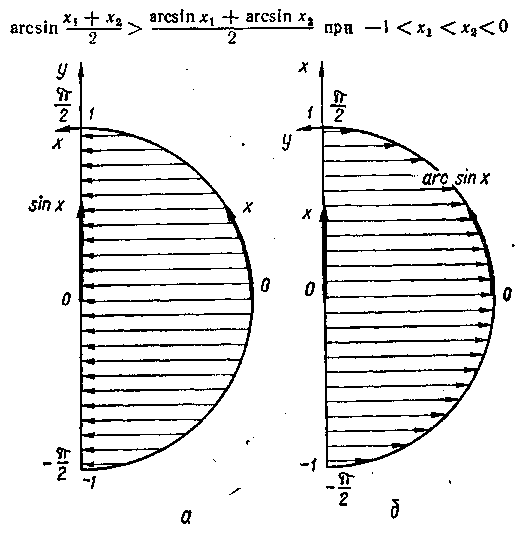
Графік функції в = arcsin x приведений на мал. 15.2.

Арккосинус — функція, зворотна косинусові; якщо х = cos y,ioy= arccos x (мал. 15.3).

Основні властивості функції в = = arccos x:

а)  визначена    при   — 1 <: х < 1;

б)  змінюється   від   0   до   я,   тобто
 ПРО •< arccos х < я,    і   є   непре­
 рывной  і  обмеженої;

в) задовольняє умові arccos (— х)= = я —arccos х, тобто ні парна, ні непарна;

г) звертається в нуль при х = 1, т, е, arccos 1 = 0;

д)  приймає 'позитивні значення (arccos х > 0) при —1 <й
 <?х<: 1,   а  негативних  не  має;

е)  строго убуває, тобто з нерівностей — 1 < ^ < дг₂ < 1 випливає,
 що arccos x_t > arccos *₂;

ж)   найбільше значення (М = л) функція приймає при х = —1,
 а найменше (т = 0) при х — 1;

г) графік на   проміжку (— 1;0) увігнутий, а на проміжку (0;   1) — опуклий,  тому що

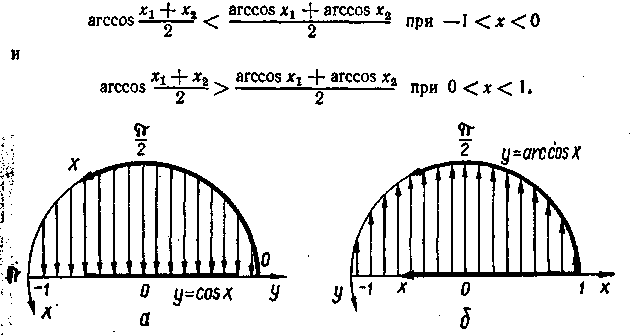
Графік функції в — arccos х приведений  на мал.   15-4. Арктангенс —   функція,  зворотна  тангенсові;  якщо те

Основні властивості функції

а) визначена при всіх дійсних значеннях х, т. е. при

б)   змінюється від тобтоі є

безперервною й обмеженою;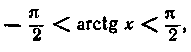

в)   непарна,  тобто

г)   звертається в нуль при х = і, тобто arctg 0 = 0;

д)   функція   приймає   позитивні   значення   (arctg х > 0)
 при 0 < х < -f- оо і негативні (arctg х < 0) при  — оо < х < 0;  '

е)   строго зростає, тобто з нерівності х± < х₂   випливає нера­
 венство arctg Xj < arctg *₂;

ж)   найбільшого і  найменшого значень не має;

з)   графік на проміжку — оо < х < 0 увігнутий,   а на проме«
 жутке  0 < х < -f- оо   опуклий,   тому   що

і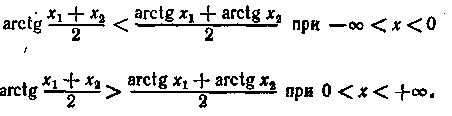

Графік функції в = arctg x приведений на мал.  15.5.

Арккотангенс — функція, зворотна котангенсові; якщо те

Основні властивості функції

а)визначена при всіх дійсних значеннях х,   тобто при

б) функція змінюється від 0 до я, тобто ПРО < arcctg х < я,   і є  безперервній  і обмеженою;

в)  задовольняє умові т.  е.  ні
 парна,   ні   непарна;

г)  у  нуль  не  звертається;

д)         приймає позитивні значення при — оо <
 < х < -+• з, а негативних не має; е) строго убуває, тобто з нера­
 венства *! < Х₂ Випливає, ЩО arcctg Xj >

> arcctg л:₂;

ж)  найбільшого і найменшого зна­
 чений  функція   не  має;

з)графіка на проміжку (— оо; 0)
 опуклий,   а на проміжку (0; -f- оо)
 увігнутий, тому що

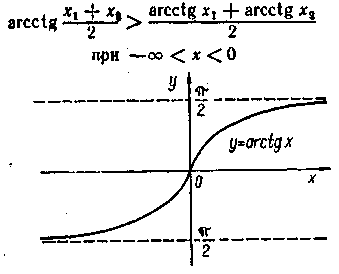
Розглянемо  приклади.

1.  Обчислити arcsin (sin 15).

Тотожність arcsin (sin х) = х можна застосувати, якщо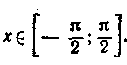

^                                                                           ^п

Визначимо, між якими кратними ~п послідовними значеннями укладене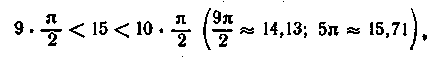 число 15. Підбором двох чисел знаходимо

або

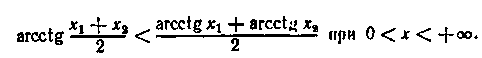
Графік функції в = arcctg я приведений  на  мал.   15.6. З визначення зворотних тригонометричних функцій   випливають такі рівності:

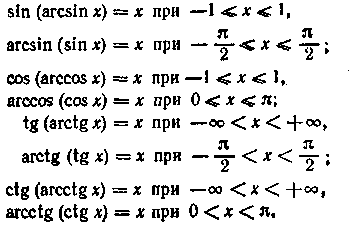
або

Отже,

Тоді

тому що

2.   Обчислити arccos (cos (— 26)).

З огляду на,  що cos (— 26) = cos 26,  визначаємо,  між  якими кратними я послідовними значеннями укладене число 26. Підбором чисел знаходимо 8я < 26 < 9я,  або 0 < 26 — 8я < я. Тоді  arccos  (cos (— 26)) = arccos (cos 26) = arccos (cos (26 — 8я))= = 26 — 8я « 0,87.

3.  Обчислити arctg (tg (— 8)).

Знайдемо, між якими послідовними кратними значеннями _li« ключено число — 8. Підбором чисел одержуємо

відкіля  випливає,   що

Оскільки tg (Зл — 8) = tg (— 8), те arctg (tg (— 8)) = arctg (tg (Зл »-— 8)) = Зл — 8 « 1,42.

4. Обчислити arcctg (ctg 16, 71).

Число 16,71 укладене між 5л і 6л, тобто 5л < 16,71   < 6л, відкіля 0 < 16,71 — 5л < я.

Тому що ctg 16,71 = ctg (16,71 — 5л),     то     arcctg   (ctg 16,71) «•

= arcctg [ctg (16,71 — 5л)1 = 16,71 — 5л « 1,00.

15.3. Співвідношення між зворотними тригонометричними функціями

Зворотні    тригонометричні   функції   можна   перетворити одна в іншу за допомогою формул

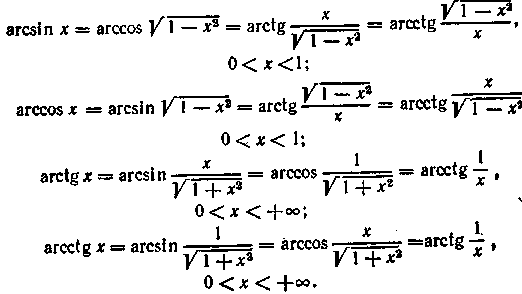
Розглянемо приклади.

/            3 \

1.   Обчислити   sin larccos -=-).

V          ⁵/

По формулі (15.6) одержуємо

Тоді

2.   Обчислити

По формулі (15.5) одержуємо

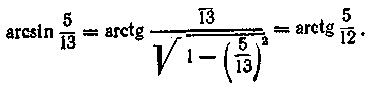
Тоді

3.   Обчислити

\                                      /

Перетворимо дане вираження, позначивши його буквою А\

По формулах (15.6) і (15.7) одержуємо

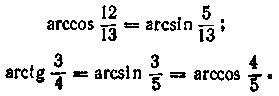
Тоді

По формулах (15.1) і (15.2) обчислюємо

Тоді,   використовуючи  формулу (14.30), по-

лучаем

Відповідно до формули (15.5)

Знаходимо

6. Довести,   що

Обчислимо

і

Тоді

Обчислимо

15.4. Формули додавання і вирахування зворотних тригонометричних функцій

Для додавання і вирахування зворотних тригонометричних функцій використовуються  наступні формули: