Зворотні кругові функції

Зворотні кругові функції. Якщо ми маємо одне рівняння з двома невідомими, то з нього, узагалі говорячи, можна визначити будь-яке невідоме через інше. Наприклад, якщо маємо: те

Перше рівняння дає вираження в у функції х. Друге, навпаки, дає вираження до у функції в. У загальному всі три рівняння виражають ту саму залежність між перемінними х и у, але тільки форма вираження цієї залежності різна перше рівняння не вирішене у наступному за функцію прийняте аргумент х, в останньому за функцію прийняте  аргумент у.

Такі дві функції, що виражають ту саму залежність між перемінними х и у) але в одній за функцію прийняте в> а в іншій за функцію прийняте х, називаються взаємно оберненими

Кожну з них можна прийняти за пряму, тоді інша буде зворотна.

Приклади взаємно зворотних функцій:

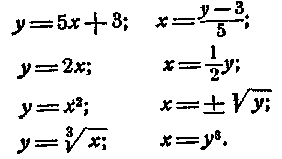
Поняття оберненості можна застосувати і до тригонометричних функцій.

Наприклад, ми вживаємо рівність.це означає, що в є синус дуги х. Очевидно, назад, х є    дуга, синус якої дорівнює в. Точно також: т. е. половина є синус дуги в 30°, Навпаки, 30° є дуга, синус якої дорівнює половині.

Замість того щоб пояснити зворотну залежність словами, вживають особливий знак, що позначає слово „дуга": Таким чином, можна написати:

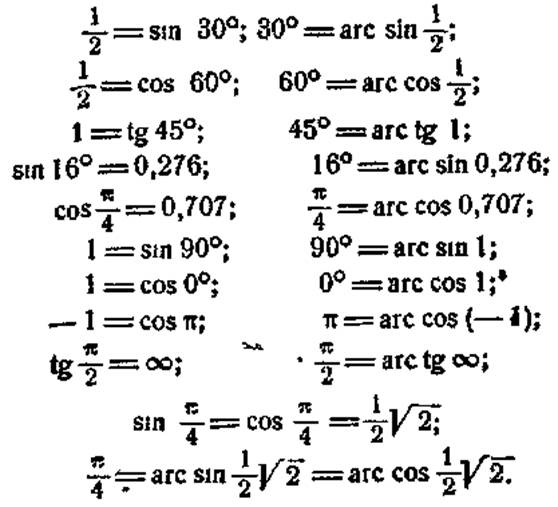
На малюнку (радіус  дорівнює одиниці)  міра  дуги  позначена через х, її синус через т, її тангенс через р. Це означає,   х  є  дуга,   синус   якої  т, а тангенс р або

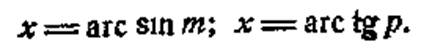
Користуючись тригонометричними таблицями, ми вирішуємо дві задачі. 1)якщо дано дугу (або кут), те ми відшукуємо тригонометричну функцію; 2)якщо дано тригонометричну функцію, то ми відшукуємо величину дуги (кута). Останнє є ніщо інше, як перебування значення оберненої тригонометричної функції за значенням її аргументу.

Ми знаємо, що однієї я тієї ж тригонометричної функції відповідає безліч дуг, що мають один і той же початокю. Наприклад, синусові, рівному

-^-, відповідають дуги п 30°, ISO⁰, 390°, 510°, . . .; основні з них, дуги в 80° і 150°, -і»еют синус, рівний вдлд> провині, «про якщо додати до кожної по 36G⁰, та і нова дуги будуть мати той же синус. Отже, .зворотні тригонометричні функції-функції" мно-"Г о. знач ны е