Педагогика \ Методика преподавания физики в средней школе

Закони збереження. Закони збереження в механіці: Плани-конспекти урокiв з фізики, страница 6

1.  Запущена під кутом до горизонту балістична ракета описала параболу й упала на поверхню Землі. Чому дорівнює робота сили тяжіння, якщо початкова і кінцева точки траєкторії лежать на одній горизонталі?

2.  Яка сила виконує роботу під час руху тіла без тертя по похилій площині?

Виклад нового матеріалу

1.     Графічне визначення роботи сталої сили. Обчислити роботу сили пружності за формулою  не можна, тому що модуль сили пружності залежить від координати (), тобто сила пружності є змінною силою.

Слід зазначити, що робота сталої сили чисельно дорівнює площі, об­меженій графіком залежності F(x) й осями координат (рис. 1).

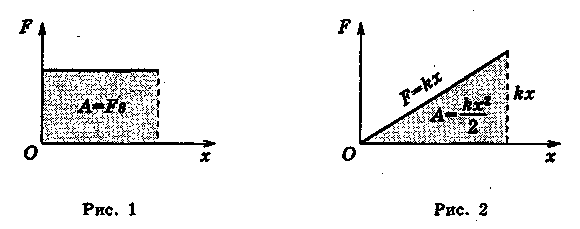
2.     Графічне визначення роботи змінної сили. Для знаходження роботи змінної сили переміщення можна розбити на малі ділянки, на кожній із яких силу можна вважати сталою. Тому й у разі змінної сили робота чисельно дорівнює площі, обмеженій графіком F(x) і осями координат. Скористаємося цим для знаходження роботи сили пружності.

Розтягуючи пружину із жорсткістю , ми прикладаємо силу , виконуючи роботу 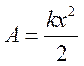, де  — величина деформації (рис. 2).

3.     Робота сили пружності. Робота сили пружності під час деформації пружини є такою самою за модулем, але від'ємною, оскільки сила пружності напрямлена протилежно деформації. Таким чином, робота сили пружності під час деформації пружини 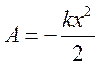. Натомість під час повернення пружини до недеформованого стану сила пружності виконує додатну роботу .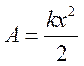

Так само, як і для роботи сили тяжіння, обидва вирази для роботи сили пружності можна подати однією формулою. У результаті дістане­мо, що робота сили пружності

,

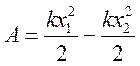де  і  — величини початкової та кінцевої деформації пружини від­повідно.

Слід зазначити, що робота сили пружності (так само, як і робота сили тяжіння) дорівнює нулю в разі переміщення тіла по замкнутій тра­єкторії.

Таким чином, можна зробити висновки.

Робота сили пружності аналогічна роботі сили тяжіння і залежить лише від деформації пружини в початковому та кінцевому станах.

У разі переміщення тіла по замкнутій траєкторії робота сили пружності дорівнює нулю.

Питання до учнів у ході викладу нового матеріалу

1.  Чому не можна застосувати загальну формулу роботи для обчислення роботи сили пружності?

2.  Яку роботу — додатну чи від'ємну — виконує сила пружності під час стиснення пружини? Під час повернення пружини до недеформованого стану?

3.  У чому подібність робіт, виконуваних силою тяжіння і силою пружності?

Задачі, розв'язувані на уроці

1.  До пружини, довжина якої в недеформованому стані 0,2 м, підвісили тягар масою 30 кг. Жорсткість пружини 10 кН/м. Чому дорівнює довжина деформованої пружини?

2.  Під дією сили 5 Н пружина розтяглася на 2 см. Яку роботу виконує зовнішня сила під час розтягнення цієї пружини на 5 см?

3.  Динамометр, розрахований на 40 Н, має пружину жорсткістю 500 Н/м, Яку роботу потрібно виконати, щоб розтягти пружину від середини шкали до останньої поділки?

Домашнє завдання

Основне:

1.  К: § 47, впр. 28 (1, 2, 4, 6).

2.  Г: § 21 (21.3).
Додаткове:

1. Ф-9: § 53.

2. К: впр. 28 (7, 8).

УРОК 7/62. РОБОТА СИЛИ ТЕРТЯ

Мета уроку:  з'ясувати особливості роботи сили тертя.

Тип уроку:  комбінований урок.

Демонстрації:  робота сили тертя під час руху бруска.

План викладу нового матеріалу:1. Напрям сили тертя.

2.  Робота сили тертя.

3. Особливості роботи сили тертя.

Перевірка знань

1.  Як обчислити роботу сили тяжіння?

2.  Як обчислити роботу сили пружності?

3.  Доведіть, що робота сили пружності на замкнутій траєкторії дорівнює нулю.

Виклад нового матеріалу

На початку уроку слід підкреслити, що сила тертя ковзання не зале­жить від координати, а залежить від відносної швидкості дотичних тіл і завжди напрямлена в бік, протилежний відносній швидкості дотичних тіл. Під час ковзання тіла по нерухомій поверхні кут між напрямом пере­міщення і напрямом сили тертя дорівнює 180°. Оскільки , то рсібота сили тертя ковзання завжди є величиною від'ємною, тобто .

Отже, робота сили тертя ковзання на будь-якій ділянці траєкторії є від'ємною (у системі відліку, зв'язаній із тілом, по якому ковзає дане тіло). Те саме стосується і сил опору під час руху в рідині або газі.

Звідси випливає важливий висновок: робота сили тертя ковзання під час переміщення по замкнутій траєкторії є завжди від'ємною й, от­же, відмінною від нуля. Ця властивість сили тертя суттєво відрізняє її від сили тяжіння і сили пружності.

Питання до учнів у ході викладу нового матеріалу

1.  Від чого залежить значення сили тертя ковзання?

2.  Чи залежить сила тертя від координат?

3.  Чи залежить сила тертя від форми траєкторії?

4.  Чим суттєво відрізняється робота сили тертя від роботи сили тяжіння і сили пружності?

Задачі, розв'язувані на уроці

1.    Хлопчик тягне горизонтальною дорогою санки, прикладаючи до них силу = 50 Н, напрямлену під кутом = 45° до горизонту. Яку роботу виконав хлопчик, пройшовши  = 1 км? Яку роботу виконала на цьому шляху сила тертя, що діяла на санки, якщо санки руха­лися рівномірно? (36: № 24.7)

Розв'язання. Робота, яку виконав хлопчик, . Санки ру­халися рівномірно, тому сила тертя за модулем дорівнювала проекції сили Fна горизонтальну вісь . Отже, робота сили тертя відріз­няється від роботи, виконаної хлопчиком, тільки знаком:.

2.    Санки з хлопчиком, скотившись із гори, рухалися по горизонтальній поверхні до зупинки протягом 10 с. Знайдіть роботу сили тертя на шляху гальмування, якщо маса хлопчика і санок 50 кг, а коефіцієнт тертя санок об сніг дорівнює 0,02.

Розв'язання. У формулу роботи сили тертя  потрібно підставити вираз для сили тертя () і для пройденого шляху .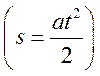

Тоді .

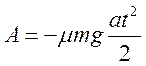Модуль прискорення можна знайти за другим законом Ньютона:

.

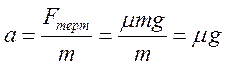Отже,

.

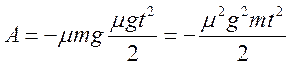3.  Поїзд, маса якого 4000 т, рушає з місця і рухається з прискоренням 0,2 м/с2 протягом 1,5 хв. Знайдіть роботу локомотива під час розгону, якщо коефіцієнт опору рухові дорівнює 0,05. (Відповідь: 2,3 мДж.)

Скачать файл