Закони збереження. Закони збереження в механіці: Плани-конспекти урокiв з фізики, страница 14

Задача. У брусок, що висить на шнурі довжиною  = 2м, влучила ку­ля зі стрілецької зброї, яка летіла горизонтально. Куля застрягла в бруску. З якою швидкістю летіла куля, якщо шнур відхилив­ся від вертикалі на кут  = 15°? Маса бруска = 2 кг, маса кулі = 8 г.

Дано:                                                        Розв'язання

= 2 м                               Процес можна разбити на два етапи. Пер-

= 12°                              ший етап — зіткнення кулі з бруском. При

 = 2 кг                          цьому брусок набирає швидкість , але

= 8 г = 0,008 кг            практично не встигає зрушити з місця. Ме-

 – ?  ханічна енергія не зберігається, але зберігається імпульс: . На другому етапі процесу брусок із за­стряглою в ньому кулею відхиляється на кут , підіймаючись при цьому (див. рисунок) на висоту .

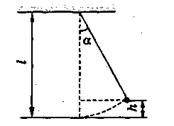
Ha цьому етапі механічна енергія зберігається:

Звідси

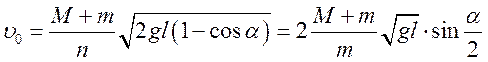
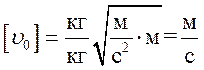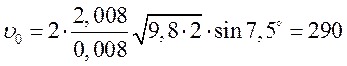,  (м/с).

Відповідь:  = 290 м/с.

Особливу увагу учнів необхідно привернути до розв'язування задач на пружне зіткнення. Пружним зіткненням (ударом) називають таке зіткнення тіл, коли зберігається механічна енергія. Таким чином, у про­цесі розв'язування задач на пружні зіткнення можна користуватися за­коном збереження імпульсу і законом збереження енергії (нагадаємо, що в разі непружних зіткнень можна користуватися тільки законом збере­ження імпульсу).

Задача. Дві кулі (тіла круглої форми) однакової маси рухаються вздовж однієї прямої зі швидкостями  і Якими будуть швидкості куль  і  після зіткнення?

Розв'язання. Позначимо масу кажної з куль . Згідно із заковом збе­реження імпульсу,  а згідно із законом збереження енергії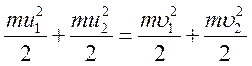 . Напрямимо вісь х уздовж лінії руху куль. Тоді у проекціях на вісь х закони збереження імпульсу та енергії записуються у вигляді

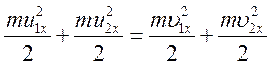
Обидва рівняння можна скоротити на , а друге рівняння, крім того, помножити на 2, після чого ми дістанемо два рівняння з двома невідо­мими і :

,

Перегрупуємо доданки в цих рівняннях так, щоб усі величини, які стосуються першої кулі, були ліворуч від знака рівності, а всі величи­ни, які стосуються другої кулі,— праворуч:

,                                       (1)

                                        (2)

Оскільки в умові сказано, що зіткнення відбулося, швидкості куль змінилися, тобто , , тому обидві частини першого рів­няння відмінні від нуля й, отже, друге рівняння можна почленно розді­лити на перше. У результаті дістанемо . Розв'язуючи це рівняння разом із рівнянням (1), одержуємо , . Це означає, що в результаті пружного зіткнення кулі однакової маси об­мінюються швидкостями.

Непружним ударом називають таке зіткнення тіл, коли тіла після зіткнення рухаються з однаковими (за модулем і за напрямом) швидко­стями. Іноді після зіткнення тіла рухаються як єдине ціле,— наприклад, куля застряє в бруску. Часто в умові задач дано маси та швидкості тіл, що стикаються, а потрібно знайти кінцеву швидкість єдиного тіла, яке утворилося. Позначимо маси тіл, що стикаються, і , а їхні почат­кові швидкості  і .

Після зіткнення тіла будуть рухатися як одне тіло з масою . Позначимо кінцеву швидкість цього тіла п. Тоді, згідно із законом збе­реження імпульсу, . Звідси одержуємо

.

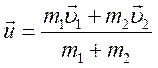Задача. Куля масою = 10 г , яка вилетіла зі стрілецької зброї й летить горизонтально, влучає в брусок масою = 1 кг, що лежить на столі, й застряє в ньому. З якою швидкістю буде рухатися після цього бру­сок із кулею, якщо швидкість кулі дорівнює 100 м/с? Розв'язання. Розглядаючи зіткнення кулі з бруском, можна користу­ватися законом збереження імпульсу. Позначимо модуль швидкості

кулі v, а модуль швидкості бруска з кулею безпосередньо після влучен­ня кулі v. Оберемо вісь х у напрямі руху кулі, тоді проекції обох швид­костей є додатними й дорівнюють модулям швидкостей. Тому закон збереження імпульсу можна записати у вигляді: . Звідси 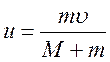. Підставляючи числові дані, одержуємо  = 0,99 м/с. Задачі, розв'язувані на уроці

1.   Куля (тіло круглої форми) масою т налітає на нерухому кулю масою . Після пружного зіткнення напрям швидкості першої кулі утворює кут 30° із напрямом її початкової швидкості. З якими швидкостями рухаються кулі після зіткнення, якщо початкова швидкість першої кулі ? (Відповідь: перша куля рухається зі швидкістю , друга — зі швидкістю  під кутом 30° до початкової швидкості першої кулі.)

2.   Для автоматичного перезарядження гармати використовують енергію віддачі: відкотні частини гармати мають переміститися після пострілу на х = 50 см, стискаючи пружину жорсткістю = 40 кН/м. Якою є початкова швидкість  снаряда масою = 2,5 кг, якщо маса відкотних частин гармати = 150 кг? Вважайте положення дула горизонтальним.

Розв'язання. Процес складається з двох етапів: 1-й етап — швидке згоряння пороху, в результаті якого і снаряд, і відкотні частини набува­ють однакових за модулем імпульсів (швидкість відкотніх частин 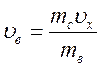), 2-й етап — перехід кінетичної енергії відкотних частин у потенціальну енергію пружно деформованої пружини 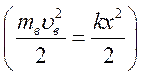. Звідси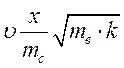

Відповідь: 490 м/с.

3.   Підвішена на нитці кулька здійснює коливання. Коли кулька проходить положення рівноваги, сила натягу нитки у 2 рази перевищує силу тяжіння, що діє на кульку. На який максимальний кут  від вертикалі відхиляється нитка?

Розв'язання. Згідно з умовою вага кульки в нижній точці у 2 рази пе­ревищує силу тяжіння, що діє на кульку. Отже, нормальне прискорення кульки в цій точці за модулем дорівнює , звідки .

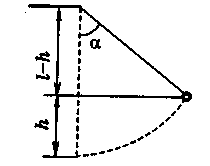
У момент максимального відхилення від положення рівноваги вся кінетична енергія кульки  переходить у потенціальну , звідки . Як видно з рисунка , Отже,

Відповідь:  = 60°.

Домашнє завдання

Основне:

1.  К:впр. 30 (7, 8, 9).

2.  Г: § 24 (24.3).

3.  1)  Куля з пневматичної гвинтівки, що летить горизонтально зі швидкістю 50 м/с, влучає в брусок, який лежить на столі, й застряє в ньому. На яку відстань переміститься брусок, якщо його маса в 49 разів більша від маси кулі, а коефіцієнт тертя між бруском і столом дорівнює 0,2? (36: № 27.3)