Закони збереження. Закони збереження в механіці: Плани-конспекти урокiв з фізики, страница 19

3.  Куля (тіло круглої форми) масою 400 г налітає на нерухому кулю масою 200 г. Після пружного зіткнення напрям швидкості першої кулі утворює кут 30° із напрямом її початкової швидкості. З якими швидкостями рухаються кулі після зіткнення, якщо початкова швидкість першої кулі 5 м/с?

4. Невелике тіло зісковзує з вершини півсфери радіусом 30 см. На які: висоті тіло .зірветься з поверхні півсфери й полетить униз? Тертя не враховувати.

Варіант 2

1.  За рахунок якої енергії злітає вгору наповнена гелієм повітряна кулька, що вирвалася з рук?

2.  Куля масою 20 г, випущена зі стрілецької зброї під кутом а до горизонту, у верхній точці траєкторії має кінетичну енергію 88,2 Дж Знайдіть кут а, якщо початкова швидкість кулі 600 м/с.

3.  Мавпа гойдалася на тонкій довгій ліані, причому максимальний кут відхилення ліани від вертикального положення дорівнював 60° Коли мавпа була в нижній точці, ліана зачепилася серединок за гілку. На який кут від вертикалі відхилиться тепер нижня частина ліани?

4.  Предмет масою т обертається на нитці у вертикальній площині. На скільки сила натягу нитки в нижній точці є більшою, ніж у верхній?

УРОК 19/74. ТИСК У РУХОМИХ РІДИНАХ І ГАЗАХ

Мета уроку: пояснити закони Паскаля і Бернуллі; навчити учнів за­стосовувати закон збереження енергії до руху рідин і газів у трубах.

Тип уроку: урок вивчення нового матеріалу.

Демонстрації:   1. Залежність тиску рідини від швидкості її протікання.

2. Будова і принцип дії пульверизатора та водоструменевого насосу.

Плай викладу нового матеріалу:1. «Ідеальна рідина».

2.  Закон Паскаля.

3.  Гідростатичний тиск.

4.  Рівняння Бернуллі.

5.  Закон Бернуллі.

Перед початком вивчення нової теми необхідно проаналізувати резуль­тати тематичного оцінювання з теми «Закони збереження в механіці». Для цього можна скористатися методичними рекомендаціями, поданими до уроку № 17/17 (с. 87).

Виклад нового матеріалу

1.     «Ідеальна рідина». На початку викладу нового матеріалу слід познайомити учнів із поняттям «ідеальної рідини». Під ідеальною рідиною ми будемо розуміти рідину, для якої виконуються такі умови:

•  рідина вважається, нестисливою;

•  тертям між її шарами, а також між рідиною і стінками посудини можна знехтувати.

«Заміна» реальної рідини ідеальною є припустимою, якщо швидкість руху рідини досить мала.

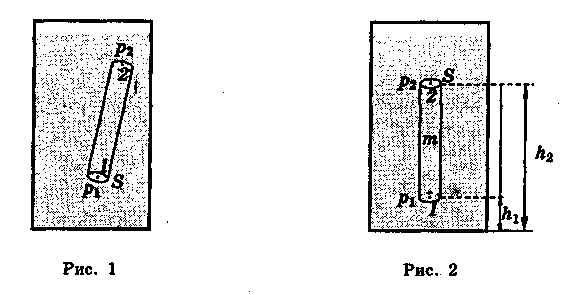
2.     Закон Паскаля. Виведемо закон Паскаля, скориставшись першою умовою рівноваги. Виділимо подумки циліндричний об'єм рідини, основи якого розташовані в довільних точках 1 і 2 (рис. 1). Оскільки сили тиску рідини на бічну поверхню циліндра взаємно компенсуються, мають компенсуватися і напрямлені протилежно, сили тиску на основи циліндра: , де  — площа основи циліндра. Звідси випливає .

Оскільки точки 1 і 2 були обрані довільно, одержуємо: , що й відповідає формулюванню закону Паскаля: якщо знехтувати вагою рідини, тиск у всіх точках нерухомої рідини є однаковим.

3.     Гідростатичний тиск. Задамо положення точки в рідині висотою цієї точки відносно дна посудини, поверхні землі або будь-якого іншого горизонтального рівня.

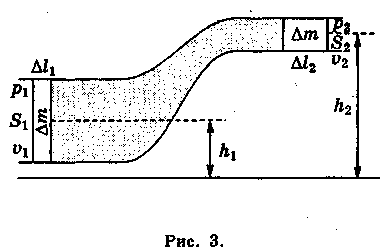
Розглянемо умову рівноваги виділеного вертикального циліндричного об'єму рідини (рис. 2).

Якщо необхідно враховувати вагу рідини, то, крім сил тиску, що діють на основи циліндра, слід урахувати й силу тяжіння , що діє на ци­ліндр, де — маса рідини, що міститься в циліндрі. Об'єм циліндра , тому , де  — густина рідини.

Таким чином, умова рівноваги виділеного об'єму рідини набуває ви­гляду , звідки . Оскільки точ­ки 1 і 2 обрані довільно, ми бачимо, що для всіх точок рідини величина є однаковою.

Отже, якщо необхідно враховувати вагу рідини, то:

.

де  — висота точки, — тиск у цій точці.

Із цієї формули випливає, що чим нижче розташована точка, тобто чим менша висота , тим більшим є тиск у цій точці. Це збільшення тиску зумовлене вагою розташованих вище шарів рідини: шар рідини висотою  створює тиск . Цей тиск називається гідростатичним тиском.

Необхідно привернути увагу учнів до того, що формула  не «перекреслює» закон Паскаля, а узагальнює його. Дійсно, якщо вагою рідини можна знехтувати, тобто , ця формула зводиться до р = const', тобто до закону Паскаля.

4. Рівняння Бернуллі. Для обчислення тиску в рухомій рідині скори­стаємося законом збереження енергії. Якщо енергія виділеного об'єму рідини змінюється, це означає, що сили тиску виконують роботу над цим об'ємом рідини: , де  — зміна енергії виділеного об'єму ріди­ни,  — робота сил тиску.

Таким чином, нам потрібно знайти вирази для  і і дорівняти їх один до одного.

Під час руху рідини можуть змінюватися висота, на якій розташований певний елемент рідини, і швидкість протікання, тобто може змінювати­ся і потенціальна, і кінетична енергія певного елемента рідини.

Тиск, швидкість протікання і висоту в перерізі 1 позначимо, відповід­но, , , і , а площу перерізу . Аналогічно позначимо відповідні величини в перерізі 2 (рис. 3).

Роботу, виконану силами тиску над виділеним об'ємом рідини, мож­на записати у вигляді . Оскільки рідина нестислива, об'єми і є однаковими. Кожний із них дорівнює , тому

Зміна енергії цього об'єму може бути зумовлена зміною як висоти (зміна потенціальної енергії), так і швидкості протікання (зміна кіне­тичної енергії). Ураховуючи обидві можливі причини зміни енергії,

одержуємо: 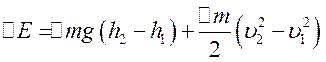. Дорівнюючи вирази для  і  і скорочуючи обидві частини рівності на , дістанемо:

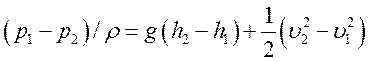
Помножимо обидві частини одержаної рівності на р і перенесемо потім усі величини, що стосуються перерізу 1, ліворуч, а ті, що стосу­ються перерізу 2,— праворуч. У результаті дістанемо:

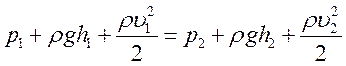
Оскільки перерізи 1 і 2 обрані довільно, ми бачимо, що для всіх точок рідини величина 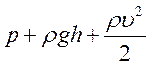 є однаковою. Таким чином, в одному й тому самому потоці рідини (або газу)

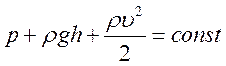
Це рівняння вперше було виведене Д. Бернуллі й називається тому рів­нянням Бернуллі.