Закони збереження. Закони збереження в механіці: Плани-конспекти урокiв з фізики, страница 13

Розв'язання. На м'яч під час польоту діє тільки сила тяжіння, тому

механічна енергія м'яча зберігається. Отж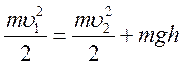е, , де  —маса м'яча,  — його початкова швидкість,  — швидкість м'яча на висоті . Звідси . Підставляючи числові дані, одержуємо =24 м/с.

2.   На нитці довжиною підвішено кульку масою то. Кульку відхиляють так, що нитка стає горизонтальною, і відпускають. З якою швидкістю кулька пройде положення рівноваги? Якою буде при цьому сила натягу нитки ?

Розв'язання. На кульку під час її руху діють тільки сила тяжіння і сила пружності, тому механічна енергія кульки зберігається. Зістави­мо нульовой рівень потенціальної енергії зі станом системи, коли кулька перебуває в найнижчому положенні. Тоді, якщо нитка відхилена на 90°,

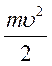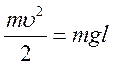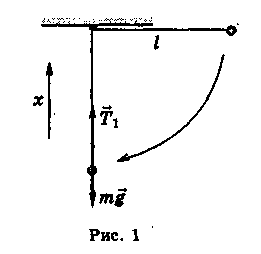
потенціальна енергія кульки дорівнює . У нижній точці потенціаль­на енергія кульки дорівнює нулю, а кінетична енергія дорівнює . Відповідно до закону збереження енергії, . Звідси . Слід звернути увагу: швидкість кульки виявилася за модулем такою са­мою, якою була б у випадку, якби кулька вільно падала з висоти . Знайдемо тепер силу натягу нитки в нижній точці (рис. 1).

На кульку діють дві сили: сила тяжіння і сила реакції нитки , напрямлені протилежно. Оскільки кулька рухається по колу радіуса , рівнодійна цих сил надає кульці доцентрове прискорення, що дорів­нює .

У проекціях на напрямлену вгору вісь х рівняння другого закона Ньюто­на має вигляд 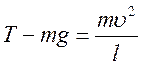- . Праву частину цього рівняння легко знайти, скориставшись законом збереження енергії: з 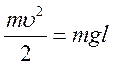 випливає, що 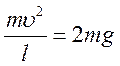. Звідси , тобто . Таким чином, під час проходження положення рівноваги сила натягу нитки є втричі більшою, ніж сила тяжіння.

3. Невелике тіло масою зісковзує без тертя по похилому жолобу, що переходить у коло радіусом , і проходить «мертву петлю», не від­риваючись від жолоба. З якою силою  тисне тіло на жолоб у верхній точці кола, якщо тіло зісковзує з висоти ? 3 якої мінімальної по­чаткової висоти має зісковзувати тіло, щоб воно під час руху не відривалося від жолоба (рис. 2)?

Розв'язання. Якщо тіло у верхній точці не відривається від жолоба, на тіло в цій точці діють сила тяжіння і сила реакції жолоба , обидві напрямлені вниз. Оскільки тіло рухається по колу радіусом , рівнодійна цих сил надає тілу доцентрового прискорення , де — швидкість тіла у верхній точці кола.

У проекціях на напрямлену вниз вісь х рівняння другого закону Нью­тона має вигляд 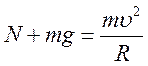. Щоб знайти праву частину цього рівняння, можна скористатися законом збереження механічної енергії, оскільки на тіло під час його руху діють тільки сила тяжіння і сила пружності. Зіставимо нульовий рівень потенціальної енергії зі ста­ном, коли тіло перебуває в нижній точці кола. Тоді 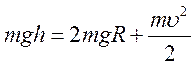, звідси .

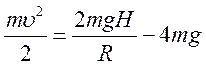Підставляючи одержаний вираз для 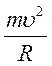 у рівняння ,

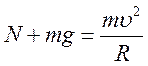знаходимо 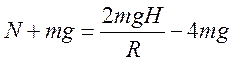, звідки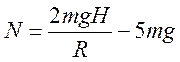

Оскільки , одержуєм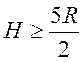о , тобто .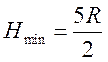

4.   Автомобіль масою = 1 т збільшує швидкість від = 5 м/с до =15 м/с. Накресліть графік залежності його швидкості від часу, вважаючи корисну потужність двигуна сталою ( = 10 кВт) і нехтуючи силами опору. (36: № 25.29)

Розв'язання. Автомобільний двигун за час виконав роботу . За теоремою про кінетичну енергію ця робота дорівнює зміні кінетич­ної енергії 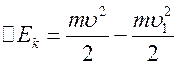, де — швидкість автомобіля в момент

часу . Звідси одержуємо формулу 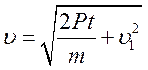 (рис. 3).

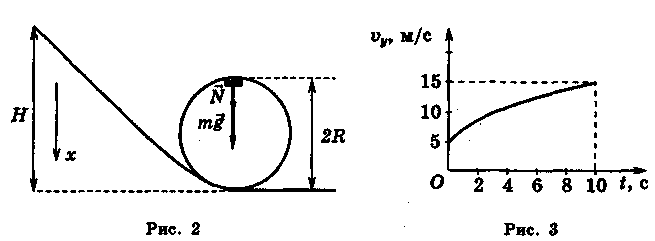
5.   Пружинний пістолет стріляє кульками вертикально вгору. Маса кульки 2,25 г. На яку висоту пістолет закине кульку, якщо жорсткість пружини 90 Н/м, а деформація пружини 3 см? З якою швидкістю кулька вилітає з пістолета? Масою пружини та опором повітря знехтувати.

Домашнє завдання

Основне:

1.  К: впр. ЗО (1, 2, 4, 5).

2.  Г:§ 24 (24.1, 24.2).

3.  1)  Кокосовий горіх масою 8 кг падає з висоти 8 м. Знайдіть його кінетичну і потенціальну енергії через 1 с. На якій висоті ці енергії є однаковими? (36: № 25.20)

2)  3 якою швидкістю кинули баскетбольний м'яч, якщо він пролетів через кільце зі швидкістю 3 м/с? Кидок зроблено з висоти 2 м, кільце розташоване на висоті 3 м. (36: № 25.21)

3)  Тіло кинуто зі швидкістю  під кутом а до горизонту. Користуючись законом збереження енергії, знайдіть: а) висоту  верхньої точки траєкторії та швидкість тіла в цій точці; б) модуль і напрям швидкості тіла на висоті . (36: № 25.23)

4)   Тіло масою 2 кг кинули під кутом до горизонту. У верхній точці траєкторії на висоті 20 м його кінетична енергія дорівнює 100 Дж. Якою була початкова швидкість тіла? Під яким кутом до горизонту його кинули? (36: № 25.24) Додаткове:

1.  Ф-9: § 59.

2.  36: №25.30.

УРОК 15/70. ЗАСТОСУВАННЯ ЗАКОНІВ ЗБЕРЕЖЕННЯ ЕНЕРГІЇ ТА ІМПУЛЬСУ

Мета уроку: розширити уявлення учнів про сферу використання законів збереження енергії та імпульсу; навчити їх застосовувати свої знання для розв'язування відповідних задач. Тип уроку: урок закріплення знань.

Рекомендації щодо розв'язування задач

Засвоєнню теоретичного матеріалу про використання законів збе­реження енергії й імпульсу сприяють правильно організовані заняття з розв'язування задач.

Структурним принципом усього курсу механіки середньої школи є роз­в'язання основної задачі механіки, бо саме ця задача визначає зміст і структуру всієї сукупності необхідних понять. Динамічний спосіб роз­в'язання основної задачі механіки вимагає знання сил, що діють на тіло в будь-який момент часу. Коли відбуваються реальні взаємодії, значення цих сил відомі далеко не завжди. У таких випадках застосовується енер­гетичний спосіб розв'язання. Крім того, енергетичний спосіб часто дає більш раціональне розв'язання і в тих випадках, коли можливим є засто­сування динамічного способу розв'язання основної задачі механіки. Низку задач можна розв'язати тільки в результаті застосування обох за­конів збереження (імпульсу й енергії).