Исследование нелинейных систем автоматического управления методом фазовых траекторий

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Сибирский государственный технологический университет

Факультет автоматизации и информационных технологий

Кафедра автоматизации производственных процессов

Исследование нелинейных систем автоматического управления

методом фазовых траекторий

Пояснительная записка

(ПМ.000000.000.ПЗ)

Руководитель:

_____________Чмых Г.И.

           ^{(подпись)}

_____________________________

              ^{(оценка, дата)}

Выполнил:

Студент группы 23-1

_____________Миронов К.А.

           ^{(подпись)}

_____________________________

                        ^(дата)

Красноярск 2005

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Сибирский государственный технологический университет

Факультет автоматизации и информационных технологий

ЗАДАНИЕ

к расчетно-графической работе

Тема: «Исследование нелинейных систем автоматического управления методом фазовых траекторий»

Студент: Миронов К.А. гр. 23-1

Дата выдачи:                       2005 г.

Срок выполнения:              2005 г.

Руководитель: Чмых Г.И.

Задание

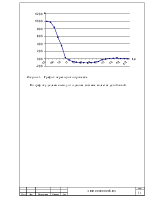
1 Построить фазовый портрет системы при различных начальных условиях.

2 Построить график переходного процесса во времени для одной из фазовых траекторий.

3 Дать оценку устойчивости системы.

Исходные данные:

Передаточная функция линейной части:

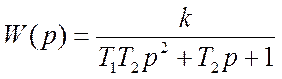
  Таблица 1 –  Параметры линейной и нелинейной частей САР

k	T1	T2	c	b
0.45	0.4	0.65	2.5	3.5

Графический материал представлен двумя рисунками:

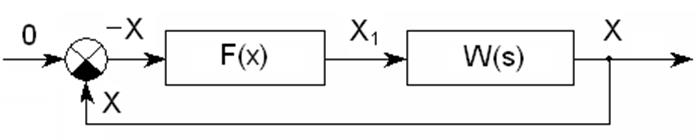
  Рисунок 1 –  Структурная схема системы автоматического регулирования

 

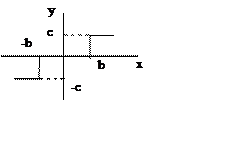  Рисунок 2 –  Статическая характеристики нелинейного элемента

Руководитель:

______________________________

       ^{(подпись)}

Задание принял к исполнению:

______________________________

       ^{(подпись)}

Содержание

1 Расчет и вывод необходимых значений и выражений………………………..5

2 Построение фазового портрета методом изоклин…………………………….7

3 Построение переходного процесса …………………………………………....9

Заключениие ……….…………………………………………………...……….16

Список использованных источников ………………………………..…………17

1 Расчет и вывод необходимых значений и выражений

Исходя из рисунка 1, находим:

                             ,                     (1)

Подставляем в (1) известные данные:

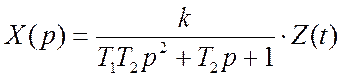                                  ,  (2)

                               .    (3)

Переходим к дифференциальным уравнениям:

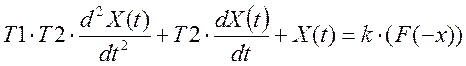                       ,                                                                 (4)

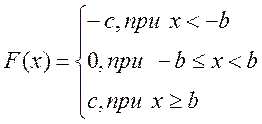где .                                         (5)

Учитывая, что , перейдём к нормальной форме Коши:

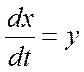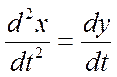                                           , .          (6)

С учетом формулы (6):

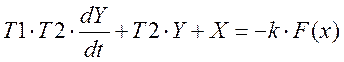                                     (7)

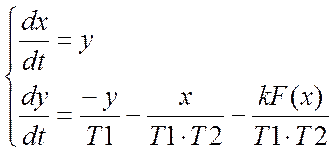                                  ,   (8)

Найдем дифференциальное уравнение фазовой траектории для этого разделим нижнее уравнение системы (8) на верхнее:

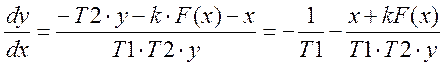                                                                                            (9)

Сделаем замену 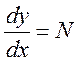 в (9),

где ,

 – угол наклона фазовых траекторий и выразим y,

получим

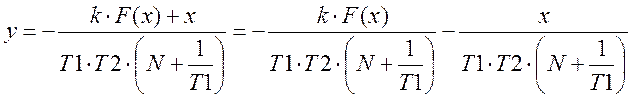                                                                (10)

Выражение (10) есть ничто иное, как уравнение изоклины.

2 Построение фазового портрета методом изоклин

Построение изоклин ведем следующим методом.

Вычисляем угол наклона фазовой траектории при прохождении ее через изоклину, в зависимости от угла наклона самой изоклины.

                                                                 (11)

Общее уравнение прямой имеет вид .      (12)

Из выражений (10) и (11) ,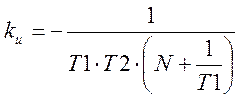

где – коэффициент наклона изоклины.

Откуда

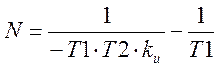                                           .         (13)

                                                   ,                 (12)

где ­– угол наклона изоклины относительно горизонтальной оси.

Задавая значения угланайдем значения . Результат и предварительные результаты поместим в таблицу 2.

  Таблица 2 –  Результаты расчета углов