Линейная часть нелинейной системы состоит из двигателя постоянного тока и безынерционного усилителя. Передаточная функция линейной части:
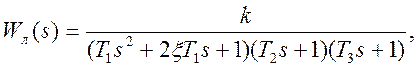 (1)
(1)
где Т1 – электромеханическая постоянная времени двигателя, с;
Т2 – электромагнитная постоянная времени двигателя, с;
Т3 - электромагнитная постоянная времени двигателя, с;
k – общий коэффициент усиления линейной части, с-1 .
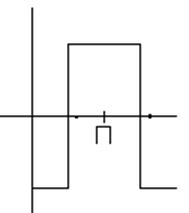
Нелинейный элемент – реле с гистерезисом.
Статическая характеристика нелинейного элемента:
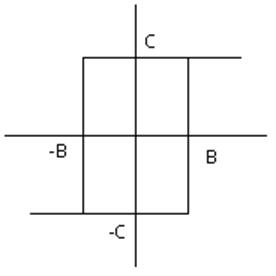
Рисунок 1.
Если
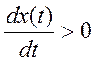 , то
, то 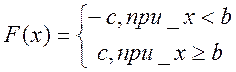 (3)
(3)
Если 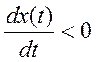 , то
, то 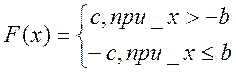 (4)
(4)
Рисунок 1- Статическая характеристика реле
Значения параметров: Т1 = 0,04; Т2= 0,8 ; Т2 = 1; k=2,5 ;ζ = 0,5; b=4; c=6.
Определить:
- возможность автоколебаний и их устойчивость;
- частоту и амплитуду автоколебаний при наличии периодического режима в системе.
Решение
1) Определяем комплексную частотную передаточную функцию, подставив в (4) s=jω:
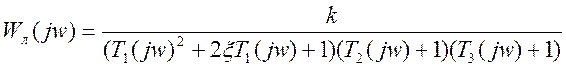 .
(4)
.
(4)
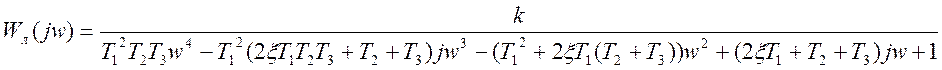
2) Выделяем мнимую и вещественную части Wл(s):
![]()
где
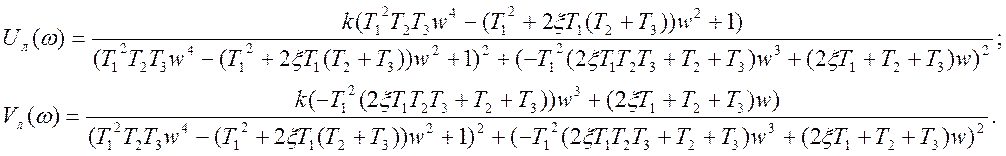
3) После подстановки в (5) численных значений параметров звеньев получим:
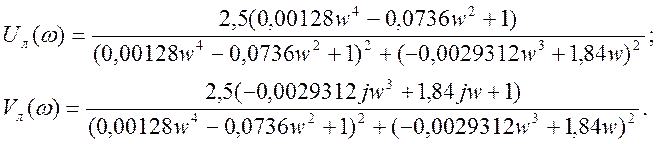 (5)
(5)
4) Изменяя частоту ω, рассчитываем значения Uл(ω) и Vл(ω).
|
w |
U |
V |
|
0 |
2,5 |
0 |
|
1 |
0,547574 |
1,084350718 |
|
2 |
0,130613 |
0,657768746 |
|
3 |
0,037023 |
0,456483638 |
|
4 |
0,00729 |
0,348405661 |
|
5 |
-0,001281 |
0,283004521 |
|
6 |
0,000214 |
0,240225949 |
|
7 |
0,008265 |
0,210208481 |
|
8 |
0,021633 |
0,18661057 |
|
9 |
0,03908 |
0,164021164 |
|
10 |
0,057345 |
0,137741707 |
|
20 |
0,014095 |
0,001066971 |
|
30 |
0,002572 |
-6,33731E-05 |
|
40 |
0,00079 |
-2,85025E-05 |
|
50 |
0,000319 |
-1,12127E-05 |
|
60 |
0,000153 |
-4,89871E-06 |
|
70 |
8,22E-05 |
-2,37356E-06 |
|
80 |
4,81E-05 |
-1,25259E-06 |
|
90 |
3E-05 |
-7,08362E-07 |
|
100 |
1,96E-05 |
-4,23848E-07 |
5) По результатам расчета строим АФЧХ линейной части (рисунок 2).
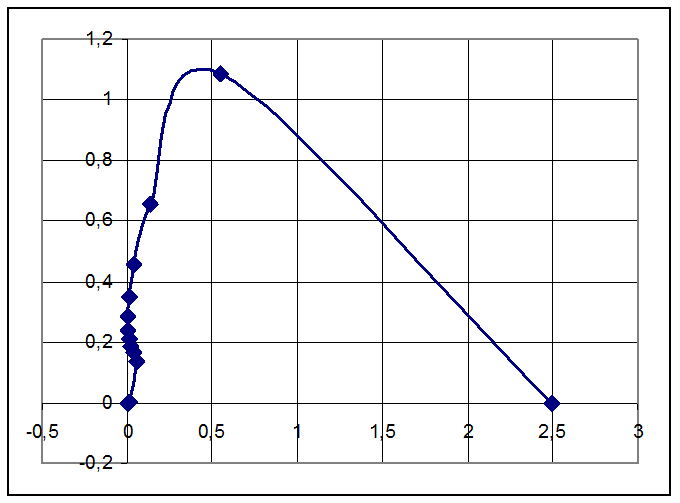
Как видно из рисунка, АФЧХ охватывает точку с координатами –1,j0. Делаем заключение, что замкнутая система без учета нелинейности будет неустойчивой.
6) Коэффициенты гармонической линеаризации для релейного элемента с гистерезисом находятся по следующим формулам:
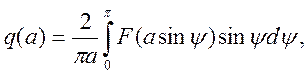
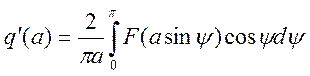 .
.
Интегрируем на полу периоде из-за того, что релейный элемент с гистерезисом описывается следующей ступенчатой функцией:
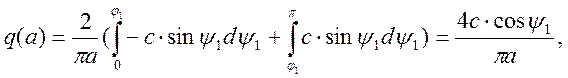 (6)
(6)
![]()
![]() ,
,
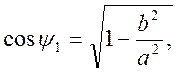
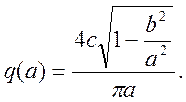 (7)
(7)
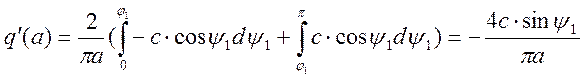 ,
(8)
,
(8)
![]()
 (9)
(9)
7) Амплитудно-фазовая характеристика гармонически линеаризованного нелинейного элемента:
![]()
![]()
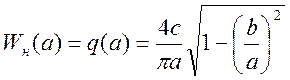 . (10)
. (10)
8) Инверсная отрицательная амплитудно-фазовая характеристика нелинейного элемента:
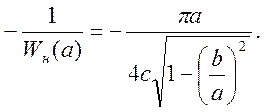 (11)
(11)
9)Подставляем в (9) численные значения:
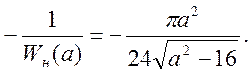 (12)
(12)
На рисунке 3 приведены графики
функций ![]() и
и 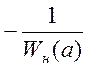 ,
рассчитанные при различных значениях а
,
рассчитанные при различных значениях а![]() .
Из рисунка видно, что функции имеют экстремум при
.
Из рисунка видно, что функции имеют экстремум при ![]() .
.
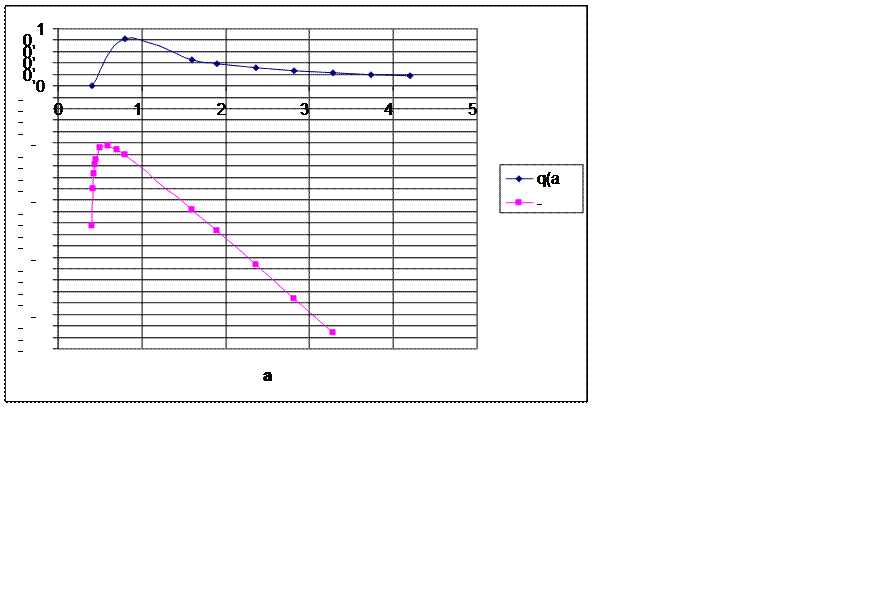
Рисунок 3 – Линеаризованная амплитудно-фазовая и отрицательная инверсная амплитудно-фазовой характеристики поляризованного реле с зоной нечувствительности
10) Строим инверсную характеристику 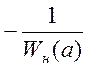 на комплексной плоскости (рисунок 4).
на комплексной плоскости (рисунок 4).
Эта характеристика представляет прямую, расположенную на вещественной отрицательной полуоси, поскольку мнимая часть выражения (10) равна нулю. Характеристика имеет две совпадающие точки пересечения с АФЧХ линейной части, так как она изменяет направление движения при а = 0,82
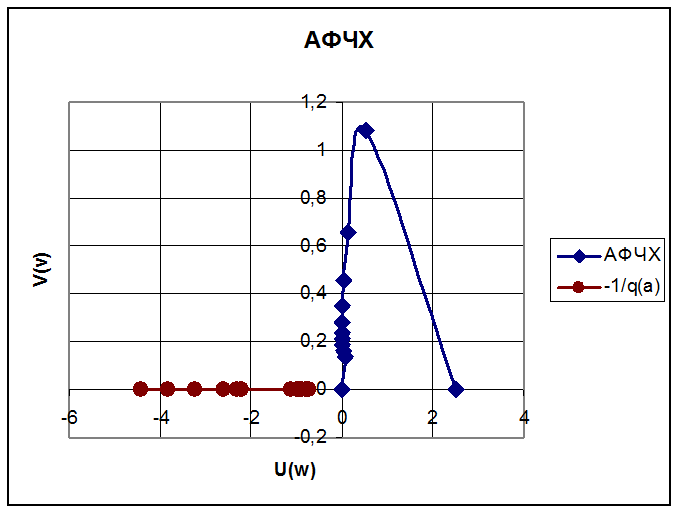
Рисунок 4 – Определение периодического решения и его
устойчивости
Периодического решения нет.
Вывод
Поскольку метод гармонической линеаризации является приближенным, то отсутствие решений уравнения гармонического баланса (точек пересечения характеристик линейной и нелинейной частей нет) означает, что используемый метод не позволяет выделить периодических движений у исследуемой системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.