Сложное напряженное состояние: Методическое пособие по курсу сопротивления материалов

Министерство общего и специального образования РФ

Московский  Государственный Технический Университет

им.Н.Э.Баумана

Калужский филиал


Е.И. Мосиянова, В.В. Кулибаба

СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ


Методическое пособие 
по курсу сопротивления материалов
 

Калуга, 1998

    Методическое пособие разработано в соответствии с программой курса сопротивления материалов для студентов машиностроительных специальностей.       

     Рассмотрено и одобрено на заседании кафедры К5-КФ “Сопротивление материалов” 15 октября 1998 г. (Протокол N 63).

     Утверждено 21 октября 1998 г. на заседании методической комиссии КФ МГТУ им. Н.Э.Баумана (Протокол N 1).

        Рецензент:  к.т.н. Сероштан В.И.

       Методическое пособие посвящено изложению курса сопротивления материалов применительно к вопросам сложного напряженного состояния элементов широкого класса машиностроительных конструкций.

        Рассмотрены примеры определения эквивалентных напряжений и коэффициентов запаса для трехмерного напряженного состояния, ломаного стержня, тонкостенных оболочек, тонкостенных труб, конических и цилиндрических резервуаров с жидкостью.

        Предлагаемый материал может быть использован в качестве электронного пособия на персональных ЭВМ в среде WINDOWS.

                                                  Содержание

                                                                                                       стр.

    1. Основные положения                                                            4

    2. Критерии пластичности                                                        5

    3. Примеры определения эквивалентных напряжений
        и коэффициентов запаса                                                       6

    4. Тонкостенные оболочки                                                      16

    5. Список литературы                                                              29

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ

     При расчете на прочность элементов конструкций необходимо знать допустимость того или иного состояния материала в отдельных их точках, называемых опасными.

     Материал конструкции в зависимости от условий нагружения может находиться в различных механических состояниях. При небольших внешних силах возникают только упругие деформации, или, как говорят, материал находится в упругом состоянии. При больших силах обнаруживаются заметные остаточные деформации и материал находится в пластическом состоянии. При дальнейшем увеличении нагрузки происходит образование местных трещин и наступает состояние разрушения.

     Механическое состояние материала в точке зависит в первую очередь от напряженного состояния в этой точке, хотя и не определяется им полностью. Задача заключается в том, чтобы установить меру напряженного состояния, по достижении которой происходит переход от упругого состояния к пластическому, и условий, при которых начинается разрушение, т. е. выработать критерий пластичности и критерий разрушения.

     Более разработанными, определенными и сравнительно более простыми являются критерии пластичности.

     При одноосном растяжении пластичного материала условием перехода из упругого состояния в пластическое является равенство  s=syt.

     При таком подходе для каждого случая сложного напряженного состояния материала (с произвольным соотношением  s1;s2 и s3) необходимо провести свои испытания для определения переходной точки. Такой подход требует огромного количества испытаний и технически сложен  в проведении этих испытаний. Но, если увеличивать пропорционально все компоненты напряженного состояния, т. е. изменять его подобным образом, то состояние материала изменится: либо возникнут пластические деформации, либо начнется разрушение. (Число, показывающее, во сколько раз следует увеличить все компоненты напряженного состояния, чтобы изменилось механическое состояние материала, называется коэффициентом запаса при сложном напряженном состоянии.) Таким образом, как при простом, так и при сложном напряженных состояниях можно достигнуть состояния равноопасности. Если теперь уменьшить эти напряжения в одинаковое число раз, то равноопасность сохранится.

     Если в двух напряженных состояниях коэффициенты запаса равны, то такие напряженные состояния называются равноопасными.

     Для заданного материала сравнение напряженных состояний можно производить не по коэффициенту запаса, а по числовой характеристике какого-либо одного напряженного состояния, выбираемого в качестве эталона .За такой эталон (эквивалент) удобнее всего принять напряжение обычного растяжения.

     Эквивалентное напряжение  - это такое напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасно с заданным сложным напряженным состоянием.

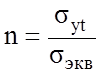
2. КРИТЕРИИ ПЛАСТИЧНОСТИ

    При определении критерия пластичности необходимо решить, какое из напряжений или какая их комбинация в сложном напряженном состоянии определяет переход материала к пластическому состоянию, которое далее будем называть предельным.

     Из существующих гипотез предельного состояния в настоящее время в технических расчетах используются три.

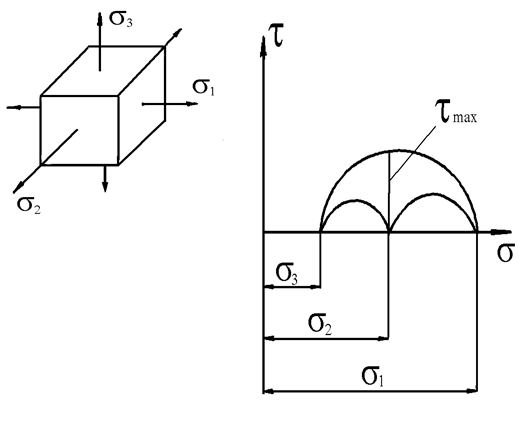
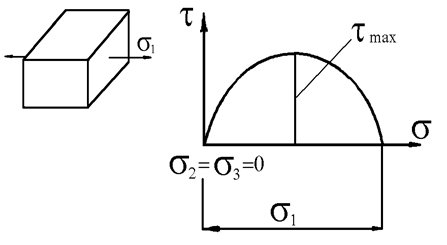
2.1 Гипотеза наибольших касательных напряжений.

     Два напряженных состояния равноопасны, если наибольшие касательные напряжения в них равны.

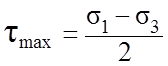
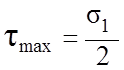
     Экспериментальная проверка показала, что для пластичных материалов эта гипотеза дает удовлетворительные результаты.

2.2 Гипотеза энергии формоизменения.

     Два напряженных состояния равноопасны, если их потенциальные энергии изменения формы равны.

          Сложное напряженное состояние               Одноосное растяжение

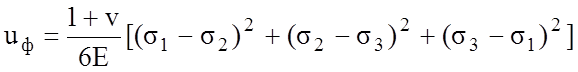
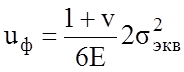
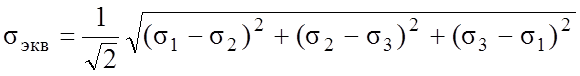
   Применима для пластичных материалов.

2.3 Теория Мора.

     Теория Мора основана на построении кругов Мора и не учитывает влияние . Как показывают экспериментальные данные, погрешность не превышает 15%. Однако, это единственная гипотеза, учитывающая, что предел текучести при растяжении  далеко не всегда равен пределу текучести при сжатии  и позволяющая оценивать прочность хрупких материалов.

                               sэкв =s1+ks3 , где

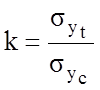      для пластичных и малопластичных материалов и