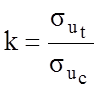 для хрупких
материалов.
для хрупких
материалов.
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ЭКВИВАЛЕНТНЫХ НАПРЯЖЕНИЙ
И КОЭФФИЦИЕНТОВ ЗАПАСА.
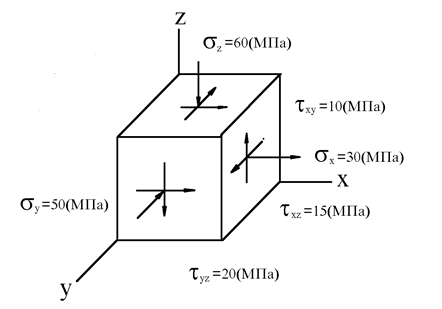
Пример 1.
 |
 |
||
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим первый случай напряженного состояния.
Главные напряжения определяем с помощью уравнения, записанного в инвариантной форме.
![]() , где
, где
![]()
![]()
 |
Для решения кубического уравнения используем подстановку:
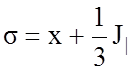 , тогда
, тогда ![]() , где
, где
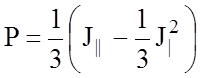 и
и 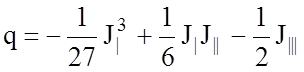
Все
три корня кубического уравнения действительные числа, если дискриминант
![]() . Для реальных напряженных состояний
Д всегда меньше 0, т.к. главные напряжения могут быть только
действительными величинами. В этом случае
. Для реальных напряженных состояний
Д всегда меньше 0, т.к. главные напряжения могут быть только
действительными величинами. В этом случае
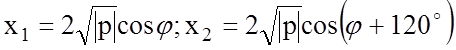 ;
;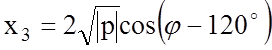
|p| - абсолютное значение коэффициента p, а
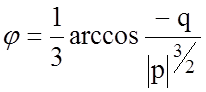
Определяем инварианты напряженного состояния.
![]()
![]()
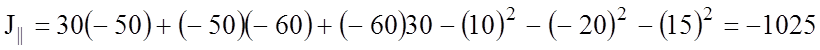
![]()
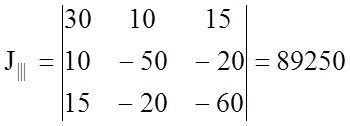
![]()
Находим коэффициенты p и q
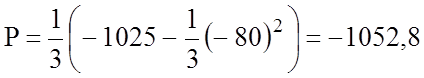
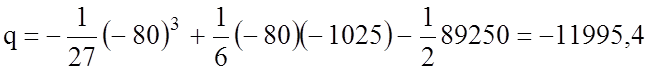
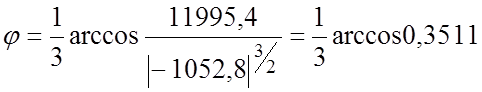

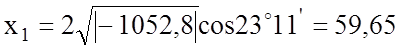
![]()
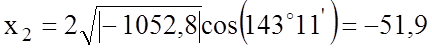
![]()
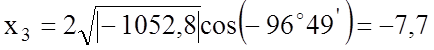
![]()
Окончательно получаем:
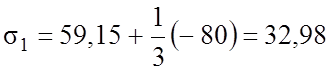
![]()
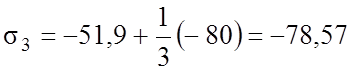
![]()
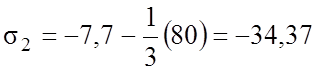
![]()
Так
как ![]() , для
определения эквивалентных напряжений используем теорию Мора:
, для
определения эквивалентных напряжений используем теорию Мора:
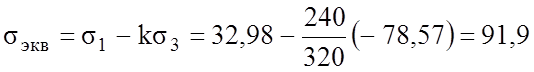
![]() ;
;
Соответственно коэффициент запаса будет равен:
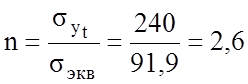
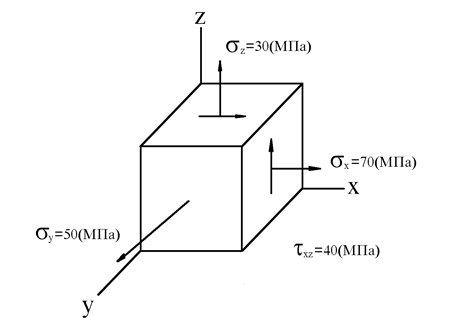
Рассмотрим второй случай напряженного состояния.
Площадка, пересекающая ось y, является
главной, соответственно ![]() (МПа) - главное напряжение.
(МПа) - главное напряжение.
Определим два других главных напряжения:

![]()
![]()
![]()
![]()
Получаем: ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]()
Так как пределы текучести при растяжении и статии равны, можно использовать как гипотезу наибольших касательных напряжений,, так и гипотезу формоизменения.
По гипотезе наибольших касательных напряжений:
![]()
![]()
По гипотезе формоизменения:
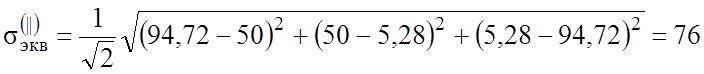
![]()
Соответственно коэффициенты запаса равны
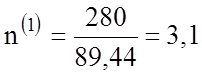 и
и 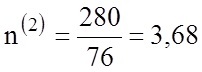
и имеет один порядок.
На основании выполненных расчетов можно сказать, что первое напряженное
состояние более опасно.
Пример 2.
В поперечном сечении бруска возникают следующие внутренние силовые факторы:
изгибающий момент в вертикальной плоскости ![]() ; изгибающий
момент в горизонтальной плоскости
; изгибающий
момент в горизонтальной плоскости ![]() ; крутящий
момент
; крутящий
момент ![]() . Сечение может быть выполнено в виде
круга, прямоугольника
. Сечение может быть выполнено в виде
круга, прямоугольника  ;
квадрата или трубчатого профиля
;
квадрата или трубчатого профиля ![]() .
.
Найти
наиболее рациональный вариант сечения, если F=500 н; l=20 см; ![]() МПа.
МПа.
Рассмотрим первый вариант сечения – круг диаметром d.
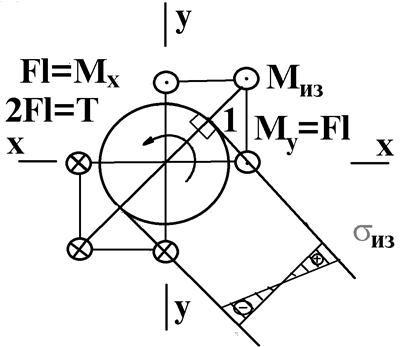
![]() ;
; ![]() .
.
Опасная точка рассматриваемого сечения – точка 1 –
лежит в плоскости действия суммарного момента. Изгиб происходит вокруг оси,
перпендикулярной этой плоскости и проходящей через центр тяжести сечения. ![]() ;
; ![]() .
.
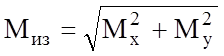 ;
;  ;
;
![]()
Подставляя значения, получаем:
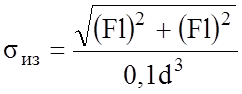
Касательные напряжения, возникающие от действия крутящего момента T, достигают в точке 1 максимального значения:
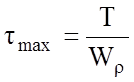 ;
; ![]()
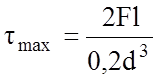
Выделим в окрестностях точки 1 элемент и проанализируем его напряженное состояние.
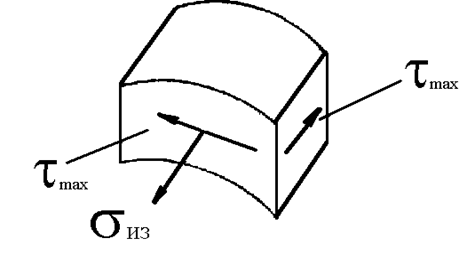 Одна из площадок рассматриваемого элемента свободна от
действия касательных напряжений, следовательно, является
главной. Нормальные напряжения на ней также отсутствует, что характерно
для плоского напряженного состояния.
Одна из площадок рассматриваемого элемента свободна от
действия касательных напряжений, следовательно, является
главной. Нормальные напряжения на ней также отсутствует, что характерно
для плоского напряженного состояния.
По другой площадке действуют только касательные напряжения; на третьей площадке имеют место и нормальные, и касательные напряжения.
Такое распределение напряжений характерно для плоского напряженного состояния.
Так как по условиям задачи механические характеристики материала не оговорены, можно воспользоваться гипотезой наибольших касательных напряжений.
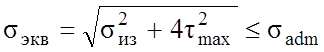
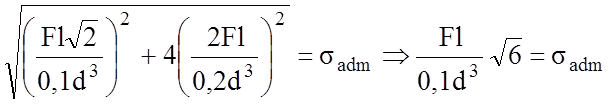
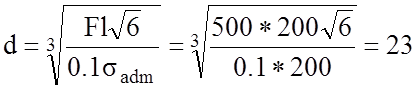 (мм)
(мм)
Минимально необходимый диаметр бруса составляет 23 мм.
Рассмотрим второй вариант сечения – прямоугольное.
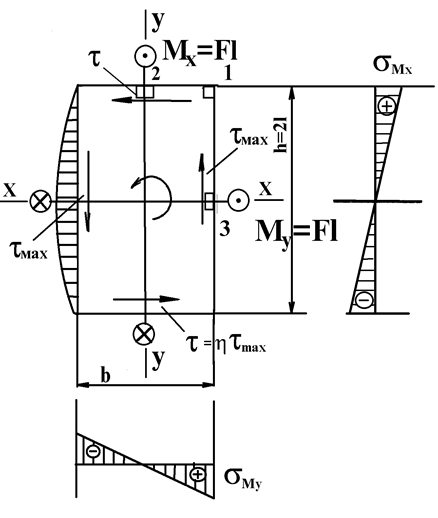 Из эпюр распределения напряжений видно, что
наиболее опасными являются точки 1, 2 и 3.
Из эпюр распределения напряжений видно, что
наиболее опасными являются точки 1, 2 и 3.
Изгибающий момент ![]() вызывает
в точках 1 и 2 напряжения
вызывает
в точках 1 и 2 напряжения
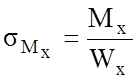 , где
, где 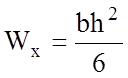
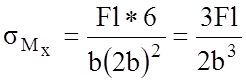
Изгибающий момент ![]() вызывает
в точках 1 и 3 напряжения
вызывает
в точках 1 и 3 напряжения
 , где
, где 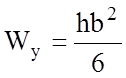
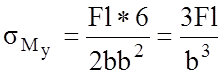
Крутящий
момент T вызывает максимальные касательные напряжения посередине
широкой грани (точка 3) 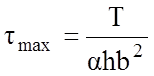 , где
, где
![]() зависит от отношения
зависит от отношения ![]() .
При
.
При ![]() =2
a=0,246
=2
a=0,246
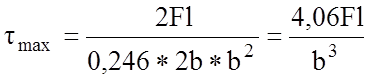
Напряжение
посeредине узкой грани (точка 2) будет меньше t=htmax (h зависит от ![]() и равно 0,795 )
и равно 0,795 )
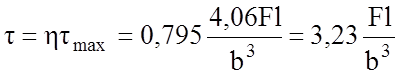
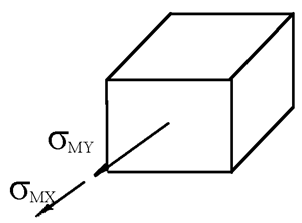
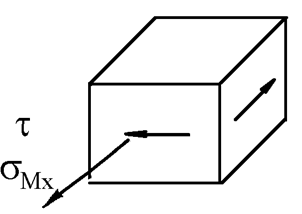
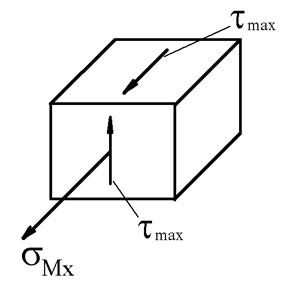
Выделим в окрестностях точек 1, 2 и 3 элементы и исследуем их напряженное состояние.
 |
 |
 |
|||
Напряженное состояние в точке 1 является линейным.
![]()
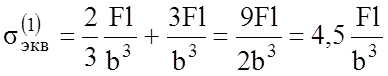
Напряженное состояние в точках 2 и 3 – плоское.
Точка
2. 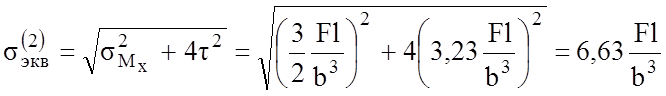
Точка
3 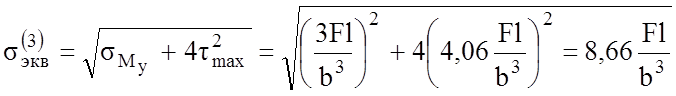
Таким образом, наиболее опасной является точка 3.
Из условия ![]() определяем размеры поперечного
сечения.
определяем размеры поперечного
сечения.
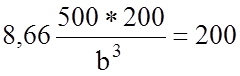
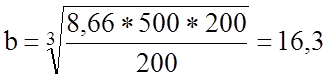 (мм)
(мм)
![]() (мм)
(мм)
Рассмотрим третий вариант сечения – квадрат.
Для квадрата 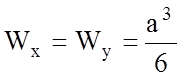 ,
где a – сторона квадрата.
,
где a – сторона квадрата.
Характер распределения напряжений по сечению аналогичен предыдущему случаю, но т.к.
![]() , то
, то 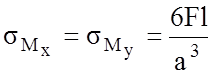
Касательные напряжения посередине всех четырех сторон одинаковы
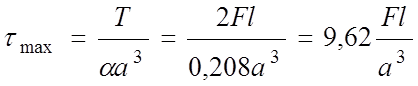
(при ![]() =1 a=0,208)
=1 a=0,208)
Точки 1, 2, и 3 расположены аналогично предыдущему случаю. Т.к. напряженные состояния в точках 2 и 3 полностью совпадают, ограничимся рассмотрением точек 1 и 2.
Точка 1
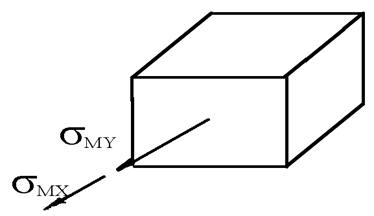
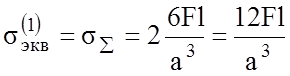
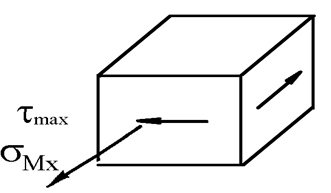
точка 2
 |
Точка
2 находится в более опасном состоянии. ![]()
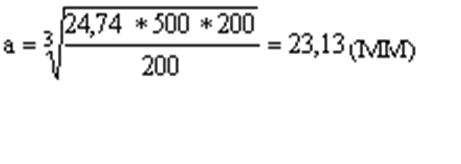
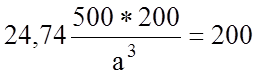
Рассмотрим четвертый вариант сечения – тонкостенную трубу.
 Трубчатое сечение, как и круглое
рассчитывается на изгиб от действия равнодействующего момента.
Трубчатое сечение, как и круглое
рассчитывается на изгиб от действия равнодействующего момента. ![]()
Касательные напряжения считаются равномерно распределенными по толщине стенки.
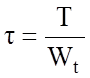 , где
, где ![]() ;
; 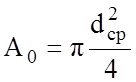
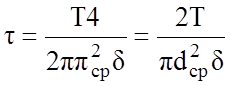 , выполняя подстановку получаем:
, выполняя подстановку получаем:
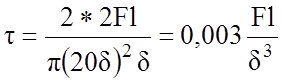
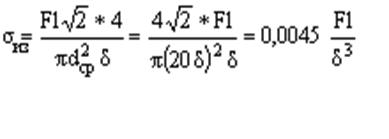 |
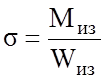
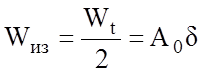
Рассмотрим напряженное состояние в точке 1.
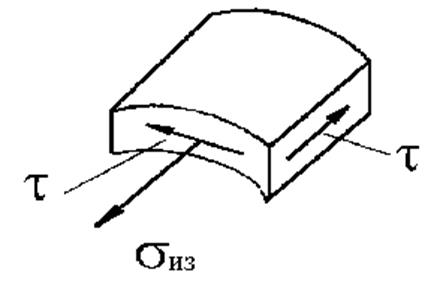 |
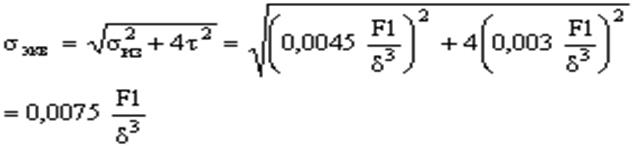 |
||
![]()
Определяем
толщину стенки ![]()
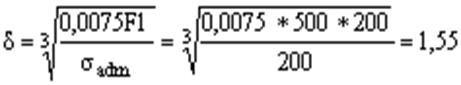
(мм)
![]() (мм)
(мм)
Сопоставим полученные результаты. Наиболее рациональным будет брус наименьшего веса.
Вес ![]() , где
, где
![]() - плотность, A –
площадь поперечного сечения, L
– длина, g – ускорение
свободного падения.
- плотность, A –
площадь поперечного сечения, L
– длина, g – ускорение
свободного падения.
Будем все сравнивать с брусом круглого поперечного сечения.
Круглое сечение:

(Н)
Прямоугольное сечение:
![]() (Н)
(Н)
Квадратное сечение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.