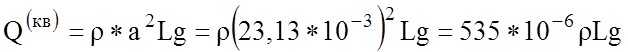 (Н)
(Н)
Трубчатое сечение:
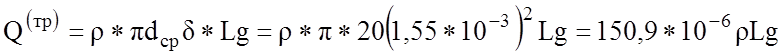 (Н)
(Н)
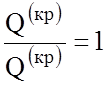
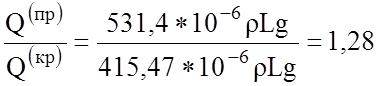
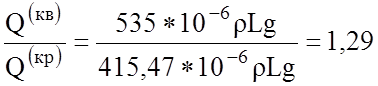
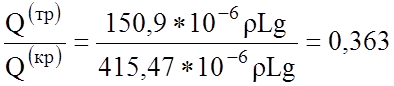
Таким образом, наиболее рациональным является трубчатое сечение.
4. ТОНКОСТЕННЫЕ ОБОЛОЧКИ
4.1.ТОНКОСТЕННЫЕ ОБОЛОЧКИ, НАХОДЯЩИЕСЯ ПОД
ДЕЙСТВИЕМ ПОСТОЯННОГО ДАВЛЕНИЯ.
Особенностью расчета тонкостенных оболочек по
безмоментной теории является основное допущение о том, что напряжение по
толщине оболочки считается постоянным, а напряженное состояние – плоским.
Расчет ведется по срединной поверхности. Исключением является случай, когда
оболочка находится под действием внешнего и внутреннего давлений.
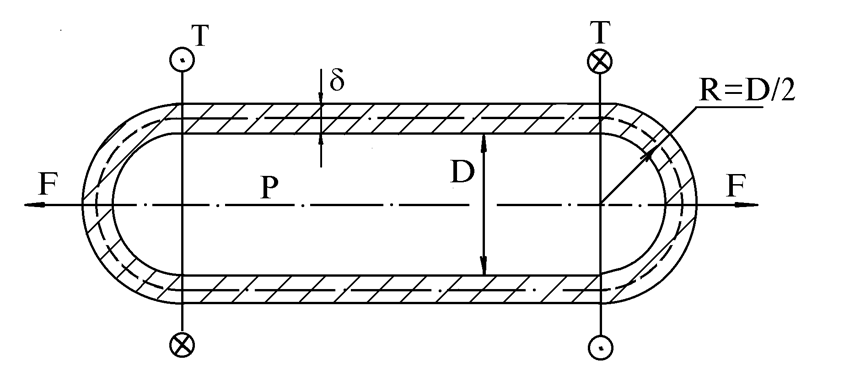
Пример 1.
Тонкостенная
оболочка со сферическими днищами (D=80мм; δ=4мм.) находится под
действием внутреннего давления Р=5Мпа; продольной нагрузки F=15,7кн
и скручивающих моментов Т=2 кнм Оболочка изготовлена из стали 40ХН, имеющей
предел текучести при растяжении 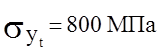 , а предел текучести
при сжатии
, а предел текучести
при сжатии 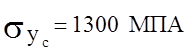 . Определить коэффициент запаса.
Расчет выполнить для участка достаточно удаленного от днищ.
. Определить коэффициент запаса.
Расчет выполнить для участка достаточно удаленного от днищ.
Задачу решаем, используя принцип независимости действия сил. Сложное нагружение оболочки можно разложить на три простых:
а) - оболочка находится только под действием внутреннего давления; б) - оболочка растягивается;
в) – оболочка скручивается.
а). Для определения напряжений возникающих от действия давления, используем уравнение Лапласа и уравнение равновесия.
Под
действием давления Р оболочка растягивается в продольном и окружном
направлениях. Соответственно в ней возникают напряжения: ![]() -меридиональное напряжение (возникает
в продольном направлении) и
-меридиональное напряжение (возникает
в продольном направлении) и ![]() -окружное
напряжение (действует в окружном направлении).
-окружное
напряжение (действует в окружном направлении).
Уравнение
Лапласа 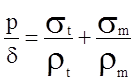 содержит два неизвестных
содержит два неизвестных ![]() и
и ![]() (
(![]() -радиус в окружном направлении,
-радиус в окружном направлении, ![]() - радиус в меридиональном
направлении).
- радиус в меридиональном
направлении).
В
нашем случае, для сечений достаточно удаленных от днищ ![]() (стенки
сосуда параллельны друг другу).
(стенки
сосуда параллельны друг другу).
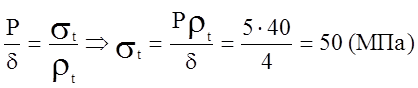 .
.
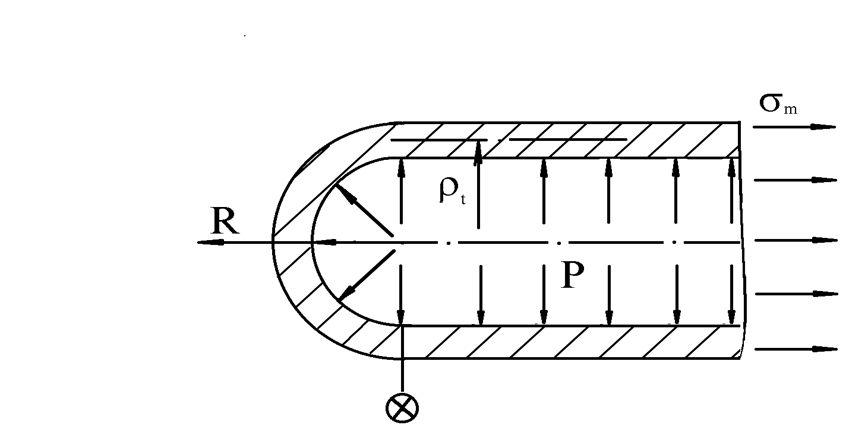
Для определения меридиональных напряжений составим
уравнение равновесия
![]() .
.
Согласно
теореме о равнодействующей давления, проекция равнодействующей давления на
какую-либо ось всегда равна произведению давления на площадь проекции
поверхности, воспринимающей давление на плоскость, нормальную к этой оси: 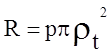 .
.
Это
усилие вызывает в поперечном сечении оболочки ( ![]() )
напряжения
)
напряжения ![]() .
.
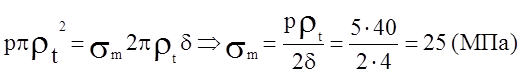
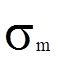 |
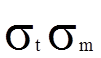 |



 Напряженное
состояние во всех точках поперечного сечения одинаково.
Напряженное
состояние во всех точках поперечного сечения одинаково.
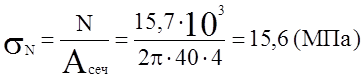 |
 |
 |



N -продольная растягивающая сила , равная F.
Напряженное состояние во всех точках поперечного сечения одинаково.
b). Скручивающий момент Т вызывает в поперечном сечении касательные напряжения τ
.
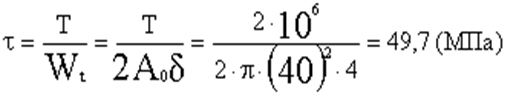 |
Wt-момент
сопротивления при кручении тонкостенного круглого профиля уже был рассмотрен
ранее ( 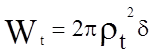 ).
).

Напряженное состояние во всех точках поперечного сечения одинаково.
Рассмотрим суммарное воздействие этих сил.
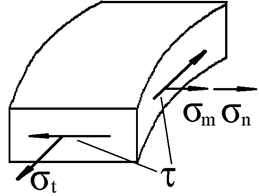 Напряженное состояние стенки оболочки
Напряженное состояние стенки оболочки
является плоским.
.
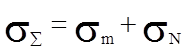 |
Так как материал имеет разные пределы текучести при растяжении и сжатии, используем теорию Мора:
sэкв=s1-ks3
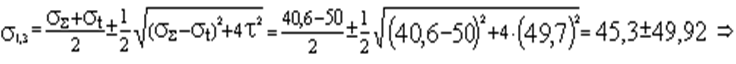 |
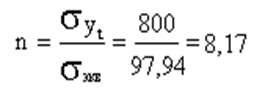
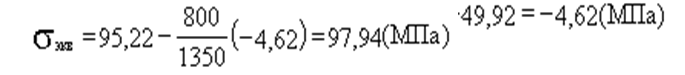 |
Коэффициент запаса равен:.
Для сосудов, находящихся под давлением, рекомендуемый коэффициент запаса составляет(5…15).
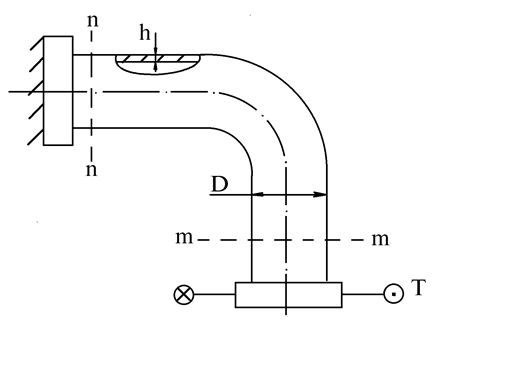
Пример 2.
Тонкостенная трубка находится под действием давления Р. На ее конус приложен крутящий момент T=РD3.
В
какой точке сечений m-m и n-n напряженное состояние будет наиболее опасным, если 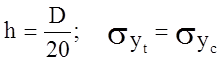 .
.
![]()
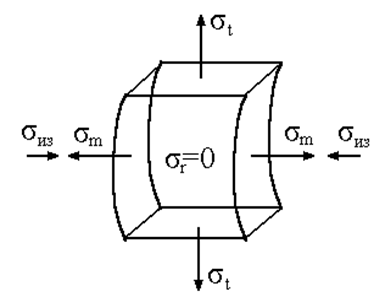
![]() Рассмотрим
сечение m-m. Все точки этого
сечения находятся в одинаковом напряженном состоянии, испытывая нормальные
напряжения (меридиональные и окружные) от давления Р и касательные напряжения
от действия крутящего момента T.
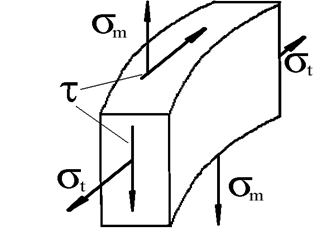
Рассмотрим
сечение m-m. Все точки этого
сечения находятся в одинаковом напряженном состоянии, испытывая нормальные
напряжения (меридиональные и окружные) от давления Р и касательные напряжения
от действия крутящего момента T.
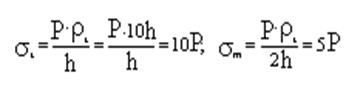 |
 .
.
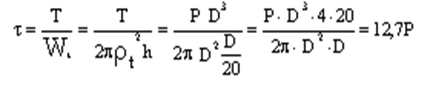 |
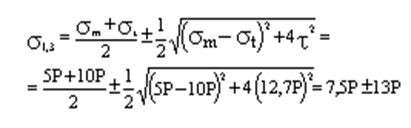 |
Определяем главные напряжения:
Рассмотрим сечение n-n.
Меридиональные и окружные напряжения в этом сечении такие же, как и в предыдущем случае.
Крутящий момент T для сечения n-n превращается в изгибающий момент.
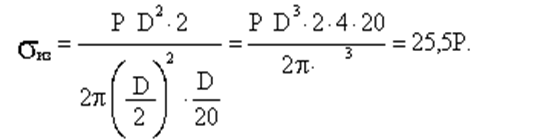 |
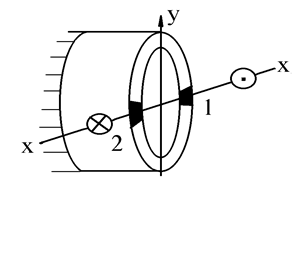 В точке 1 должны возникнуть напряжения
растяжения, а в точке 2 –сжатия.
В точке 1 должны возникнуть напряжения
растяжения, а в точке 2 –сжатия.
Точка 1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Напряженное
состояние является плоским. ![]()
(радиальные напряжения не учитываются sr=0).
![]()
![]()
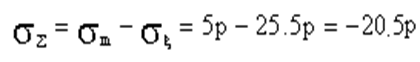 |
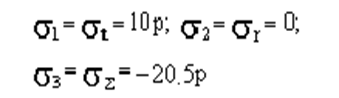 |
|||
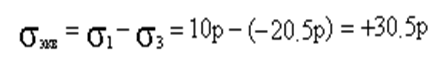 |
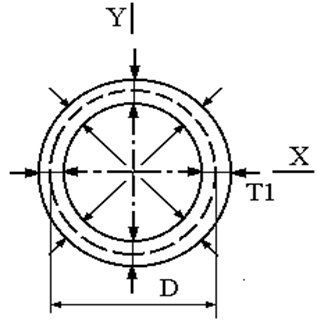
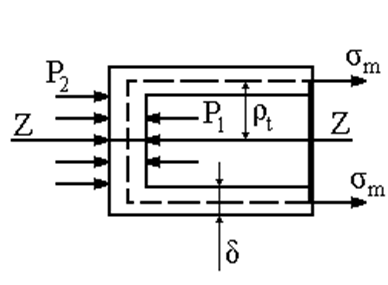
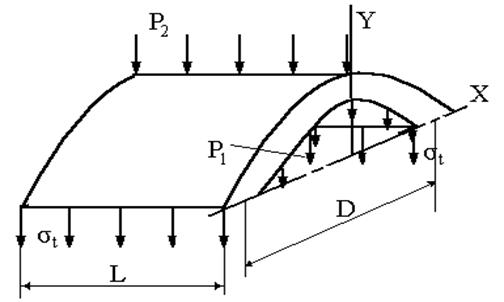
Пример 3. Исследоватьнапряженное состояние тонкостенной трубки и определить коэффициент запаса nт. Расчет вылолнить для сечения, достаточно удаленное от концов трубки. Материал – сталь 50.
|
|
|


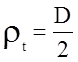 |
 |
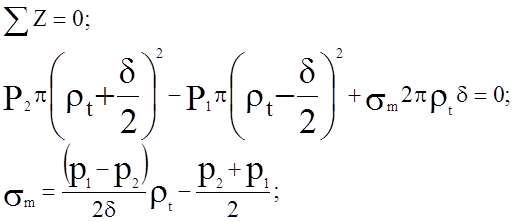 |
||
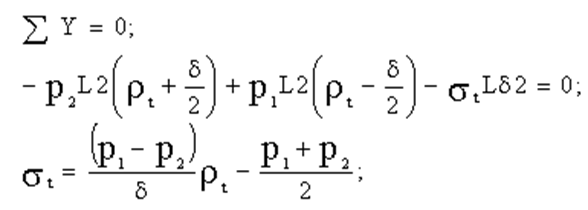 |
|
|||||||
|
|||||||
|
|||||||
|
|
||||||
 |
 |
||
Точка на наружней Точка на внутренней поверхности поверхности.
во втором случае по модулю больше, чем в первом, поэтому
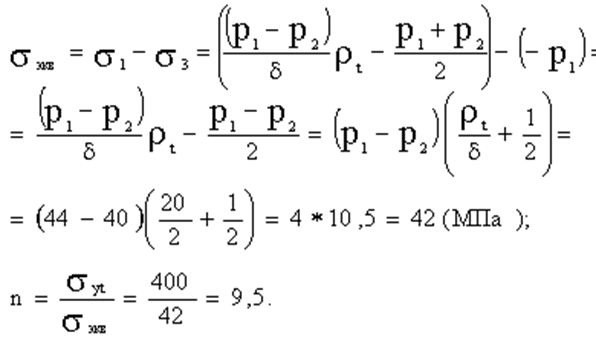 |
Пример 4. Конический резервуар с постоянным внутренним давлением и постоянной толщиной стенки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.