s1= 0, s2= 4×3 - 2×32 + 33 = 9 м. Тогда <u> = 9 / 3 = 3м/с
Среднее ускорение < a> определяется соотношением < a> = Du / Dt, где Dt = 3 с, а Du = u2 –u1. Скорость для моментов времени t2 и t1 определим из выражения u(t) = s¢= 4 - 4t + 3t2, при t1=0 u1=4 м/с, при t2= 3 с u2= 19 м/с, тогда < a> = (19 – 4) / 3 = 5 м/с2.
Пример 2. На рис. 10 показана зависимость скорости от времени для нескольких движений (1, 2, 3). Дать характеристику каждому движению по схеме: тип движения (равномерное, равнозамедленное, равноускоренное); начальная скорость u0; ускорение a; путь, пройденный телом за все время движения.
Р е ш е н и е. На графике 1 представлено равнозамедленное движение, его начальная скорость u0 равна 12 м/с, ускорение определяем по формуле a =( u - u0)/Dt . Вычисляем:
a = ( 0 - 12) / 6 = -2 м/с2.
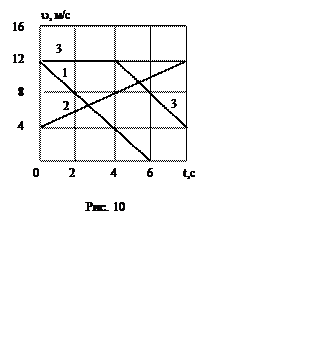 |
Путь можно найти двумя способами - по формуле ( 12 ), все данные для которой берем из графика:
s1= 12×6 - 2×62/2 = 36 м,
или через площадь треугольника под линией зависимости u(t)
s1= 12 × 6 / 2 = 36 м.
График 2 соответствует равноускоренному движению с начальной скоростью u0 = 4 м/с. Через 8 с после начала движения скорость возросла до 12 м/с (конечная скорость u), тогда ускорение
a = ( 12 - 4) / 8 = 1 м/с2.
Путь определяем по формуле (12)
s2 = 4 × 8 + 1×82/2 = 64 м.
Очевидно, что площадь трапеции под графиком 2 равна тоже 64 м.
График 3 показывает, что движение в течение первых четырех секунд было равномерным со скоростью u = 12 / 3 = 4 м/с. В последующие четыре секунды движение равнозамедленное с начальной скоростью u0 = 4 м/с и конечной скоростью, равной 4 м/с. Ускорение при равнозамедленном движении
a = ( 4 - 12) / 4 = -2 м/с2.
Путь, пройденный за все время движения , определяется суммой пути равномерного движения sрвнм = u× t = 12 × 4 = 48 м и равнозамедленного sрзмдл= 12 × 4 – 2 × 16 / 2 =32 м.
Общий путь s = 48 + 32 = 80 м.
Пример 3. Колесо радиусом 10 см вращается так, что зависимость угла поворота радиуса колеса от времени задается уравнением j = 3 + 2t + t3 (j в радианах, время в секундах). Для точек на ободе колеса через три секунды после начала движения найти 1) угловой путь в радианах и оборотах; 2) угловую скорость и число оборотов в единицу времени; 3) линейную скорость; 4) угловое ускорение; 5) нормальное ускорение; 6) тангенциальное ускорение; 7) полное ускорение.
Р е ш е н и е. 1) Угловой путь в радианах найдем подстановкой времени в уравнение движения: j = 3 + 2×3 + 33 = 36 рад. Угловой путь j связан с оборотами N соотношением j = 2πN, т.е. N = j / 2π, отсюда N = 36/6,28 = 5,73 оборота.
2) Угловая скорость w = j¢ =2 + 2t2, для нашей задачи w =2 + 2×32= 20 рад/с. Угловая скорость связана с числом оборотов в единицу времени соотношением w = 2πn, отсюда n = 20 / 6.28 = 3,18 об/с.
3) Линейная скорость u = w×R, т.е. u = 20×0,1 = 2 м/с.
4) Угловое ускорение e = w¢ = 4t, т.е. e = 4×3 = 12 рад/с2.
5) Нормальное ускорение аn = u2/R = w2×R, т.е. аn =202×0,1= 40 м/с2.
6) Тангенциальное ускорение аt = du/dt = u¢ = e×R, т. е. аt = 12×0,1 = 1,2 м/с2.
![]() 7) Полное ускорение , , т.е.
7) Полное ускорение , , т.е.
а = Ö 402 + 1,22 = 40,02 м/с2.
Пример 4. Снаряд вылетел из орудия под углом 300 к горизонту со скоростью u0 = 600 м/с. Найти через 20с после начала движения 1) положение снаряда (на подъеме или спуске); 2) высоту подъема снаряда; 3) его скорость; 4) угол между нормальным и полным ускорением; 5) тангенциальное и нормальное ускорения. Принять g = 10 м/с2
А н а л и з. Траектория движения снаряда представлена на рис.2. Движение сложное, состоит из двух простых: вдоль оси Х оно равномерное с постоянной скоростью uх = u0х = u0×cosa , вдоль оси У - равнопеременное с начальной скоростью u0у= u0×sina и ускорением g= 9,8 м/с2. Запишем уравнения движения в проекциях на координатные оси:
ОХ: х = u0×cosa×t, (25)
ОУ: y = u0×sina×t – gt2/2, (26)
uу = u0×sina – gt. (27)
Знак «минус» в последних двух уравнениях показывает, что вектор gнаправлен против положительного направления оси ОУ(если бы ось ОУ направили вниз, знак изменился бы на противоположный).
Р е ш е н и е. 1) Для определения положения снаряда в указанный момент времени t = 20с нужно найти время движения снаряда до высшей точки траектории (обозначим это время, например, через t1). Если t будет меньше t1, снаряд будет подниматься, если наоборот – опускаться. Время t найдем из уравнения (27).
Поскольку в высшей точке траектории uу = u0×sina – g t1 = 0, то
t1 = u0×sina / g. t1 = 600×sin300 /10 = 600×0,5 /10 = 30 c.
Сравним t и t1, t < t1, значит снаряд находится на подъеме.
2) Через t=20 с после начала движения у = h. Определим h по уравнению ( 25 ): h = u0×sina×t – gt2/2;
h = 600×sin300×20 - 10×(20)2/2 = 6000 – 2000 = 4000 м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.