Кинематика. Материальная точка, система отсчета, траектория, путь, перемещение. Кинематика поступательного движения. Кинематика вращательного движения, страница 2

                                                 а = а_τ + а_n.                                                      (6)

        Тангенциальное (или касательное) ускорение  а_τ   характеризует быстроту изменения скорости по величине, его модуль

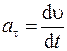                                                    .                                            (7)

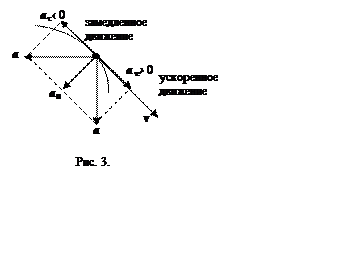
 Тангенциальное ускорение направлено по касательной к траектории движения по скорости при ускоренном движении и против скорости при замедленном движении  (рис. 3)..

        Нормальное  (центростремительное) ускорение а_n характеризует изменение скорости по направлению, его модуль

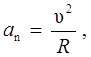                                                                                 (8)

где R -  радиус кривизны траектории.   

         Вектор нормального ускорения  направлен к центру окружности, которую можно провести касательно к данной точке траектории; он всегда  перпендикулярен вектору тангенциального ускорения  (рис.3).

         Модуль полного ускорения определяется по теореме Пифагора

                                           .                                                          (9)

        Направление вектора полного ускорения  а определяется векторной суммой векторов нормального и тангенциального ускорений (рис.3)

 

        Равнопеременным называют движение с постоянным ускорением. Если ускорение положительно, то это  равноускоренное движение, если же оно отрицательно - равнозамедленное.

       При прямолинейном движении  а _ם = 0 и  а = а_τ. Если а _ם= 0 и   а_τ = 0, тело движется прямолинейно и равномерно;  при а _ם= 0 и   а_τ = const движение прямолинейное равнопеременное .

      При равномерном движении пройденный путь вычисляется по формуле:

                              ds = udt → s  = ∫udt = u∫dt = ut + s₀,                             (10 )

где  s₀ - начальный путь для  t = 0.  Последнюю формулу необходимо запомнить.

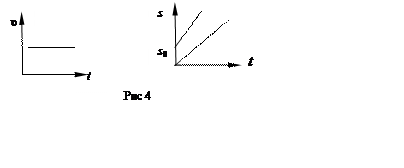
Графические зависимости υ(t) и s(t) приведены на рис .4.

 

Для равнопеременного движения    u = ∫а dt= а∫ dt, отсюда

                                                   u= аt+ u₀,                                             (11)

где  u₀  - начальная скорость при  t=0.                                                                                                                        

        Пройденный путь   s= ∫udt = ∫(аt+ u₀)dt.  Решая этот интеграл, получим

                                              s =  аt²/2 + u₀t +s₀,                                    (12)

где s₀ - начальный путь (для t = 0).  Формулы (11), (12) рекомендуем запомнить.

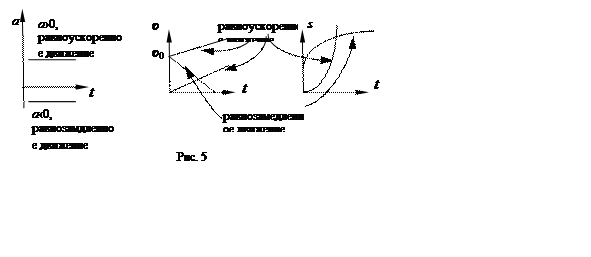
        Графические зависимостиа(t), υ(t) и s(t) приведены на рис .5.

 

        К равнопеременному движению с ускорением свободного падения   g = 9,81 м/с² относится свободное движение тел в вертикальной плоскости: вниз тела падают с g› 0,  при движении вверх ускорение  g‹ 0. Скорость движения и пройденный путь при этом изменяется согласно  (11):

                                              u= u₀ + g t;       (13)

                                          h  =   gt²/2 + u₀t + h ₀.                                         (14)

        Рассмотрим движение тела, брошенного под углом к горизонту (мяч, камень, пушечный снаряд,… ). Это сложное движение состоит из двух простых: по горизонтали вдоль оси ОХ и вертикали вдоль оси ОУ (рис.6).  По горизонтальной оси  в отсутствие сопротивления среды движение равномерное; по вертикальной оси  - равнопеременное: равнозамедленное до максимальной точки подъема  и равноускоренное после нее. Траектория движения имеет вид параболы. Пусть u₀ - начальная скорость тела, брошенного под углом  α  к горизонту из точки А (начало координат).  Ее  составляющие по выбранным осям:

                                  u_0x = u_x = u₀ cos α  = const;                                        (15)

                                  u_0у = u₀ sinα.                                                               (16)

 

                                     Рис. 6.

Согласно формуле  (13) имеем для нашего примера в любой точке траектории до точки С

                      u_у = u_0у - g t  = u₀ sinα. - g t ;                                                

                      u_х = u_0х  = u₀ cos α  = const.                                                   

        В наивысшей точке траектории, точке С, вертикальная составляющая скорости u_у = 0. Отсюда можно найти время движения до точки С:

            u_у = u_0у - g t  = u₀ sinα. - g t= 0 →  t= u₀ sinα/ g.                           (17)

Зная    это   время,   можно  определить  максимальную  высоту  подъема тела  по (14):

  h_max= u_0уt- gt²/2=u₀ sinα u₀ sinα/g – g(u₀ sinα /g)²/2 = (u₀ sinα)²/(2g)       (18)

        Поскольку траектория  движения симметрична, то полное  время движения  до конечной точки  В  равно

                                        t₁ =2 t = 2u₀ sinα / g.                                       (19)

Дальность полета АВ  с учетом  (15)  и  (19) определится так:

                     АВ = u_х t₁ = u₀ cosα 2u₀ sinα/ g = 2u₀²cosα sinα/ g.          (20)

     Полное ускорение движущегося тела в любой точке траектории равно ускорению свободного падения  g ; его можно разложить на нормальное и тангенциальное, как было показано на рис.3.

3.  Кинематика вращательного движения