Кинематика. Материальная точка, система отсчета, траектория, путь, перемещение. Кинематика поступательного движения. Кинематика вращательного движения, страница 3

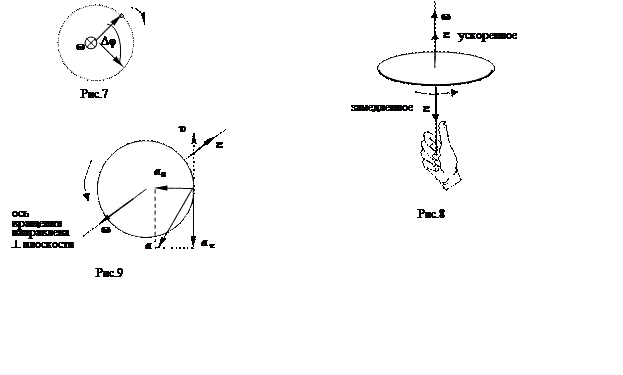
    Вращательнымназывается движение, при котором все точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения. Пусть точка движется по окружности радиуса R в указанном  направлении  (рис.7). Ее положение  через  время   Δt  можно задать   углом   Δφ (угловым путем), измеряемым  в  системе СИ в радианах (рад).

    Вектор угловой скорости ω характеризует быстроту  направление вращения. Средней угловой скоростью движения в интервале времени Δtназывают величину

                                       ,                                            (21)

где  Δφ - угловой путь, пройденный за это время.

    Мгновенной угловой скоростью  движения называют величину

                                                                         (22)

Единица измерения угловой скорости - рад/с. Направление вектора угловой скорости определяется правилом правого винта (правилом правого буравчика).    Угловая скорость направлена вдоль оси вращения по поступательному движению острия правого винта (буравчика), если его головку поворачивать по направлению вращения тела. В нашем случае  вектор ω направлен перпендикулярно плоскости чертежа  «от нас». Это обозначается на чертеже значком         (рис.7, 8). Если бы  ω был направлен к нам, он бы обозначался значком

    Угловое ускорение eпоказывает, как меняется скорость вращения со временем, измеряется в СИ в рад/с²

    Среднее  угловое  ускорение  

                                            ,                                      (23) 

    Мгновенное угловое ускорение определяетсякак производная угловой скорости по времени:

                                                                           (24)

Угловое ускорение направлено  (рис. 8, 9) вдоль оси вращения по угловой скорости, если вращение ускоренное (ε › 0) и против нее, если вращение замедленное (ε ‹ 0).

 

 

 

 

 

           

                    .

          Угловые характеристики вращающейся точки w  и   e связаны с ее линейными характеристиками   υ,a_n и  a_t :

                          u = wR;     a_n = w²R;       a_t = eR .                                            (24)     

Здесь R - радиус вращения. На рис. 9 показаны вектора всех вышеназванных величин для замедленного движения.

    Если  угловая скорость остается постоянной величиной (w=const, e= 0),  то вращение равномерное; при постоянном угловом ускорении (e =  const) - вращение равнопеременное. Расчетные формулы для этих видов движения аналогичны формулам при поступательном движении и приведены в таблице 1.

                                                                                                  Т а б л и ц а 1

            Сопоставление кинематических характеристик

              поступательного и вращательного движений

Поступательное движение	Вращательное  движение
s – путь, м	j - угловой путь, рад j = 2pN;      (N – обороты)
u -  -скорость ( м/с) u = ds/dt = s¢	w- угловая скорость, рад/с  w = 2pn;       w =dj/dt = j¢                        (n – об/с)
a - ускорение, м/с2 a = du/dt = u¢	e - угл. ускорение, рад/с2 e = dw/dt = w¢
Неравномерное движение
<u>=Ds/Dt <a>=Du/Dt		<w>=DjDt <e>=Dw/Dt
Равномерное    движение
u -const s = ut	w - const j = wt
Равнопеременное   движение
a = Du/Dt  прямолинейное s = u0t ± at2/2 u = u0 ± at	e = Dw/Dt j = w0t ± et2/2 w = w0 ± et
Криволинейное движение
a n= u2/R a t   = du/dt a  = Ö a t2 + a n2

Равномерное вращение  можно характеризовать периодом вращения Т - временем, за которое совершается один полный оборот, т. е.  поворачивается на угол 2π. Тогда  w = j/ t = 2π./Т или 

                                          Т  = 2π./ w.

Графические зависимости j(t), w(t), e(t) для вращательного движения имеют такой же вид, как и для поступательного (рис.4, 5).

   Далее приведены примеры решения задач по кинематике.

4.    Примеры решения задач

          Пример 1.    Уравнение зависимости пути s, пройденного телом,  от  времени   t  имеет  вид     s = 4t – 2t² + t³   (sв м,  tв с).   Найти: 1) зависимость скорости   u  и ускорения  а  от времени t;  2)  расстояние, пройденное телом, скорость и ускорение тела через три секунды после начала движения;  3)  среднюю скорость и среднее ускорение тела за первые три секунды движения.

          Р е ш е н и е.  1) Уравнение движения тела задано траекторным способом. Скорость в этом случае определяется как первая производная от пути по времени , т.е. по формуле ( 2  ), ускорение -  как вторая производная от пути по  времени или первая производная от скорости по времени, т.е.

                    u(t) = s¢= 4 - 4t + 3t²;       а(t) = u¢ = s¢¢ = -4 + 6t×

2)   Найдем путь, скорость и ускорение тела через три секунды после начала движения, подставив время в предыдущие уравнения:

 s =4×3 - 2×3² + 3³ = 9 м;    u = 4 - 4×3 + 3×3² = 10 м/с;   а = -4 + 6×3 = 14 м/с².×

3)     Средняя   скорость   движения   <u>   определяется   соотношением    <u> = Ds / Dt, где  Dt =  t₂ -t₁, Ds = s₂ –s₁. В нашем случае  t₁= 0, t₂= 3 с, Dt = 3 с;